Luogu P1081 NOIP2012开车旅行

Posted 2020-10-13

题目描述

小 A 和小 B 决定利用假期外出旅行，他们将想去的城市从 1 到 N 编号，且编号较小的城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 i 的海拔高度为Hi，城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值，即d[i,j] = |Hi− Hj|。 旅行过程中，小 A 和小 B 轮流开车，第一天小 A 开车，之后每天轮换一次。他们计划选择一个城市 S 作为起点，一直向东行驶，并且最多行驶 X 公里就结束旅行。小 A 和小 B的驾驶风格不同，小 B 总是沿着前进方向选择一个最近的城市作为目的地，而小 A 总是沿着前进方向选择第二近的城市作为目的地（注意：本题中如果当前城市到两个城市的距离相同，则认为离海拔低的那个城市更近）。如果其中任何一人无法按照自己的原则选择目的城市，或者到达目的地会使行驶的总距离超出 X 公里，他们就会结束旅行。

在启程之前，小 A 想知道两个问题：

1. 对于一个给定的 X=X0，从哪一个城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小（如果小 B 的行驶路程为 0，此时的比值可视为无穷大，且两个无穷大视为相等）。如果从多个城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值都最小，则输出海拔最高的那个城市。

2. 对任意给定的 X=Xi和出发城市 Si，小 A 开车行驶的路程总数以及小 B 行驶的路程总数。

输入输出格式

输入格式：

第一行包含一个整数 N，表示城市的数目。

第二行有 N 个整数，每两个整数之间用一个空格隔开，依次表示城市 1 到城市 N 的海拔高度，即 H1，H2，……，Hn，且每个 Hi都是不同的。

第三行包含一个整数 X0。

第四行为一个整数 M，表示给定 M 组 Si和 Xi。

接下来的 M 行，每行包含 2 个整数 Si和 Xi，表示从城市 Si出发，最多行驶 Xi公里。

 

输出格式：

输出共 M+1 行。

第一行包含一个整数 S0，表示对于给定的 X0，从编号为 S0的城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小。

接下来的 M 行，每行包含 2 个整数，之间用一个空格隔开，依次表示在给定的 Si和

Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。

输入输出样例

输入样例#1： 

4 
2 3 1 4 
3 
4 
1 3 
2 3 
3 3 
4 3

输出样例#1： 

1 
1 1 
2 0 
0 0 
0 0 

输入样例#2： 

10 
4 5 6 1 2 3 7 8 9 10 
7 
10 
1 7 
2 7 
3 7 
4 7 
5 7 
6 7 
7 7 
8 7 
9 7 
10 7

输出样例#2： 

2 
3 2 
2 4 
2 1 
2 4 
5 1 
5 1 
2 1 
2 0 
0 0 
0 0

说明

【输入输出样例 1 说明】

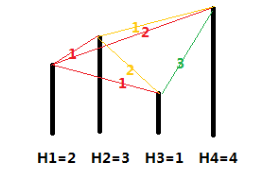
各个城市的海拔高度以及两个城市间的距离如上图所示。

如果从城市 1 出发，可以到达的城市为 2,3,4，这几个城市与城市 1 的距离分别为 1,1,2，但是由于城市 3 的海拔高度低于城市 2，所以我们认为城市 3 离城市 1 最近，城市 2 离城市1 第二近，所以小 A 会走到城市 2。到达城市 2 后，前面可以到达的城市为 3,4，这两个城市与城市 2 的距离分别为 2,1，所以城市 4 离城市 2 最近，因此小 B 会走到城市 4。到达城市 4 后，前面已没有可到达的城市，所以旅行结束。

如果从城市 2 出发，可以到达的城市为 3,4，这两个城市与城市 2 的距离分别为 2,1，由于城市 3 离城市 2 第二近，所以小 A 会走到城市 3。到达城市 3 后，前面尚未旅行的城市为4，所以城市 4 离城市 3 最近，但是如果要到达城市 4，则总路程为 2+3=5>3，所以小 B 会直接在城市 3 结束旅行。

如果从城市 3 出发，可以到达的城市为 4，由于没有离城市 3 第二近的城市，因此旅行

还未开始就结束了。

如果从城市 4 出发，没有可以到达的城市，因此旅行还未开始就结束了。

【输入输出样例 2 说明】

当 X=7 时， 如果从城市 1 出发，则路线为 1 -> 2 -> 3 -> 8 -> 9，小 A 走的距离为 1+2=3，小 B 走的距离为 1+1=2。（在城市 1 时，距离小 A 最近的城市是 2 和 6，但是城市 2 的海拔更高，视为与城市 1 第二近的城市，所以小 A 最终选择城市 2；走到 9 后，小 A 只有城市 10 可以走，没有第 2 选择可以选，所以没法做出选择，结束旅行）

如果从城市 2 出发，则路线为 2 -> 6 -> 7 ，小 A 和小 B 走的距离分别为 2，4。

如果从城市 3 出发，则路线为 3 -> 8 -> 9，小 A 和小 B 走的距离分别为 2，1。

如果从城市 4 出发，则路线为 4 -> 6 -> 7，小 A 和小 B 走的距离分别为 2，4。

如果从城市 5 出发，则路线为 5 -> 7 -> 8 ，小 A 和小 B 走的距离分别为 5，1。

如果从城市 6 出发，则路线为 6 -> 8 -> 9，小 A 和小 B 走的距离分别为 5，1。

如果从城市 7 出发，则路线为 7 -> 9 -> 10，小 A 和小 B 走的距离分别为 2，1。

如果从城市 8 出发，则路线为 8 -> 10，小 A 和小 B 走的距离分别为 2，0。

如果从城市 9 出发，则路线为 9，小 A 和小 B 走的距离分别为 0，0（旅行一开始就结

束了）。

如果从城市10出发，则路线为 10，小A 和小B 走的距离分别为0，0。

从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值都最小，但是城市 2 的海拔更高，所以输出第一行为 2。

对于30%的数据，有1≤N≤20，1≤M≤20；

对于40%的数据，有1≤N≤100，1≤M≤100；

对于50%的数据，有1≤N≤100，1≤M≤1,000；

对于70%的数据，有1≤N≤1,000，1≤M≤10,000；

对于100%的数据，有1≤N≤100,000，1≤M≤100,000，-1,000,000,000≤Hi≤1,000,000,000，0≤X0≤1,000,000,000，1≤Si≤N，0≤Xi≤1,000,000,000，数据保证Hi 互不相同。

 

Solution : 

居然还有人用倍增了??

显然每个点只会向标号大的点连边 , 至多两条 , 那么我们可以把每个点拆成两个 , 分别连两种边(第一近/第二近) , 

求最近什么的用map好了

然后Dfs过程中把每个元素的深度压入栈里 , 显然栈中元素递增 , 那么我们就可以用lower_bound两个问题一起求了~~

#emacs是最优越的操作系统

 

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <cmath>
#include <vector>
#define travel(x, i) for (int i = fir[x]; i; i = e[i].nxt)
using namespace std;

typedef long long LL;
const int N = 1e5 + 5;
const int INF = 2e9;

struct edge {
  int nxt, to;
} e[N << 1];
int fir[N << 1], cnt = 0;

inline void addedge(int x, int y) {
  e[++ cnt] = (edge){fir[x], y};
  fir[x] = cnt;
}

map <int, int> tab;
int h[N];
int A[N << 1], B[N << 1];
LL sta[N << 1], depa[N << 1], depb[N << 1];
int id[N << 1], top = 0;
bool vis[N << 1];
int n, x0;
double Min_Ratio = 1e15;
int ans0 = 0;
vector <int> que[N];
int X[N], ansa[N], ansb[N];

inline void Upd(int &Min1, int &Min2, int &id1, int &id2, int val, int id) {
  if (Min1 > val) {
    Min2 = Min1; id2 = id1;
    Min1 = val; id1 = id;
  }
  else if (Min2 > val) {
    Min2 = val; id2 = id;
  }
}

inline void dfs(int x, int pa) {
  vis[x] = 1;
  depa[x] = depa[pa] + A[x];
  depb[x] = depb[pa] + B[x];
  id[++ top] = x;
  sta[top] = depa[x] + depb[x];
  if (x <= n) {
    int p = lower_bound(sta + 1, sta + top + 1, sta[top] - x0) - sta;
    p = id[p];
    double t = 1.0 * (depa[x] - depa[p]) / (depb[x] - depb[p]);
    if (t < Min_Ratio || (t == Min_Ratio && h[x] > h[ans0])) Min_Ratio = t, ans0 = x;
    for (vector <int> :: iterator it = que[x].begin(); it != que[x].end(); it ++) {
      p = (*it);
      int l = lower_bound(sta + 1, sta + top + 1, sta[top] - X[p]) - sta;
      l = id[l];
      ansa[p] = depa[x] - depa[l];
      ansb[p] = depb[x] - depb[l];
    }
  }
  travel(x, i) dfs(e[i].to, x);
  top --;
}

int main() {
  scanf("%d", &n);
  for (int i = 1; i <= n; i ++) scanf("%d", &h[i]);
  scanf("%d", &x0);
  map <int, int> :: iterator it;
  int Min1, Min2, id1, id2;
  for (int i = n; i; i --) {
    id1 = id2 = 0;
    Min1 = Min2 = INF;
    tab[h[i]] = i;
    it = tab.find(h[i]);
    if (it != tab.begin()) {
      it --;
      Upd(Min1, Min2, id1, id2, abs(it -> first - h[i]), it -> second);
      if (it != tab.begin()) {
        it --;
        Upd(Min1, Min2, id1, id2, abs(it -> first - h[i]), it -> second);
        it ++;
      }
      it ++;
    }
    it ++;
    if (it != tab.end()) {
      Upd(Min1, Min2, id1, id2, abs(it -> first - h[i]), it -> second);
      it ++;
      if (it != tab.end()) {
        Upd(Min1, Min2, id1, id2, abs(it -> first - h[i]), it -> second);
      }
    }
    if (id2) addedge(id2 + n, i), A[i] = Min2;
    if (id1) addedge(id1, i + n), B[i + n] = Min1;
  }
  int m;
  scanf("%d", &m);
  for (int i = 1, s; i <= m; i ++) {
    scanf("%d%d", &s, &X[i]);
    que[s].push_back(i);
  }
  for (int i = (n << 1); i; i --)
    if (!vis[i]) dfs(i, 0);
  printf("%d\n", ans0);
  for (int i = 1; i <= m; i ++) printf("%d %d\n", ansa[i], ansb[i]);
  return 0;
}