bzoj 4423 [AMPPZ2013]Bytehattan（对偶图，并查集）

Posted 2020-07-02

 

【题目链接】

 

    http://www.lydsy.com/JudgeOnline/problem.php?id=4423

 

【题意】

 

    给定一个平面图，随时删边，并询问删边后两点是否连通。强制在线。

 

【科普】

 

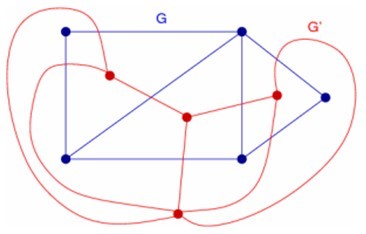
    设有平面图G=(V,E)，满足下列条件的图G‘= (V‘,E‘) 称为图G的对偶图：G的任一面Ri内有且仅有一点Vi‘；对G的域Ri和Rj的共同边界Ek，画一条边Ek‘=(Vi‘,Vj‘)且只与Ek交于一点；若Ek完全处于Ri中，则Vi‘有一自环Ek‘，如下图G‘是G的对偶图：

 

    From here

 

【思路】

 

    如果不强制在线的话，就是BC上的一道题，可以时光倒流+并查集来做。

    加上强制在线，我们将平面图转化为它的对偶图，两点之间删边的操作使得两个平面连通，当对应的两个平面不连通的时候，说明两点之间有环，此时删边后两点依旧连通。并查集维护连通性。

 

【代码】

 

 1 #include<cstdio>
 2 #include<iostream> 
 3 #define FOR(a,b,c) for(int a=b;a<=c;a++)
 4 using namespace std;
 5 
 6 const int N = 1500+10;
 7 
 8 int id[N][N],n,K;
 9 
10 struct UFS {
11     int fa[N*N];
12     UFS() { FOR(i,0,N*N-1) fa[i]=i; }
13     int Find(int u) {
14         return u==fa[u]? u:fa[u]=Find(fa[u]);
15     }
16     void Union(int u,int v) {
17         u=Find(u),v=Find(v);
18         if(u!=v) fa[u]=v; 
19     }
20 } s;
21 
22 int main()
23 {
24     scanf("%d%d",&n,&K);
25     int cnt=0;
26     //id[0][..]||id[..][0] <- 0
27     FOR(i,1,n-1) FOR(j,1,n-1)
28         id[i][j]=++cnt;
29     int b,c,e,f,ans=1;
30     char a[2],d[2];
31     FOR(i,1,K) {
32         if(ans)
33             scanf("%d%d%s%d%d%s",&b,&c,&a,&e,&f,&d);
34         else 
35             scanf("%d%d%s%d%d%s",&e,&f,&d,&b,&c,&a);
36         if(a[0]==‘N‘) e=b-1,f=c;
37         else e=b,f=c-1;
38         if(ans=(s.Find(id[b][c])!=s.Find(id[e][f])))
39             s.Union(id[b][c],id[e][f]);
40         puts(ans?"TAK":"NIE");
41     }
42     return 0;
43 }