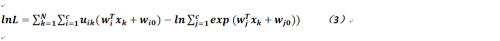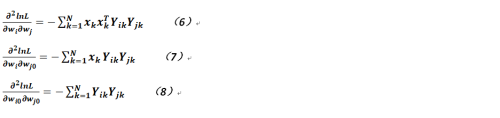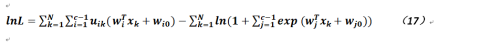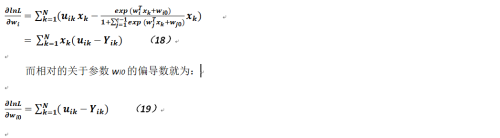关于机器学习中基于对数线性回归模型的讨论

Posted 2020-10-11

前言

  在之前的关于回归问题的讨论中，笔者主要给出了一般原始的线性回归模型（主要以最小二乘法形式进行的）以及其它两种主流的线性回归模型的补充内容，它们主要是为了解决样本之间存在线性相关性的问题，包括岭回归和LASSO回归。

  一般而言，对于多分类问题，我们希望能将样本的采样值约束在一定范围之内，最为常用的如[0,1]之间，这就产生了所谓归一化的需求，就是本文讨论的目标。在下面的章节中，我们着重于此类方法，主要包括经常被使用的Softmax和Logistic回归。

Softmax回归

  按照老规矩，对于N个样本，我们记作，而样本需要被划分为c个类别，如前所述我们需要把样本的取值归一化到[0,1]区间，那么定义每个样本归属某个分类i的概率为：

   上式就是我们熟悉的所谓Softmax表达式。

  需要说明的一点是，为了统一起见，在上式中笔者将偏置也用w.0来表示，而不是以往习惯使用的b，这种表示方法可能在下面的推导中会比较方便。

             那么如果对于所有样本而言，我们肯定希望使这个概率越大越好，故这里又要使用最大似然法来求解，故我们要求取的目标函数就是：

   其中，uik的取值范围仅在{0,1}之中（即分类是硬划分的），而其之和为1，它就是一个样本k属于类别i的归属度矩阵，而且是One-Hot-Vector。

 

             为了便于计算我们对公式2取对数，如下：

   对于上式我们可以使用梯度下降法进行求解，那么关于wi的偏导数为：

   而关于偏置的偏导数则如下式定义：

   对于公式4和公式5而言，它们也没有闭合解（因为是多元函数的非线性方程），只能使用牛顿-拉菲森方法（Newton-Raphson），关于此方法的具体内容，读者可参考相关介绍，但其思想也基本是利用泰勒公式进行展开推导。

            但需要注意的是，原本公式4和5已经是一阶偏导数形式，而牛顿-拉菲森方法还需要对相关目标函数进行求导，故递推公式会涉及到如下几个目标函数的二阶偏导数，为清晰起见现罗列如下：

   在上述二阶偏导的求解中需要注意当对类j的计算时，需要把原公式（即公式4和5）的分子部分作为常数来看待。

   故可以得到在Softmax方法中，参数更新的方法（基于牛顿-拉菲森方法）为：

   但这里有个问题，因为对于样本而言，如果划分为c类，那么其实只要有c-1组参数即可（可以想象对于而分类问题，我们也只要有1个参数向量即可），故结果存在冗余，即可能出现了无穷多解，那么我们只能在其中找一个最简单的，公式变形如下：

         定义复杂度：

Logistic回归

         与Softmax类似，Logistic回归（简称LR）也是一种常用的线性回归模型，而且在很多电商网站的推荐模型中LR算法是最为常见的，而且其公式和推导过程几乎也与前者如出一辙，只不过唯一不同点就是，对于第c类的输出是由其它c-1类来表示的（故这里与Softmax不同，没有那些冗余的解），我们有如下公式，当时，有：

   公式16看上去有点像Sigmoid函数。

         于是对于每一个样本而言我们试图使其乘积的概率最大，故与Softmax类似的我们有（针对公式15）：

   我们可以对上式使用梯度下降法进行求解，那么关于参数wi的偏导数就为：

   可以看出其实上述公式与上面所推导的Softmax相关参数的偏导公式几乎没什么两样，当然其求解方法也就没有什么不同，而我们为了得到wi和wi0的值，也需要计算如下几个二阶偏导数：

   那么对于公式18，我们也需要定义海森矩阵，如下（注意其维度和Softmax的略为不同）：

   而对于海森矩阵中的每个元素而言，其定义则完全和上节中的相应公式一样，为节省篇幅，这里不再列出，其参数更新迭代的方式也完全相同，也不再赘述。