机器学习基石：07 The VC Dimension

Posted 2020-10-09

当N大于等于2，k大于等于3时，

易得：m_H(N)被N^k-1给bound住。

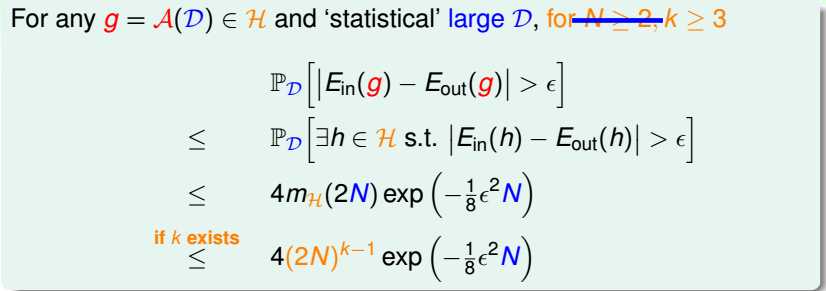
VC维：最小断点值-1/H能shatter的最大k值。

这里的k指的是存在k个输入能被H给shatter，不是任意k个输入都能被H给shatter。

如：2维感知机能shatter平面上呈三角形排列的3个样本点，却shatter不了平面上呈直线排列的3个样本点，

因为当另外2个点标签值一致时，中间那个点无法取与它们相反的标签值。

若无断点，则该H下，VC维为无穷。

所以，存在断点--->有限VC维。

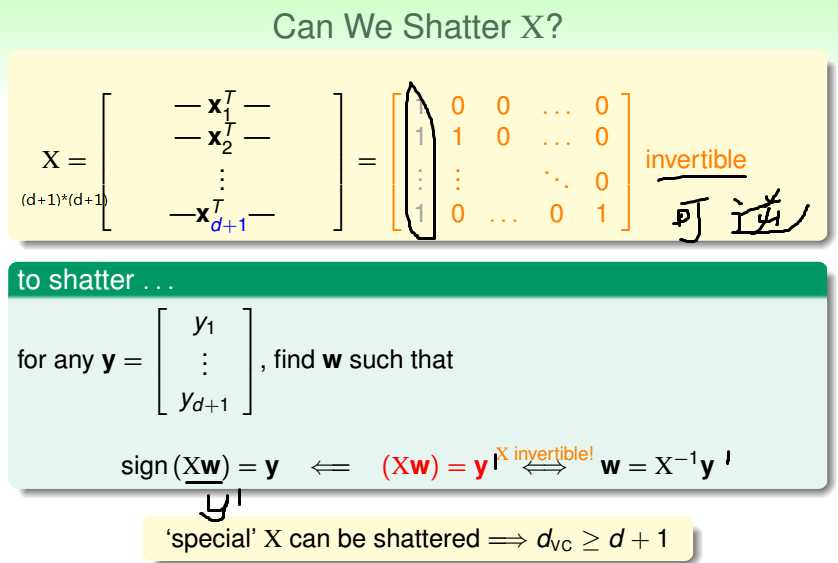
d维感知器算法下，VC维=d+1。

证明：

D，大小为d+1--->矩阵X，易得X是(d+1)*(d+1)的矩阵，X的秩小于等于d+1，

所以存在X，行向量之间线性无关，每一行向量可取任意标签值，

所以H能shatter这个X对应的d+1个样本点，即VC维>=d+1;

D，大小为d+2--->矩阵X，易得X是(d+2)*(d+1)的矩阵，X的秩小于d+2，

所以任意X，总有一行与其他行向量线性相关，该行的标签值收到限制，

所以H不能shatter这个X对应的d+2个样本点，即VC维<=d+1;

所以，VC维=d+1。

VC维，反映的是H的自由度，可粗略认为是自由参数的个数（不总是）。

VC维增大，E_in减小，模型复杂度增大；

VC维减小，E_in增大，模型复杂度减小。

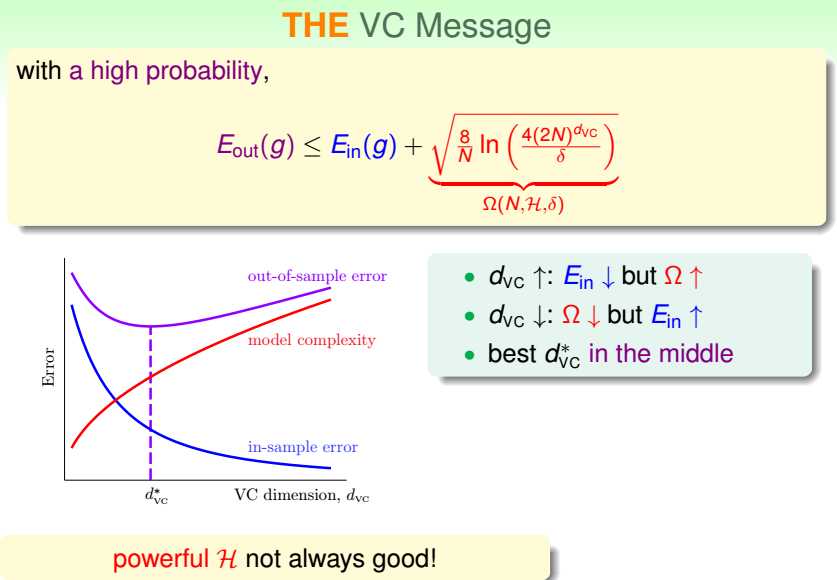
给定差异容忍度epsilon，概率容忍度delta，VC维，求满足条件需要多少样本。

理论上，N约等于10000倍的VC维，

实际上，N取10倍的VC维就足够了。

可见，VC维是十分松弛的，

1.使用霍夫丁不等式，不管f、输入分布P；

2.使用成长函数，不管具体的D；

3.使用N的多项式，不管H(VC维相同)；

4.使用联合bound，不管A。

之所以使用VC维是为了定性分析VC维里包含的信息，

而且它对所有模型都近似松弛。