空间谱专题12：二维测向的基本方法

Posted 2020-10-09 桂。

作者：桂。

时间：2017-10-01  16:50:08

链接：http://www.cnblogs.com/xingshansi/p/7617442.html 

---

前言

圆阵、面阵、L阵、十字阵、V形阵，都是直接地二维求解，复杂度较高，这里梳理复杂度较低的求解算法。

一、二维角度估计的问题

　　以L阵为例，L阵 = 水平线阵 + 垂直线阵，仅仅利用水平测角、垂直测角，然后联立求解二维角度，信息量是不够的。这就好比，利用fx、fy的边界概率，估计出f(x,y)的联合概率密度，通常难以实现。一来不能确定信号个数，二来无法判断信号的入射角度。

clc;clear all;
theta = [ 10 30]/180*pi;
phi = [-20 20]/180*pi;
alpha = sin(theta).*cos(phi);
belta = sin(theta).*sin(phi);
%排列组合各种可能
alpha_all = [alpha,alpha];
belta_all = [belta,fliplr(belta)];

phi_est = atan(belta_all./alpha_all)/pi*180;
alpha_est = asin(alpha_all./cos(phi_est/180*pi))/pi*180;

[alpha_est;phi_est]

　　入射信号为两个，对应角度：theta = [ 10 30]/180*pi;  phi = [-20 20]/180*pi;

实际可能的角度为：

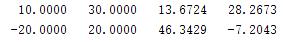
且最少为两个信号，最多为四个信号，对应排列组合： 

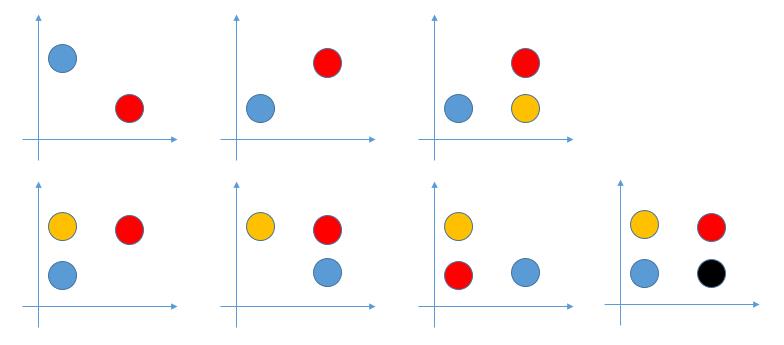
虽然有多种组合，但对于空间谱算法（以MUSIC为例），将各种解反带回MUSIC谱估计，再借助ML算法（即找出最大值），即可实现角度的测量。

如果希望最多解3批相干信号（共4个相干信号），分别按两个一维的布阵：

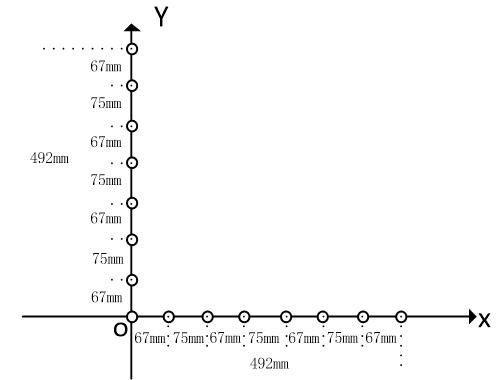
对应两个一维的解算：

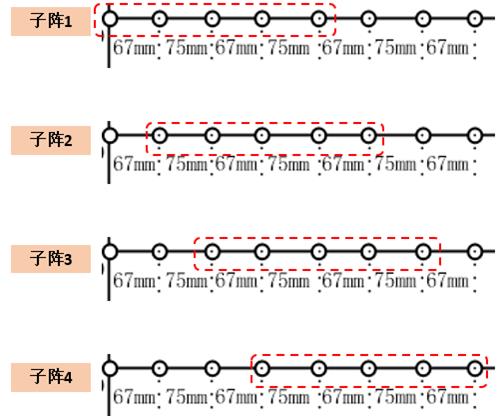
一个基本的特性是：复用阵元越多，则相干信号的盲区出现概率越大，严格来讲，该布阵方案并不可用。