NOIP 2002

Posted 2020-10-09 drizzly

T1：均分纸牌

题目描述

有 N 堆纸牌，编号分别为 1，2，…, N。每堆上有若干张，但纸牌总数必为 N 的倍数。可以在任一堆上取若干张纸牌，然后移动。

移牌规则为：在编号为 1 堆上取的纸牌，只能移到编号为 2 的堆上；在编号为 N 的堆上取的纸牌，只能移到编号为 N-1 的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。

现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。

例如 N=4，4 堆纸牌数分别为：

①9②8③17④6

移动3次可达到目的：

从 ③ 取 4 张牌放到 ④ （9 8 13 10） -> 从 ③ 取 3 张牌放到 ②（9 11 10 10）-> 从 ② 取 1 张牌放到①（10 10 10 10）。

输入输出格式

输入格式：

 

键盘输入文件名。文件格式：

N（N 堆纸牌，1 <= N <= 100）

A1 A2 … An （N 堆纸牌，每堆纸牌初始数，l<= Ai <=10000）

 

输出格式：

 

输出至屏幕。格式为：

所有堆均达到相等时的最少移动次数。

 

输入输出样例

输入样例#1：

4
9 8 17 6

输出样例#1：

3

Solution：

　　本题只需要模拟一下。

　　首先预处理求出平均值，如果为0则不需要移动。然后固定从1或N开始移动牌堆，for一下就好了~

　　//可能出现负数

 1 #include<cstdio>
 2 using namespace std;
 3 int n,a[105],sum=0,cnt=0,p=0;
 4 int main(){
 5     scanf("%d",&n);
 6     for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum+=a[i];
 7     p=sum/n;
 8     for(int i=1;i<=n;i++) a[i]-=p;
 9     for(int i=1;i<=n;i++) {
10         if(!a[i]) continue;
11         a[i+1]+=a[i];
12         cnt++;
13     } 
14     printf("%d",cnt);
15     return 0;
16 }

 

T3 自由落体

题目描述

在高为 H 的天花板上有 n 个小球，体积不计，位置分别为 0，1，2，…．n-1。在地面上有一个小车（长为 L，高为 K，距原点距离为 S1）。已知小球下落距离计算公式为 d＝1/2*g*(t^2)，其中 g=10，t 为下落时间。地面上的小车以速度 V 前进。

如下图：

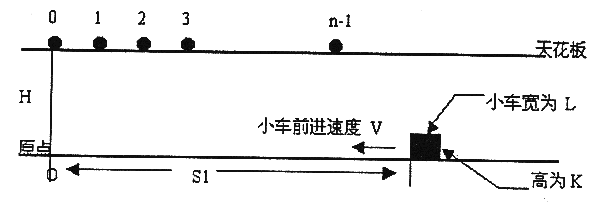
小车与所有小球同时开始运动，当小球距小车的距离 <= 0.0001(感谢Silver_N修正) 时，即认为小球被小车接受（小球落到地面后不能被接受）。

请你计算出小车能接受到多少个小球。

输入输出格式

输入格式：

 

键盘输人：

H，S1，V，L，K，n （l<=H，S1，V，L，K，n <=100000）

 

输出格式：

 

屏幕输出：

小车能接受到的小球个数。

 

输入输出样例

输入样例#1：

5.0 9.0 5.0 2.5 1.8 5

输出样例#1

   1

Solution：

　　这是一个有精度的题目。

　　也是简单模拟，分别求出两个零界点，然后进行判断。

　　嗯，代码有点短...

 1 #include<cstdio>
 2 #include<cmath>
 3 using namespace std;
 4 int n,ans=0;
 5 double h,s,v,l,k;
 6 int main(){
 7     scanf("%lf%lf%lf%lf%lf%d",&h,&s,&v,&l,&k,&n);
 8     double ll,rr;
 9     ll=-0.0001+(s-sqrt(h/5)*v);
10     rr= 0.0001+(s-sqrt((h-k)/5)*v)+l;
11     for(int i=0;i<n;i++) if(i<rr&&i>ll) ans++;
12     printf("%d",ans);
13     return 0;
14 }