1624 取余最长路 (前缀和+set二分)

Posted 2020-10-08 心之所向 素履以往

 

1624 取余最长路

佳佳有一个n*m的带权矩阵，她想从(1,1)出发走到(n,m)且只能往右往下移动，她能得到的娱乐值为所经过的位置的权的总和。

有一天，她被下了恶毒的诅咒，这个诅咒的作用是将她的娱乐值变为对p取模后的值，这让佳佳十分的不开心，因为她无法找到一条能使她得到最大娱乐值的路径了！

她发现这个问题实在是太困难了，既然这样，那就只在3*n的矩阵内进行游戏吧！

现在的问题是，在一个3*n的带权矩阵中，从(1,1)走到(3,n)，只能往右往下移动，问在模p意义下的移动过程中的权总和最大是多少。

样例解释：

移动的方案为“下下右”。

Input

单组测试数据
第一行两个数n(1<=n<=100000),p(1<=p<=1000000000)。
接下来3行，每行n个数，第i行第j列表示a[i][j]表示该点的权(0<=a[i][j]<p)。

Output

一个整数表示答案。

Input示例

2 3
2 2
2 2
0 1

Output示例

2


由于矩阵只有三行 我们画一个图 

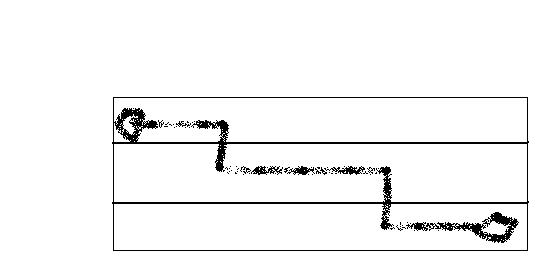
很容易看出来 整条路径分成三行 只有两个拐点 

路径中是有三条线段的 我们可以统计每一行的前缀和 

所以我们有下面的计算公式 sum[1][x]+sum[2][y]-sum[2][x-1]+sum[3][n]-sum[3][y-1] 
把上述式子换一下位置 sum[1][x]+sum[2][x-1]   +   sum[2][y]+sum[3][n]-sum[3][y-1]

所以 我们可以想到来枚举 x 和 y 寻找最长路径 从图中可以看出 两个拐点的关系 x<=y 这个很重要 
数据n<=10^5 所以 n^2 枚举会超时 
或许我们可以从两个拐点的关系上下手 
因为x<=y 所以我们可以O(n) 枚举x 把sum[1][x]+sum[2][x-1] 放入一个集合 

二分查找 大于等于sum[2][y]+sum[3][n]-sum[3][y-1]的值 
这样就把复杂度降到 O(nlongn) 

 1 #include <set>
 2 #include <cstdio>
 3 #include <cctype>
 4 
 5 const int MAXN=100010;
 6 
 7 typedef long long LL;
 8 
 9 int n,p;
10 
11 LL ans;
12 
13 LL sum[4][MAXN];
14 
15 inline void read(LL&x) {
16     int f=1;register char c=getchar();
17     for(x=0;!isdigit(c);c==\'-\'&&(f=-1),c=getchar());
18     for(;isdigit(c);x=x*10+c-48,c=getchar());
19     x=x*f;
20 }
21 
22 int hh() {
23     scanf("%d%d",&n,&p);
24     for(int i=1;i<=3;++i)
25       for(int j=1;j<=n;++j)
26         read(sum[i][j]),sum[i][j]=(sum[i][j]+sum[i][j-1])%p;
27     std::set<LL> s;
28     std::set<LL>::iterator it;
29     for(int i=1;i<=n;++i) { // 在一个循环中 保证了x<=y 
30                                             // 不在一个循环中 可能会出现 向左走的情况  即 x>y 这是不合法的 
31          LL t=(sum[1][i]-sum[2][i-1]+p)%p;
32         s.insert(t);
33         t=(sum[2][i]-sum[3][i-1]+sum[3][n]+p)%p;
34         it=s.lower_bound(p-t);
35         if(it!=s.begin()) ans=ans>(t+*(--it))%p?ans:(t+*it)%p;
36     }
37     printf("%lld\\n",ans);
38     return 0;
39 }
40 
41 int sb=hh();
42 int main(int argc,char**argv) {;}

代码