软件工程第一次作业——数独的求解与生成

Posted 2020-10-08 LiuSD

代码的GitHub地址：https://github.com/Liu-SD/sudoku

personal software process stages	预估耗时	实际耗时
计划
估计这个任务需要多少时间	10 min	10 min
开发
需求分析（包括学习新技术）	180 min	190 min
生成设计文档	0 min(没做设计文档)	0 min
设计复审（和同事审核设计文档）	0 min(没有同事复审)	0 min
代码规范（为目前的开发制定合适的规范）	30 min	60 min
具体设计	180 min	180 min
具体编码	240 min	240 min
代码复审	60 min	180 min
测试（自我测试，修改代码，提交修改）	60 min	50 min
报告
测试报告	180 min	180 min
计算工作量	0 min(没有做这项工作)	0 min
事后总结，并提出过程改进计划	30 min	30 min
合计	1070 min	1160 min

 

解题思路描述

题目要求分为两个部分，一个是解数独，一个是自动生成数独。并且生成数独时对第一个数字做出了限制。所以可以认为自动生成数独是只有一个数字限制时的解数独。所以说这两者大部分的实现算法是相同的。解数独时是在找到第一个解的时候返回真，而生成数独是在找到第N个解时返回真。

因此问题转换为在R个限制条件（1<=R<=81）的情况下寻找到N(1<=N<=1000000)个解时返回真，否则返回假。解的输出可以把输出流作为参数传入，找到一个答案时将答案输出。这个问题是典型的回溯问题，在网上查资料了解到可以将问题转化为精确覆盖问题，使用DLX（dancing link）算法实现。DLX的重点在于十字链表的实现。

设计实现过程

实现算法的第一步需要使用十字链表表示稀疏矩阵。我把十字链表封装为cross_link类，这个类，类中包括build方法，建立空的矩阵。build函数在构造函数中调用。稀疏矩阵建立以后，head指向矩阵头，rows数组存放行的头指针，cols数组存放列的头指针。类中包括insert方法插入元素。delrow，delcol，recoverrow，recovercol四个方法删除或恢复整行或整列。这四个方法将是算法实现的关键。在删除行（列）时，修改每一行（列）中元素的邻居节点到另一侧，同时保留被删除行（列）的邻居指针，方便恢复。删除和恢复需要以栈的方式操作。即后删除的先恢复。

算法被封装到dlx类中，dlx类调用并维护cross_link类的实例。类中的find_one和find_many实现解数独和生成数独两个需求。find_one调用_find_one递归函数，find_many调用_find_many递归函数。

_find_one函数流程：

1. 如果head的右结点为空，即矩阵没有列，则将result数组结果输出，stack中的所有删除操作使用recover做逆操作，即恢复为最初始的矩阵。返回真。

2. 否则，找到元素最少的列min_col_index，对于这一列的每一个元素i：

　　将元素i所在行压如result栈中。

　　对于元素i所在行的每个元素j：

　　　　对于元素j所在列的每个元素p：

　　　　　　删除p所在的行，压如stack栈中。

　　　　删除j所在的列，压如stack栈中。

　　以stack和result栈的栈顶指针为参数递归调用自己，如果为真，返回真。

　　否则，把元素i从result栈弹出。

　　把这一次压如stack栈中的元素弹出并且recover函数恢复删除的行和列。

函数最后返回假。

_find_many函数和_find_one类似，在找到结果时将结果输出到文件，计数器加一，在计数器等于目标数目之前都一直返回假。

十字链表的搭建容易出错，而且增删操作对于之后的算法十分重要，因此单元测试的重点放在了十字链表类的测试。设计单元测试时，先测试十字链表的插入操作，每插入一个元素，就计算元素个数并且断言。之后测试链表的删除行（列）以及之后行（列）的复原。

程序性能改进

我在程序性能改进方面没有做很多的操作，仅仅将输出到文件的部分从逐个数字写入改为了一个数独盘的一次性写入。但这个改进大大提升了程序的性能。生成一百万个数独从之前的五分钟变为当前的十四秒。

于是，进一步的，我修改了从文件读入的方式，将之前的逐个数字读入改为逐行读入。

生成一百万个数独时，VS性能分析图：

执行次数最多的函数为：

 

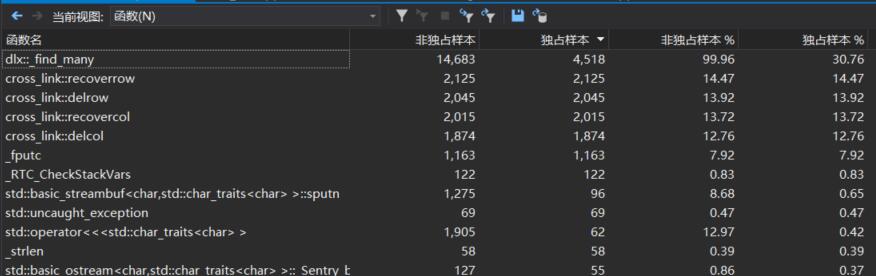
由此可见递归调用_find_many的执行次数最多，对链表的四个操作十分频繁，对其进行优化十分重要。

上图是递归调用的函数关系图。

代码说明

十字链表类的关键代码为删除和恢复行或者列。

 

void cross_link::delrow(int r) {
    for (Cross i = rows[r]; i != NULL; i = i->right) { // 对于该行每一个元素
        cols[i->col]->count--; // 删除后该列的计数器减一
        if (i->up)
            i->up->down = i->down; // 在它上方存在元素的情况下，上方元素改为指向该元素下方元素
        if (i->down)
            i->down->up = i->up; // 下方元素同理
    }
}

void cross_link::recoverrow(int r) {
    for (Cross i = rows[r]; i != NULL; i = i->right) { // 对于该行每一个元素
        cols[i->col]->count++; // 恢复后该列的计数器加一
        if (i->up)
            i->up->down = i; // 在上方元素不空的情况下，将原本指向自己下方的上方元素指回自己
        if (i->down)
            i->down->up = i; // 下方元素同理
    }
}

 

 

 

以上是行的删除和恢复一行元素的代码，删除恢复列的情形和一上代码类似。

dlx类的关键代码为函数的递归调用。以下是_find_many的代码：

 

 1 bool dlx::_find_many(int stack_top, int result_pos, int N, int & n, std::ofstream &fout)
 2 {
 3     if (!head->right) { // 在链表不存在列的情况下，
 4         int matrix[9][9];
 5         for (int i = 0; i < 81; i++) { // 将result数组里面的解翻译为9*9的矩阵
 6             int j = result[i] - 1;
 7             int val = j % 9 + 1;
 8             int pos = j / 9;
 9             int row = pos / 9;
10             int col = pos % 9;
11             matrix[row][col] = val;
12         }
13         char str[19 * 9 + 2] = { 0 };
14         for (int i = 0; i < 9; i++) { // 用字符串记录矩阵并输出到文件
15             for (int j = 0; j < 9; j++) {
16                 str[i * 19 + 2 * j] = matrix[i][j] + \'0\';
17                 str[i * 19 + 2 * j + 1] = \' \';
18             }
19             str[i * 19 + 18] = \'\\n\';
20         }
21         str[19 * 9] = \'\\n\';
22         str[19 * 9 + 1] = \'\\0\';
23         fout << str;
24         if (++n >= N) // 计数器加一，如果大于要求的数量，返回真，否则返回假
25             return true;
26         else
27             return false;
28     }
29     int min_col_count = 100;
30     int min_col_index = -1;
31     for (Cross p = head->right; p != NULL; p = p->right) { // 找到元素最少的列
32         if (min_col_count > p->count) {
33             min_col_count = p->count;
34             min_col_index = p->col;
35         }
36     }
37     for (Cross a = cols[min_col_index]->down; a != NULL; a = a->down) { // 对于该列的所有元素
38         result[result_pos++] = a->row; // 将该元素的行号压如result栈中
39         int new_stack_top = stack_top;
40         for (Cross b = rows[a->row]->right; b != NULL; b = b->right) { // 对于该元素所在行的所有元素
41             for (Cross c = cols[b->col]->down; c != NULL; c = c->down) { // 对于该元素所在列的所有元素
42                 A->delrow(c->row); // 删除该元素所在行
43                 stack[new_stack_top++] = c->row; // 并记录下删除操作（删除行时压入正的行号，删除列时压入负的列号）
44             }
45             A->delcol(b->col); // 删除该元素所在列
46             stack[new_stack_top++] = -b->col; // 记录删除操作
47         }
48         if (_find_many(new_stack_top, result_pos, N, n, fout)) // 调用下一级函数，如果找到的数独数量达到了需求，则返回真
49             return true;
50         for (int i = new_stack_top - 1; i >= stack_top; i--) { // 否则将压入stack栈中的删除操作弹出，并且做其逆操作
51             if (stack[i] > 0)
52                 A->recoverrow(stack[i]);
53             else
54                 A->recovercol(-stack[i]);
55         }
56         result_pos--; // 最后将部分解从result数组中弹出，进入下一轮循环
57     }
58     return false;在循环完所有情况还没有达到数量需求的情况下，返回假
59 }

 

 

 

以下是_find_one的代码：

 

 1 bool dlx::_find_one(int stack_top, int result_pos)
 2 {
 3     if (!head->right) { // 找到一个解时记录答案并且直接返回真
 4         for (int i = stack_top - 1; i >= 0; i--) {
 5             if (stack[i] > 0)
 6                 A->recoverrow(stack[i]);
 7             else
 8                 A->recovercol(-stack[i]);
 9         }
10         return true;
11     }
12     int min_col_count = 100;
13     int min_col_index = -1;
14     for (Cross p = head->right; p != NULL; p = p->right) {
15         if (min_col_count > p->count) {
16             min_col_count = p->count;
17             min_col_index = p->col;
18         }
19     }
26     for (Cross a = cols[min_col_index]->down; a != NULL; a = a->down) {
27         result[result_pos++] = a->row;
28         int new_stack_top = stack_top;
29         for (Cross b = rows[a->row]->right; b != NULL; b = b->right) {
30             for (Cross c = cols[b->col]->down; c != NULL; c = c->down) {
31                 A->delrow(c->row);
32                 stack[new_stack_top++] = c->row;
33             }
34             A->delcol(b->col);
35             stack[new_stack_top++] = -b->col;
36         }
37         if (_find_one(new_stack_top, result_pos))
38             return true;
39         for (int i = new_stack_top - 1; i >= stack_top; i--) {
40             if (stack[i] > 0)
41                 A->recoverrow(stack[i]);
42             else
43                 A->recovercol(-stack[i]);
44         }
45         result_pos--;
46     }
47     return false;
48 }

 

 

 

 

程序实现完成。_find_one和_find_many存在代码冗余的现象，下一步修改目标是将冗余部分抽取出来或是将两个函数合并为一个。