9.23——清北模拟赛

Posted 2020-10-08

T 1 ． 回形遍历( ( calc .cpp/c/pas)

时间限制：1 1s s
内存 限制： 256MB
【问题 描 述】
给出一个 n*m 的棋盘，按如下方式遍历，请问(x,y)往后 z 步走到的是哪个格子。

 

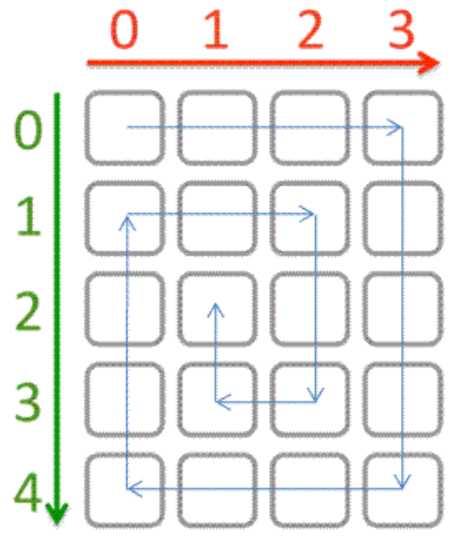
【输入】
输入文件名为 calc.in。
一行，包含五个整数：n,m,x,y,z
【输出】
输出文件名为 calc.out。
输出一行，包含两个整数，表示所在格子的横纵坐标
【输入输出样例】
calc .in        calc .out
4 5 3 0 5     2 4
【 样例解释 】

 

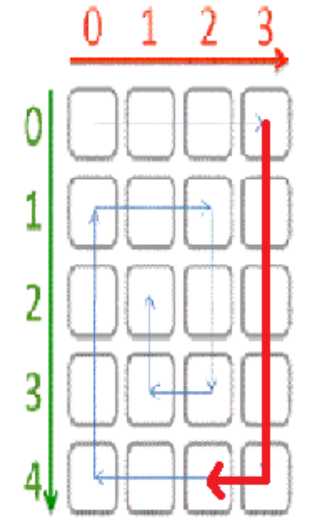
【数据说明】
对于 70%的数据，1<=n,m,z<=1000,0<=x<n,0<=y<m
对于 100%的数据，1<=n,m,z<=100000,0<=x<n,0<=y<m

 

 1 #include <cstdio>
 2 
 3 #define min(a,b) (a<b?a:b)
 4 inline void read(int &x)
 5 {
 6     x=0; register char ch=getchar();
 7     for(; ch>‘9‘||ch<‘0‘; ) ch=getchar();
 8     for(; ch>=‘0‘&&ch<=‘9‘; ch=getchar()) x=x*10+ch-‘0‘;
 9 }
10 const int N(1000+5);
11 int m,n,y,x,z,tot,cnt[N][N];
12 struct Pos {
13     int x,y;
14     Pos() { x=0, y=0; }
15 }pos[N*N];
16 
17 int Presist()
18 {
19     freopen("calc.txt","r",stdin);
20     freopen("calc.out","w",stdout);
21     read(m),read(n);
22     tot=cnt[x=0][y=0]=1;
23     int total=n*m;
24     for(; tot<total; )
25     {
26         for(; tot<total&&!cnt[x][y+1]&&y+1<m; )
27         {
28             cnt[x][++y]=++tot;
29             pos[tot].x=x;
30             pos[tot].y=y;
31         }
32         for(; tot<total&&!cnt[x+1][y]&&x+1<n; )
33         {
34             cnt[++x][y]=++tot;
35             pos[tot].x=x;
36             pos[tot].y=y;
37         }
38         for(; tot<total&&!cnt[x][y-1]&&y-1>=0; )
39         {
40             cnt[x][--y]=++tot;
41             pos[tot].x=x;
42             pos[tot].y=y;
43         }
44         for(; tot<total&&!cnt[x-1][y]&&x-1>=0; )
45         {
46             cnt[--x][y]=++tot;
47             pos[tot].x=x;
48             pos[tot].y=y;
49         }
50     }
51     read(y),read(x),read(z); z+=cnt[x][y];
52     printf("%d %d\\n",pos[z].y,pos[z].x);
53     return 0;
54 }
55 
56 int Aptal=Presist();
57 int main(int argc,char*argv[]){;}

绕着圈一直转，70分暴力

 

 

T2 2 ． 排列( ( sum .cpp/c/pas)

时间限制：1 1s s
内存 限制： 256MB
【问题 描 述】
给出一个随机的排列， 请你计算最大值减最小值的差小于等于 0~n-1 的区间分别有多少
个。
【输入】
TYVJ.CN
输入文件名为 sum.in。
第一行一个数 T(<=10)，表示数据组数
对于每一组数据：
第一行一个数 n（1<=n<=100,000）
第二行 n 个数 a1...an，表示一个随机的排列
【输出】
输出文件名为 sum.out。
对于每组数据输出 n 行，分别表示差值小于等于 0~n-1 的区间个数
【输入输出样例】
sum .in sum .out
1
4
3 2 4 1
4
5
7
10
【数据说明】
对于 30%的数据，1<=n<=300；
对于 60%的数据，1<=n<=5000
对于 100%的数据，1<=n<=100000

 1 #include <cstring>
 2 #include <cstdio>
 3 
 4 #define max(a,b) (a>b?a:b)
 5 #define min(a,b) (a<b?a:b)
 6 inline void read(int &x)
 7 {
 8     x=0; register char ch=getchar();
 9     for(; ch>‘9‘||ch<‘0‘; ) ch=getchar();
10     for(; ch>=‘0‘&&ch<=‘9‘; ch=getchar()) x=x*10+ch-‘0‘;
11 }
12 const int N(100005);
13 int n,num[N],ans[10000005];
14 
15 int Presist()
16 {
17     freopen("sum.in","r",stdin);
18     freopen("sum.out","w",stdout);
19     int t; read(t);
20     for(int max_,min_; t--; )
21     {
22         read(n); memset(ans,0,sizeof(ans));
23         for(int i=1; i<=n; ++i) read(num[i]);
24         for(int l=1; l<=n; ++l)
25         {
26             max_=min_=num[l];
27             for(int r=l; r<=n; ++r)
28             {
29                 max_=max(max_,num[r]);
30                 min_=min(min_,num[r]);
31                 ans[max_-min_]++; 
32             }
33         }
34         for(int i=0; i<n; ++i)
35             printf("%d\\n",ans[i]),ans[i+1]+=ans[i];
36     }
37     return 0;
38 }
39 
40 int Aptal=Presist();
41 int main(int argc,char*argv[]){;}

60分暴力：n^2枚举，枚举左端点，向右更新区间最值。

 

 

3. 近似 排列计数（ count .cpp/c/pas)

时间限制：1 1s s
内存 限制： 256MB
【问题 描 述】
对于一个 1～n 的排列，如果满足第 i 个数|a i -i|<=k，则称该排列为 K-近似排列。
现在排列的若干位置已经确定， 你需要计算剩下的数有多少种排列方法使得形成的排列
是 K-近似排列。
【输入】
输入文件名为 count.in。
第一行一个数 T(<=10)，表示数据组数
对于每一组数据：
第一行三个数 n，m，k，分别表示排列长度、已确定位置的个数和近似参数 K
接下来 m 行，每行两个数 x、y，表示已经确定第 x 个数是 y
【输出】
TYVJ.CN
输出文件名为 count.out。
对于每组数据输出一行，包含一个数，表示方法个数（对 1,000,000,007 取模）
【输入输出样例】
count .in count .out
1
4 1 1
2 3
2
【数据说明】
对于 30%的数据，1<=n，m<=10,k<=2
对于 50%的数据，1<=n,m<=20,k<=2
对于 70%的数据，1<=n<=100000,m<=100,k<=2
对于 100%的数据，1<=n<=10^9,m<=100,k<=2

 

 1 #include <algorithm>
 2 #include <cstdlib>
 3 #include <cstring>
 4 #include <cstdio>
 5 
 6 const int mod(1000000007);
 7 inline void read(int &x)
 8 {
 9     x=0; register char ch=getchar();
10     for(; ch>‘9‘||ch<‘0‘; ) ch=getchar();
11     for(; ch>=‘0‘&&ch<=‘9‘; ch=getchar()) x=x*10+ch-‘0‘;
12 }
13 const int N(100005);
14 int n,m,k,num[N],ans,jc,cnt;
15 int x[111],y[111],must[111];
16 
17 inline bool judge()
18 {
19     for(int i=1; i<=n; ++i)
20         if(abs(num[i]-i)>k) return 0;
21     return true;
22 }
23 
24 int Presist()
25 {
26     freopen("count.in","r",stdin);
27     freopen("count.out","w",stdout);
28     int t; read(t);
29     for(; t--; ans=0)
30     {
31          read(n),read(m),read(k);jc=1;
32          for(int i=1; i<=n; ++i) jc*=i;
33          for(int i=1; i<=m; ++i)
34          {
35              read(x[i]),read(y[i]),must[x[i]]=y[i];
36              if(abs(x[i]-y[i])>k) goto Love;
37          }
38          for(int i=1; i<=n; ++i) num[i]=i;
39          do {
40              for(int i=1; i<=m; ++i)
41                  if(num[x[i]]!=must[x[i]]) goto Pos;
42              if(judge()) ans++,ans%=mod; Pos:;
43          }while(std::next_permutation(num+1,num+n+1));
44 Love     :printf("%d\\n",ans); 
45     }
46     return 0;
47 }
48 
49 int Aptal=Presist();
50 int main(int argc,char*argv[]){;}

爆零暴力、、全排列挨着判