HDU 1820 / uva 861 Little Bishops

Posted 2020-10-05 BK_201

题目：http://acm.hdu.edu.cn/showproblem.php?pid=1820

题意：给你一个n*n的棋盘，让你放k个象，求方法数

 

象的攻击路线是斜的，所以我们可以将棋盘旋转45°，这样攻击路线就成了水平，象就变成了车

之后可以发现，如果将棋盘分为黑白格子，黑白棋子之间是无法互相攻击的，那我们就可以将他们分开考虑

把棋盘处理成2个下面的图形

 

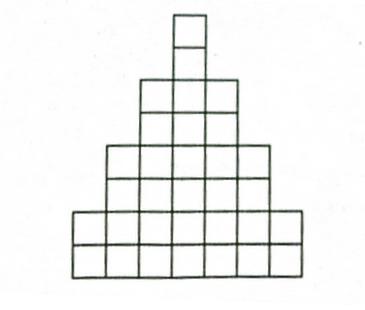
设dp[i][j]表示前i行放了j个车的方法数，c[i]表示第i行可以放置的棋子数量，那么转移方程为：

dp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (c[i] - (j - 1))

需要注意的是c数组应该是增序的，这样才能保证前面的j-1行放了车，对应这一行就有j-1个位

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<map>
#include<set>
using namespace std;
const int N=70;
int n,k;
int c1[N],c2[N],dp1[10][N],dp2[10][N];
void init()//将棋盘分为黑白色，再将棋盘旋转45°
{
    memset(c1,0,sizeof(c1));
    memset(c2,0,sizeof(c2));
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if ((i+j)&1)
                c2[(i+j)>>1]++;//第（i+j）/2斜行有几个格子
            else c1[(i+j)>>1]++;
}
void solve(int dp[N][N],int c[N])
{
    for(int i=0;i<=n;i++)
        dp[i][0]=1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=c[i];j++)
            dp[i][j]=dp[i-1][j]+dp[i-1][j-1]*(c[i]-j+1);
}
int main()
{
    while(scanf("%d%d",&n,&k)&&n+k)
    {
        init();
        sort(c1+1,c1+1+n);
        sort(c2+1,c2+n);
        memset(dp1,0,sizeof(dp1));
        memset(dp2,0,sizeof(dp2));
        solve(dp1,c1);
        solve(dp2,c2);
        int ans=0;
        for(int i=0;i<=k;i++)
            ans+=dp1[n][i]*dp2[n-1][k-i];
        printf("%d\\n",ans);
    }
    return 0;
}