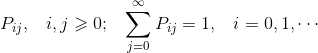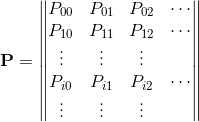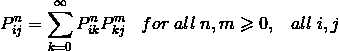Chapter 4 马尔科夫链

Posted 2020-10-04

4.1 引言

现在要研究的是这样一种过程：

表示在时刻的值（或者状态），想对一串连续时刻的值，比如：，， ... 建立一个概率模型。

最简单的模型就是：假设都是独立的随机变量，但是通常这种假设都是没什么根据的，也缺乏研究的意义。

举例来说的话，如果用来代替某个公司，比如Google，在个交易日之后的股票价格。

那么说第天的股票价格和之前第天，第天，第乃至第天的股票价格一点关系都没有，这样是说不过去的。

但是说第天股票的收盘价格依赖于第天的收盘价格还是有点道理的。

同样还可以做出这样的合理假设：在给定了所有过去的收盘价，，...，，那么第天的收盘价格仅仅依赖于第天的收盘价格。这种假设就定义了一个中随机过程，即Markov Chain（马尔科夫链）。

下面给出马尔科夫链的正式定义：

    令是一个取有限或者可数个可能值的随机过程。

    除非明确提到过，这个过程可能的取值将会用非负整数来表示。

    如果，那么该过程就是在时刻的状态为。

    这里假设只要过程是处于状态，那么下一步过程状态转为的概率是固定的。

                               （4.1）

    对所有的状态，，...，和，，和所有的都成立。

上面定义的过程就被称之为马尔科夫链。

方程（4.1）可以解释为：对于马尔科夫链，在给定了过去时刻的状态，，...，和当前的状态，任何未来状态和过去的状态无关，只和当前的状态有关。

代表了过程从状态通过下一步转变到状态的概率。由于概率都是非负的，而且过程随着时间也必须流转到接下来的某个状态，所以可以得到：

令表示一步转移概率的矩阵，那么可以得到

例4.1 天气预报

假设明天是否下雨的依赖于过去的天气条件，但仅限于今天是否下雨，而和之前的天气状态无关。

假设今天下雨，明天也下雨的概率是；今天不下雨，明天下雨的概率是。

令下雨时，过程的状态为，不下雨的时过程的状态为。

那么上述过程就是一个两状态的马尔科夫链，其转移概率矩阵为：

4.2 Chapman-Kolmogorov等式

之前我们已经定义了一步转移概率，现在来定义转移概率，即处于状态的过程经过了步状态改变之后处于状态的概率。

用公式来阐述就是：

显而易见的是。

Chapman-Kolmogorov等式提供了计算步转移概率的方法。

                              （4.2）

对于比较通俗的解释就是过程从状态开始经过了步转移之后到达状态，然后从状态经过步转移之后到达了状态。把中间状态的所有可能的概率加起来就是过程从状态经过了步之后转移到状态的概率了。