马尔科夫链

Posted 2021-02-21 frodo-x

11. 马尔科夫链

(X_0,X_1,...,X_n)，(n)表示时间，如果(X_0, ...X_n)都是独立的，那么这个假设限制性太大，不能对现实世界建模。而如果(X_0, ...X_n)彼此可以任意交互影响，那么模型太难计算。马尔科夫链是单步影响（one-step dependence）的序列，一个折中的假设。

11.1 马尔科夫性质和转移矩阵

马尔科夫链存在时间和空间中，(X_n)的可能取值是状态空间，(n) 是转移过程的时间。时空都是可离散、可连续。现只讨论离散空间、离散时间、有限状态空间的情形。

定义11.1.1：对于取值空间是({1,2,...,M})的随机变量序列(X_0,X_1,...,X_n)，如果对于所有(n>0)，存在

[P(X_{n+1}=j|X_n=i,X_{n-1}=i_{n-1},...,X_0=i_0)=P(X_{n+1}=j|X_n=i) ]

，那么这个序列就是马尔科夫链。(P(X_{n+1}=j|X_n=i))被称为转移概率。本讨论中如果没有明确说明，默认马尔科夫链是时间同性的（time-homogeneous ）,即对于所有时间(n)，转移概率都是相同的。

以上等式即是马尔科夫性质，即只有(X_{n-1})影响到(X_n)。如果(n)代表现在，(n)之前代表过去，(n)之后代表未来，那么马尔科夫性质表示过去和未来是条件独立的。

为了描述马尔科夫链的过程，我们必须知道转移概率(P(X_{n+1}=j|X_n=i))，转移概率编码在转移矩阵里。

定义11.1.2：(X_0,X_1,...,X_n)是取值空间为({1,2,...,M})的马尔科夫链，(q_{ij}=P(X_{n+1}=j|X_n=i))是从(i)到(j)的转移概率，那么(M imes M)矩阵(Q=(q_{ij}))是其转移矩阵。

注意，(Q)是非负矩阵，且每行的和为1。

例11.1.3：（晴天雨天）假设对于任一天，天气只能是晴天或雨天（rainy or sunny ）。如果今天雨，那么明天雨概率(1/3)，明天晴概率(2/3)。如果今天晴，明天雨概率(1/2)，明天晴概率(1/2)。(X_n)表示(n)天的天气，那么(X_0,X_1,...,X_n)时空间状态为({R,S})的马尔科夫链。那么其转移矩阵是：

[left( egin{matrix} 1/3 & 2/3 1/2 & 1/2 end{matrix} ight) ]

也可以用转移状态图表示。

如果明天天气取决于昨天和今天的天气，比如，如果连续两天晴天，下一天必然是雨天，如果连续两天雨天，下一天必是晴天。那么为了符合马尔科夫性质，状态空间变为({(R,R),(R,S),(S,R),(S,S)})，相应的状态转移矩阵也会变化。

定义11.1.4：(n)步转移概率。从(i)经过(n)步后变为(j)的概率，用(q_{ij}^{(n)})表示：

[q_{ij}^{(n)}=P(X_n=j|X_0=i) ]

注意

[q_{ij}^{(2)} = sum_k{q_{ik}q_{kj}} ]

等式右边是(Q^2)矩阵的第((i,j))项，所以(Q^2)给出了(2)步的转移矩阵。归纳可知，(q_{ij}^{(n)}是Q^n的第(i,j)项)。

计算(X_0,X_1,...,X_n)的边缘分布需要转移矩阵和初始状态。初始状态(X_0)可以指定，也可以根据分布随机选取，假设((t_1, t_2,...t_M))是(X_0)的(PMF)，即(t_i=P(X_0=i))，那么边缘分布可以如下计算。

定理11.1.6：(X_n)的边缘分布。令( extbf{t}=(t_1,t_2,...,t_M))，其中(t_i=P(X_0=i))，( extbf{t})是行向量，(X_n)的边缘分布是( extbf{t}Q^n)，即( extbf{t}Q^n)的第(j)项是(P(X_n=j))。

证明：

[P(X_n=j)=sum_{i=1}^{M}{P(X_0=i)P(X_n=j|X_0=i)}=sum_{i=1}^{M}{t_i q_{ij}^{(n)}} ]

11.2 状态的分类

马尔科夫链的状态可以根据其在长期的过程中经常出现或者不出现，分为周期性的（recurrent）和瞬时的（transient）。状态也可以用周期（period）分类，即两次在同一个状态之间的时间。

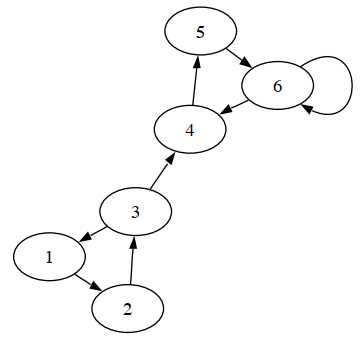
如上图，1、2、3是瞬时的（transient）状态，4、5、6是周期性（recurrent）状态。

定义11.2.1：从状态(i)出发，最终回到状态(i)的概率是1，那么状态(i)就是周期性状态，否则，就是暂时性状态，即说从状态(i)出发后无法回到状态(i)的概率是正值。或者说，只要永远离开状态(i)的概率是正值，那么一定会永远离开状态(i)，离开状态(i)之前回到状态(i)的次数其实就是几何分布，(Geom(p))。

定理11.2.2：回到暂时状态(i)的次数是几何分布。(i)是马尔科夫链的暂时性状态，从(i)出发后无法回到(i)的状态是正值(p)，(p>0)。那么离开状态(i)前，从状态(i)出发又回到状态(i)的次数是几何分布(Geom(p))。

即只要有概率走上不归路，那么它一定会走上不归路，所以才叫暂时性状态。走上不归路前徘徊的次数是几何分布。

方便的话，画出状态转移图如上图，即可对状态进行分类。

定义11.2.3：转移矩阵为(Q)的马尔科夫链，如果对于任意两个状态(i)和(j)，都能在有限的时间步中从状态(i)转移到状态(j)（即转移概率是正值），那么该链就是不可约的（irreducible）链。或者说，对于任意(i)、(j)，存在正整数(n)使得(Q^n)的((i,j))项为正值。不是不可约的马尔科夫链，即可约的（reducible）马尔科夫链。

定理11.2.4：不可约的马尔科夫链的所有状态都是周期性状态。

但是反过来不成立，因为有可能可约的马尔科夫链的所有状态都是周期性的。反例如图。

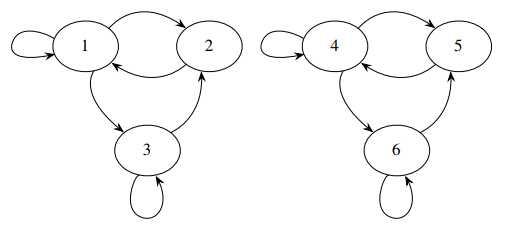
例11.2.5：赌徒的毁灭

例11.2.6：收集优惠券

另一种分类方式是根据状态的持续时间。

定义11.2.8：状态(i)的周期（period），即从状态(i)出发再回到状态(i)的所有可能的步数的最大公约数。如果状态(i)的周期是1，那么状态(i)是非周期性的，否则就是周期性的。如果一个马尔科夫链的所有状态(i)都是非周期性的，那么这条链就是非周期性的。

定理11.2.9：不可约的马尔科夫链的所有状态都有相同的周期。

11.3 Stationary distribution 定常分布/平稳分布

最开始时间，马尔科夫链可能会在暂时性状态中，但最终，马尔科夫链一直都在周期性状态中。那么在每个周期性状态的时间分布是怎么样的？定常分布就是回答这个问题的。

定常分布描述了长期运行中，马尔科夫链在每个定常状态的概率，和待在每个定常状态花的时间。

定义11.3.1：定常状态。对于行向量( extbf{s}=(s_1,s_2,...s_M))，其中(s_i geq 0且 sum_{i}{s_i}=1)，如果对于马尔科夫链的转移矩阵，对于所有(j)存在

[sum_{i}{s_i q_{ij}}=s_i ]

即，

[ extbf{s}Q= extbf{s} ]

那么( extbf{s})就是一个定常分布。

( extbf{s})是(X_0)的分布，那么( extbf{s}Q)是(X_1)的分布，也是( extbf{s})，同样地，(X_2,X_3)分布都是( extbf{s})。即，如果马尔科夫链的初始状态是定常分布，那么永远都是定常分布。

( extbf{s})是(Q)的特征为1的左特征向量。

11.3.1 存在性和唯一性

对于有限状态空间的马尔科夫链，定常分布一定存在。对于不可约的马尔科夫链，定常分布是唯一的。

定理11.3.5：定常分布的存在性和唯一性。对于不可约的马尔科夫链，存在唯一的定常分布，且其中的每个状态都是正的概率。

11.3.2 收敛性

定理11.3.6：(X_0,X_1,...)是不可约、非周期的马尔科夫链，其定常分布是({ extbf{s}})，转移矩阵是(Q)。那么随着(n o infty)，(P(X_n=i))收敛于(s_i)。也就是说(Q^n)收敛于每行都是( extbf{s})的矩阵。

因此，经过一定时间步后，链的状态是状态(i)的概率基本接近定常分布(s_i)。

11.3.3 Google PageRank

11.4 可逆性

通常来说，找到定常分布需要大量的计算，本节介绍了一种特殊情况下不用求特征方程的方法。

定义11.4.1：可逆性。(Q=(q_{ij}))是马尔科夫链的转移方程。( extbf{s}=(s_1,s_2,...,s_M), s_i geq 0, sum_i{s_i}=1)，使得对于所有状态(i,j)成立：

[s_i q_{ij} = s_j q_{ji} ]

这个等式即是可逆性。

定理11.4.2：可逆性意味着定常。

参考：
Introduction to Probability, Second Edition (Chapman & Hall/CRC Texts in Statistical Science)
基本就是这本书第11章的内容