关系数据理论

Posted 2020-10-04 zhouyeqin

写在前面，⊂⊆⊈∈∉符号的区分：

⊂：包含于

⊆：包含于或等于

⊈：不包含于或等于

∈：属于   ∉：不属于

⊂和∈的区别："包含于"用于说明集合与集合之间的关系,"属于"用于说明集合与元素之间的关系。

 

什么是好的关系模式(表结构)？

不好的关系模式会有什么问题？

怎样把不好的关系模式转化为好的？

这就是下面要学的──关系数据库的规范化理论

本节要点：

• 函数依赖
• 码
• 范式
  •  1NF
  •  2NF
  •  3NF

 

首先看4个定义。

1         函数依赖

定义1： 设R(U)是一个属性集U上的关系模式，X和Y是U的子集。若对于R(U)的任意一个可能的关系r，r中对于X的每一个具体值，Y都有唯一的具体值与之对应, 则称 “X函数决定Y” 或  “Y函数依赖于X”，记作X→Y。y=f(x)

X称为这个函数依赖的决定属性集。

等价定义:r中不可能存在两个元组在X上的属性值相等，而在Y上的属性值不等

示例: Student(Sno, Sname, Ssex, Sage, Sdept)

则有:

Sno  → Sname ,   Sno → Ssex，

Sno → Sage ,   Sno → Sdept，

 但Ssex Sage

介绍一些术语：

若X→Y，并且Y→X,  则记为X←→Y。

若Y不函数依赖于X,   则记为X  Y。 

若 X→Y，则X称为这个函数依赖的决定属性组，也称为决定因素。

若X→Y，但Y Í X, 则称X →Y是非平凡的函数依赖。

若X→Y，但Y ⊈ X,   则称X→Y是平凡的函数依赖。对于任一关系模式，平凡函数依赖都是必然成立的，若不特别声明，总是讨论非平凡的函数依赖。

示例：在关系SC(Sno, Cno, Grade)中

平凡函数依赖：   Sno → Sno

 (Sno, Cno) → Sno

 (Sno, Cno) → Cno

非平凡函数依赖： (Sno, Cno) → Grade

定义2：设X,Y是关系R的两个属性集合，X’是X的真子集，存在X→Y，但对每一个X’都有X’!→Y，则称Y完全函数依赖于X。若存在X’→Y，则称Y部分函数依赖于X。

示例：学生成绩表中（学号，课程号）→成绩是完全函数依赖，（学号，课程号）→学生所在系是部分函数依赖，因为学号→学生所在系成立，而学号是（学号，课程号）的真子集。

定义3：设X,Y,Z是关系R中互不相同的属性集合，存在X→Y(Y!→X),Y→Z，则称Z传递函数依赖于X。

注：如果Y→X，即X←→Y，则Z直接依赖于X。

示例：在关系R(学号 ,宿舍, 费用)中，(学号)->(宿舍),宿舍！=学号，(宿舍)->(费用),费用!=宿舍，所以符合传递函数的要求。

2         码

第二章关于候选码（Candidate key）的定义:若关系中的某一属性组的值能唯一地标识一个元组，则称该属性组为候选码，候选码简称为码。

         定义4：设K为关系模式R<U,F>中的属性或属性组合。若U对K完全依赖，则K为R的候选码。若关系某事R有多个候选码，则选定其中一个为主码（Primary key）。

         主属性与非主属性：包含在任何一个候选码中的属性称为主属性，不包含在任何码中的属性称为非主属性。

         全码（All Key）：一个关系中所有属性的组合为码，称为全码。

 

然后研究数据库的规范化。

3         范式

关系数据库中的关系是要满足一定要求的，满足不同程度要求的为不同范式。满足最低要求的叫第一范式，简称1NF。在第一范式中满足进一步要求的为第二范式，其余以此类推。

范式的种类：（这里仅学习前三种） 

                            第一范式(1NF)

                            第二范式(2NF)

                            第三范式(3NF)

                            BC范式(BCNF)

                            第四范式(4NF)

                            第五范式(5NF)

各范式之间的关系：5NF⊂4NF⊂3NF ⊂2NF ⊂1NF。

3.1       1NF

定义5：如果一个关系模式R的所有属性都是不可分的基本数据项，则R∈1NF。

回忆关系的性质：

① 列是同质的

② 不同的列可出自同一个域

③ 列的顺序无所谓

④ 任意两个元组不能完全相同

⑤ 行的顺序无所谓

⑥ 分量必须取原子值

如下面关系中，一个学生需要学习多门课程，所以一个属性里面包含多个值，不符合“⑥分量必须取原子值”的性质。所以不满足1NF。

关系模式：SCG(SNO, SNAME, SAGE,  CNO,  GRADE)

 

改成下面样式，使关系满足1NF：

 

 

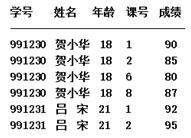
3.2       2NF

上面满足1NF的关系可能存在的问题：

1.数据冗余：贺小华学生的基本信息进行了多次保存

2.修改困难：如果想修改“贺小华”为“贺大华”则需要更改4次，而且要保证没有遗漏

3.插入和删除异常--该插入的不能插，不该删的删了：当前关系是以学号和课程号作为主码，那么如果仅仅只想插入一条学生信息就不能实现，因为没有课号信息。

 

那么怎么才能规避这些问题呢？

分析上述关系的函数依赖。

关系模式：SCG(SNO, SNAME, SAGE,  CNO,  GRADE)

函数依赖包括：

         GRADE对（SNO, CNO）完全函数依赖

SNAME 依赖于SNO

SNAME对（SNO, CNO）部分函数依赖

同样SAGE依赖于SNO

SAGE对（SNO, CNO）部分函数依赖

         分析上面的例子，可以发现问题在于有两种非主属性。一种如GRADE，它对码是完全函数依赖。另一种如SNAME，SAGE对码不是完全函数依赖。所以解决1NF这些问题就是使所有非主属性完全依赖于码。

         定义6：若关系模式R∈1NF，并且每一个非主属性都完全函数依赖于R的 码，则R∈2NF。(2NF也就是不允许关系模式存在非主属性对码的部分函数依赖)

所以SCG(SNO, SNAME, SAGE, CNO, GRADE)不属于2NF。

解决办法：

         SCG分解为两个关系模式

S(SNO, SNAME, SAGE)

SC（SNO， CNO， GRADE）

S： SNO→SNAME    SNO→SAGE

SC:（SNO， CNO） → GRADE

没有非主属性对码部分函数依赖S，SC分别达到2NF，1NF的3个问题也得到解决。

3.3       3NF

有关系模式 SL(Sno, Sname, Sdept, Sloc)表示学生的信息和系地址信息。

关系如下：

Sno	Sname	Sdept	Sloc
95001	李勇	CS	理科楼
95002	刘晨	CS	理科楼
95003	王敏	CS	理科楼
95004	张立	IS	文科楼
95005	刘斌	IS	文科楼
95006	王建国	IS	文科楼
95007	王家昌	MA	综合楼

存在问题：

1)       数据冗余度大：每个系的地址都一样，关于系地址的信息却要重复存储于该系学生人数相同的次数。

2)       修改困难：当学校调整系地址时，每个系地址的信息重复存储，修改时必须同时更新该系所有学生的Sloc

3)       插入异常：如果某个系刚成立，目前暂时没有在校学生，无法把系地址的信息存入数据库。

4)       删除异常：如果某个系的学生全部毕业了，在删除该系学生信息的同时，把这个系的地址信息也删除了。

问题出在哪呢？

存在非主属性对码的传递依赖：（Sloc不直接依赖于码Sno，而是通过Sdept传递依赖）

          Sno→Sdept

          Sdept→ Sloc

          Sno→ Sloc

定义7： 关系模式R<U，F> 中若不存在这样的码X、属性组Y及非主属性Z, 使得X→Y，Y → Z成立，则称R<U，F> ∈ 3NF。 （即没有非主属性对码的传递函数依赖）

例， SL(Sno, Sname, Sdept, Sloc )∈2NF

     SL(Sno, Sname, Sdept, Sloc ) ∉ 3NF

解决方法：

把SL分解为两个关系模式，以消除传递函数依赖：

          SD（Sno， Sname,  Sdept）

          DL（Sdept， Sloc）

SD的码为Sno，DL的码为Sdept。非主属性直接依赖于码,是3NF，2NF存在的几个问题得到解决。

若R∈3NF，则R的每一个非主属性，既不部分函数依赖于码，也不传递函数依赖于码。