用OpenGL进行曲线曲面的绘制

Posted 2020-10-03 ~不会飞的章鱼~

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了用OpenGL进行曲线曲面的绘制相关的知识，希望对你有一定的参考价值。

实验目的

理解Bezier曲线、曲面绘制的基本原理；理解OpenGL中一维、二维插值求值器的用法。
掌握OpenGL中曲线、曲面绘图的方法，对比不同参数下的绘图效果差异；

代码1：用四个控制点绘制一条三次Bezier曲线

#include "stdafx.h"
#include <stdlib.h>
#include <time.h>
#include <GL/glut.h>

//4个控制点的3D坐标——z坐标全为0
GLfloat ctrlpoints[4][3] = {
    { -4, -4, 0 }, { -2, 4, 0 }, { 2, -4, 0 }, { 4, 4, 0 }
};

void init(void)
{
    //背景色
    glClearColor(0.0, 0.0, 0.0, 1.0);
    //将控制点坐标映射为曲线坐标
    //参数1：GL_MAP1_VERTEX_3，3维点坐标
    //参数2和3：控制参数t或u的取值范围[0, 1]
    //参数4：曲线内插值点间的步长3————3维坐标
    //参数5：曲线间的补偿为顶点数4个————总步长为12
    //参数6：控制点二维数组首元素地址
    //注意: 若是在这里设置了相关参数，后续对ctrlpoints内容更改曲线不变
    glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
    //打开开关——允许3维坐标控制点到参数点转换开关
    glEnable(GL_MAP1_VERTEX_3);
    glShadeModel(GL_FLAT);

    //代码开关2：去掉本注释，可启用反走样
    /*
    glEnable(GL_BLEND);
    glEnable(GL_LINE_SMOOTH);  //允许直线反走样
    glHint(GL_LINE_SMOOTH_HINT, GL_FASTEST);  // Antialias the lines
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
    */
}

void display(void)
{
    int i;
    glClear(GL_COLOR_BUFFER_BIT);
    glColor3f(1.0, 1.0, 1.0);

    //代码开关1：去掉本注释，查看动态的曲线绘图效果：动态更新控制点坐标
    /*
    for(int t = 0; t < 4; t++) {
    for(int j = 0; j < 3; j++)
    ctrlpoints[t][j] = (rand() % 1024 / 1024.0 - 0.5) * 10;
    }
    //动态映射
    glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
    */
    glLoadIdentity();
    glColor3f(1.0, 0.0, 0.0);
    //绘制连续线段
    glBegin(GL_LINE_STRIP);
    //参数t或u取值为i/30，共计31个点
    for (i = 0; i <= 30; i++)
        glEvalCoord1f((GLfloat)i / 30.0);   //根据4个控制点坐标的参数化插值
    glEnd();
    /* 显示控制点 */
    glPointSize(5.0);
    glBegin(GL_POINTS);
    for (i = 0; i < 4; i++)
        glVertex3fv(&ctrlpoints[i][0]);
    glEnd();

    glTranslatef(-0.1f, 0.1f, 0.0f);
    glColor3f(0.0, 1.0, 0.0);
    //glLineWidth(2.0);
    //绘制连续线段——线段数越多，曲线越光滑
    glBegin(GL_LINE_STRIP);
    //设置参数t或u取值为i/60，共计61个点
    //实验：若让t从-2变化到+2，可看到什么效果
    for (i = 0; i <= 60; i++)
        glEvalCoord1f((GLfloat)i / 60.0);  //根据4个控制点坐标的参数化插值
    glEnd();

    glTranslatef(-0.1f, 0.1f, 0.0f);
    glColor3f(1.0, 1.0, 1.0);
    //绘制连续线段
    glBegin(GL_LINE_STRIP);
    //设置参数t或u取值为i/60，共计61个点
    //实验：若让t从-2变化到+2，可看到什么效果
    for (i = 0; i <= 100; i++)
        glEvalCoord1f((GLfloat)i / 100.0);
    glEnd();

    glutSwapBuffers();
}

//3D空间中绘制2D效果，采用正交投影
void reshape(GLsizei w, GLsizei h)
{
    glViewport(0, 0, w, h);

    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    if (w <= h)
        glOrtho(-5.0, 5.0, -5.0*(GLfloat)h / (GLfloat)w, 5.0*(GLfloat)h / (GLfloat)w, -5.0, 5.0);
    else
        glOrtho(-5.0*(GLfloat)w / (GLfloat)h, 5.0*(GLfloat)w / (GLfloat)h, -5.0, 5.0, -5.0, 5.0);

    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
}

void keyboard(unsigned char key, int x, int y)
{
    switch (key)
    {
    case \'x\':
    case \'X\':
    case 27:   //ESC键
        exit(0);
        break;
    default:
        break;
    }
}

int main(int argc, char** argv)
{
    srand((unsigned int)time(0));
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);//使用双缓存模式和深度缓存
    glutInitWindowSize(800, 800);
    glutInitWindowPosition(0, 0);
    glutCreateWindow("2D Bezier曲线");
    init();
    glutDisplayFunc(display);
    glutReshapeFunc(reshape);
    glutKeyboardFunc(keyboard);
    glutIdleFunc(display);//设置空闲时调用的函数
    glutMainLoop();
    return 0;
}

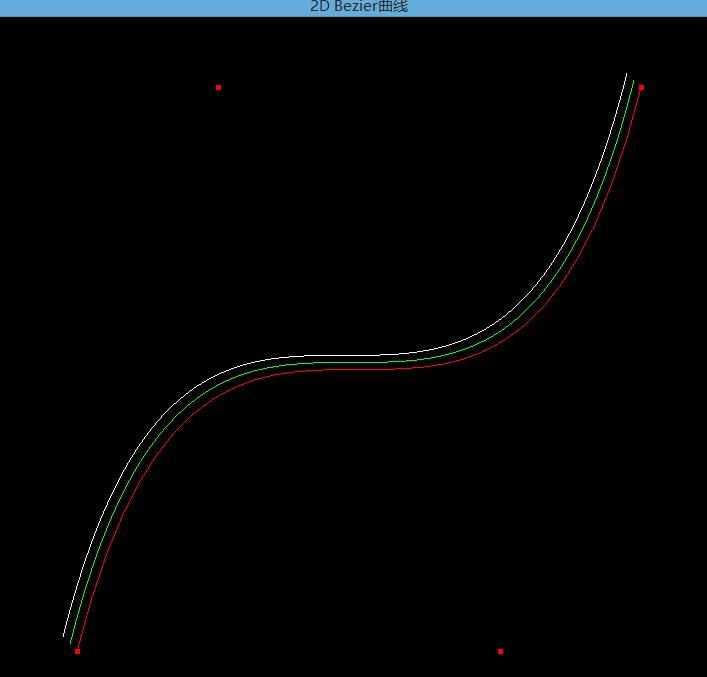
此时我们打开代码开关1，查看动态Bezier曲线绘制效果：

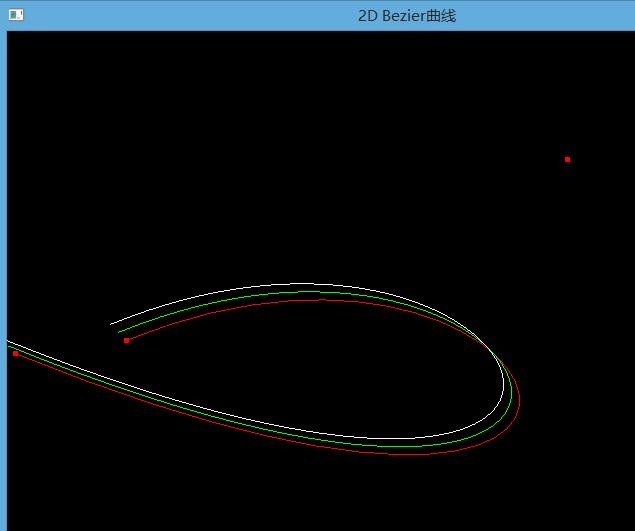
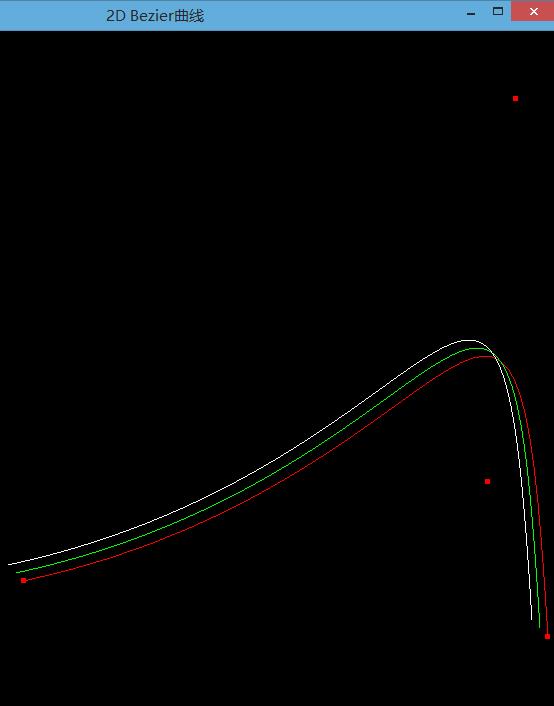
关闭代码开关1，打开代码开关2，查看直线反走样效果：

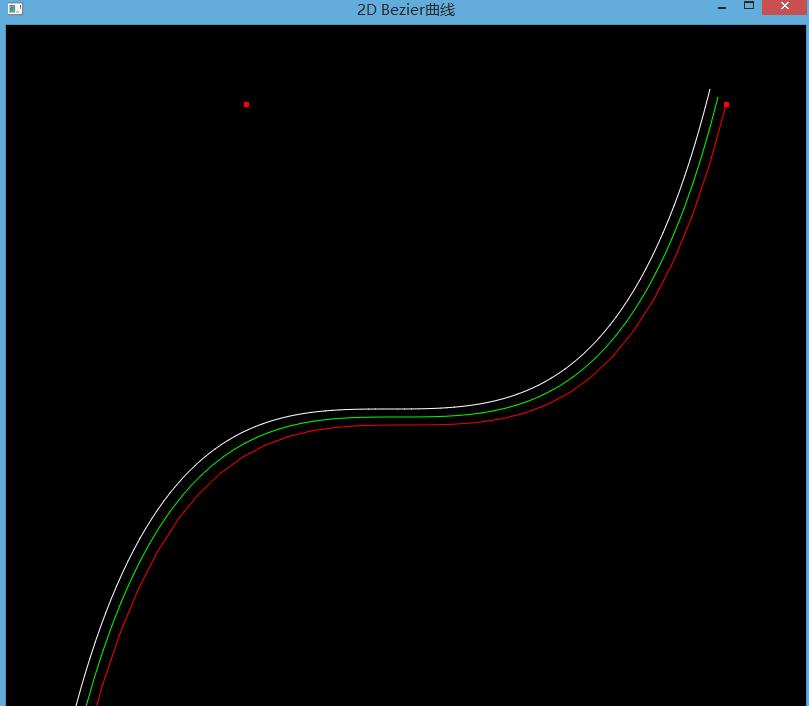
对比刚开始的效果图，我们发现，使用了直线反走样后，绘制出的曲线很光滑，看着很舒服。

**代码2：用4*4个控制点绘制一个三次Bezier曲面线框模型**

Github地址

#include "stdafx.h"
#include <stdlib.h>
#include <time.h>
#include <GL/glut.h>

/* 控制点的坐标 */
GLfloat ctrlpoints[4][4][3] = {
    { { -1.5, -1.5, 2.0 },
    { -0.5, -1.5, 2.0 },
    { 0.5, -1.5, -1.0 },
    { 1.5, -1.5, 2.0 }
    },

    { { -1.5, -0.5, 1.0 },
    { -0.5, 1.5, 2.0 },
    { 0.5, 0.5, 1.0 },
    { 1.5, -0.5, -1.0 } },

    { { -1.5, 0.5, 2.0 },
    { -0.5, 0.5, 1.0 },
    { 0.5, 0.5, 3.0 },
    { 1.5, -1.5, 1.5 } },

    { { -1.5, 1.5, -2.0 },
    { -0.5, 1.5, -2.0 },
    { 0.5, 0.5, 1.0 },
    { 1.5, 1.5, -1.0 } } };

void init(void)
{
    //背景色
    glClearColor(0.0, 0.0, 0.0, 1.0);
    //将控制点坐标映射为曲面坐标
    //参数1：GL_MAP1_VERTEX_3，3维点坐标
    //参数2和3：控制参数u的取值范围[0, 1]
    //参数4：x方向元素间的步长为3个GLfloat
    //参数5：x方向曲线间的步长为4个控制点——曲线由4个控制点确定
    //参数6-7：控制参数v的取值范围[0, 1]
    //参数8：y方向元素间的步长为12个GLfloat元素
    //参数9：y方向每条曲线的控制点数量为4
    //注意: 若是在这里设置了相关参数，后续对ctrlpoints内容更改曲线不变
    glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4, 0, 1, 12, 4, &ctrlpoints[0][0][0]);
    //允许二维映射
    glEnable(GL_MAP2_VERTEX_3);
    //二维映射：x、y方向U和V的参数[0, 1]，且中间插值数量为各20个
    glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);
    //允许深度测试
    glEnable(GL_DEPTH_TEST);

    //代码开关2：启用反走样
    glEnable(GL_BLEND);
    glEnable(GL_LINE_SMOOTH);
    glHint(GL_LINE_SMOOTH_HINT, GL_FASTEST);  // Antialias the lines
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
}

void display(void)
{
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    glColor3f(0.0, 1.0, 0.0);
    glPushMatrix();
    //代码开关1：去掉注释查看效果；更改旋转角度参数，查看效果
    //glRotatef(0.1, 1.0, 1.0, 1.0);
    int i, j;
    //生成2D网格坐标，以从控制点参数插值确定网格点所对应的点集所对应的坐标
    for (j = 0; j <= 8; j++)     {
        glBegin(GL_LINE_STRIP);
        for (i = 0; i <= 30; i++)
            glEvalCoord2f((GLfloat)i / 30.0, (GLfloat)j / 8.0);  //固定y坐标时x方向的网格坐标
        glEnd();

        glBegin(GL_LINE_STRIP);
        for (i = 0; i <= 30; i++)
            glEvalCoord2f((GLfloat)j / 8.0, (GLfloat)i / 30.0);  //固定x坐标时y方向的网格坐标     
        glEnd();
    }

    //查看网格所确定的插值点(u, v)的位置
    glColor3f(1, 0, 0);
    glBegin(GL_POINTS);
    for (j = 0; j <= 8; j++)     {
        for (i = 0; i <= 30; i++)
            glVertex3f((GLfloat)i / 30.0, (GLfloat)j / 8.0, 0);
        for (i = 0; i <= 30; i++)
            glVertex3f((GLfloat)j / 8.0, (GLfloat)i / 30.0, 0);
    }
    glEnd();
    glPopMatrix();
    glutSwapBuffers();
}

void reshape(GLsizei w, GLsizei h)
{
    glViewport(0, 0, w, h);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    if (w <= h)
        glOrtho(-5.0, 5.0, -5.0*(GLfloat)h / (GLfloat)w, 5.0*(GLfloat)h / (GLfloat)w, -5.0, 5.0);
    else
        glOrtho(-5.0*(GLfloat)w / (GLfloat)h, 5.0*(GLfloat)w / (GLfloat)h, -5.0, 5.0, -5.0, 5.0);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
}

void keyboard(unsigned char key, int x, int y)
{
    switch (key)
    {
    case \'x\':
    case \'X\':
    case 27:   //ESC键
        exit(0);
        break;
    default:
        break;
    }
}

int main(int argc, char** argv)
{
    srand((unsigned int)time(0));
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);//使用双缓存模式和深度缓存
    glutInitWindowSize(800, 800);
    glutInitWindowPosition(0, 0);
    glutCreateWindow("Bezier曲面线框模型");
    init();
    glutDisplayFunc(display);
    glutReshapeFunc(reshape);
    glutKeyboardFunc(keyboard);
    glutIdleFunc(display);//设置空闲时调用的函数
    glutMainLoop();
    return 0;
}

打开代码开关1后的效果：

**代码3：用4*4个控制点绘制一个三次Bezier曲面并添加光照效果**

Github地址

#include "stdafx.h"
#include <stdlib.h>
#include <time.h>
#include <GL/glut.h>
/* 控制点的坐标 */
GLfloat ctrlpoints[4][4][3] = {
    { { -1.5, -1.5, 2.0 },
    { -0.5, -1.5, 2.0 },
    { 0.5, -1.5, -1.0 },
    { 1.5, -1.5, 2.0 } },

    { { -1.5, -0.5, 1.0 },
    { -0.5, 1.5, 2.0 },
    { 0.5, 0.5, 1.0 },
    { 1.5, -0.5, -1.0 } },

    { { -1.5, 0.5, 2.0 },
    { -0.5, 0.5, 1.0 },
    { 0.5, 0.5, 3.0 },
    { 1.5, -1.5, 1.5 } },

    { { -1.5, 1.5, -2.0 },
    { -0.5, 1.5, -2.0 },
    { 0.5, 0.5, 1.0 },
    { 1.5, 1.5, -1.0 } } };

void init(void)
{
    //背景色
    glClearColor(0.0, 0.0, 0.0, 1.0);
    //将控制点坐标映射为曲面坐标
    //参数1：GL_MAP1_VERTEX_3，3维点坐标
    //参数2和3：控制参数u的取值范围[0, 1]
    //参数4：x方向元素间的步长为3个GLfloat
    //参数5：x方向曲线间的步长为4个控制点——曲线由4个控制点确定
    //参数6-7：控制参数v的取值范围[0, 1]
    //参数8：y方向元素间的步长为12个GLfloat元素
    //参数9：y方向每条曲线的控制点数量为4
    //note: 若是在这里设置了相关参数，后续对ctrlpoints内容更改曲线不变
    glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4, 0, 1, 12, 4, &ctrlpoints[0][0][0]);
    //允许二维映射
    glEnable(GL_MAP2_VERTEX_3);
    //二维映射：x、y方向U和V的参数[0, 1]，且中间插值数量为各20个
    glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);
    //允许深度测试
    glDepthFunc(GL_LESS);
    glEnable(GL_DEPTH_TEST);
    //代码开关4：取消下面两行代码，查看曲面显示效果差异
    //打开自动法矢量开关
    //glEnable(GL_AUTO_NORMAL);
    //允许正则化法矢量
    //glEnable(GL_NORMALIZE);

    //代码开关3：设置材质与光源
    GLfloat ambient[] = { 0.4, 0.6, 0.2, 1.0 };
    GLfloat position[] = { 0.0, 1.0, 3.0, 1.0 };
    GLfloat mat_diffuse[] = { 0.2, 0.4, 0.8, 1.0 };
    GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };
    GLfloat mat_shininess[] = { 80.0 };
    glEnable(GL_LIGHTING);
    glEnable(GL_LIGHT0);
    glLightfv(GL_LIGHT0, GL_AMBIENT, ambient);
    glLightfv(GL_LIGHT0, GL_POSITION, position);
    glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
    glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
    glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);
}

void display(void)
{
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    glColor3f(0.0, 1.0, 0.0);
    //如果不希望旋转，则启用push和pop矩阵命令，并注释掉glRotatef行
    //glPushMatrix();
    //代码开关1：去掉注释查看效果；更改旋转角度参数，查看效果
    glRotatef(1.0, 1.0, 1.0, 1.0);
    glEvalMesh2(GL_FILL, 0, 20, 0, 20);
    //glPopMatrix();
    glutSwapBuffers();
}

void reshape(GLsizei w, GLsizei h)
{
    glViewport(0, 0, w, h);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    if (w <= h)
        glOrtho(-5.0, 5.0, -5.0*(GLfloat)h / (GLfloat)w, 5.0*(GLfloat)h / (GLfloat)w, -5.0, 5.0);
    else
        glOrtho(-5.0*(GLfloat)w / (GLfloat)h, 5.0*(GLfloat)w / (GLfloat)h, -5.0, 5.0, -5.0, 5.0);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
}

void keyboard(unsigned char key, int x, int y)
{
    switch (key)
    {
    case \'x\':
    case \'X\':
    case 27:   //ESC键
        exit(0);
        break;
    default:
        break;
    }
}

int main(int argc, char** argv)
{
    srand((unsigned int)time(0));
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);//使用双缓存模式和深度缓存
    glutInitWindowSize(800, 800);
    glutInitWindowPosition(0, 0);
    glutCreateWindow("Bezier曲面");
    init();
    glutDisplayFunc(display);
    glutReshapeFunc(reshape);
    glutKeyboardFunc(keyboard);
    glutIdleFunc(display);//设置空闲时调用的函数
    glutMainLoop();
    return 0;
}

说明

从贝塞尔到B样条

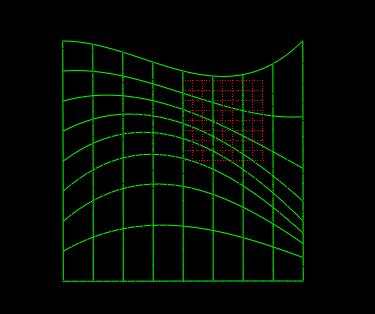
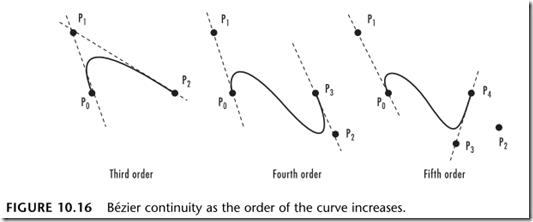
　　贝塞尔曲线由起点、终点和其他控制点来影响曲线的形状。在二次贝塞尔曲线和三次贝塞尔曲线中，可以通过调整控制点的位置而得到很好的平滑性（C2级连续性曲率级）的曲线。当增加更多的控制点的时候，这种平滑性就被破坏了。如下图所示，前两个曲线很平滑（曲率级的连续性），第三个曲线在增加了一个控制点之后，曲线被拉伸了，其平滑性遭到了破坏。

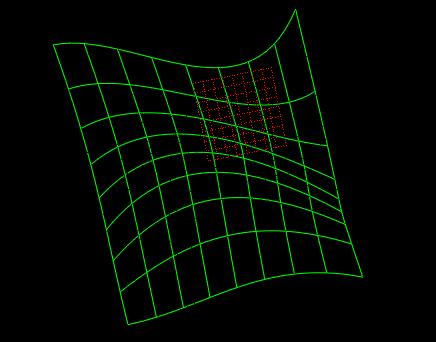
　　B样条的工作方式类似于贝塞尔曲线，但不同的是曲线被分成很多段。每段曲线的形状只受到最近的四个控制点的影响，这样曲线就像是4阶的贝塞尔曲线拼接起来的。这样很长的有很多控制点的曲线就会有固定的连续性，平滑性（每一段都是c2级的连续性）。

结点

　　NURBS（非均匀有理B样条）的真正威力在于，可以调整任意一段曲线中的四个控制点的影响力，来产生较好的平滑性。这是通过一系列结点来控制的。每个控制点都定义了两个结点的值。结点的取值范围是u或v的定义域，而且必须是非递减的。

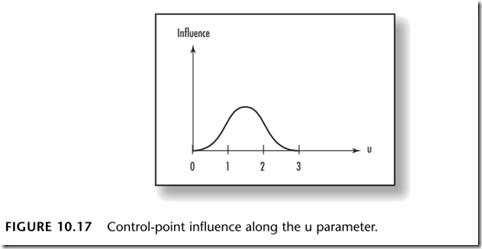
　　结点的值决定了落在u、v参数定义域内的控制点的影响力。下图的曲线表示控制点对一条在u参数定义域内的具有四个单位的曲线的影响。下图表示中间点对曲线的影响更大，而且只有在[0,3]范围内的控制点才会对曲线产生影响。

　在u、v参数定义域内的控制点对曲线的形状会有有影响，而且我们可以通过结点来控制控制点的影响力。非均匀性就是指一个控制点的影响力的范围是可以改变的。

节点 ( Knot ) 是一个 ( 阶数 + N - 1 ) 的数字列表，N 代表控制点数目。有时候这个列表上的数字也称为节点矢量 ( Knot Vector )，这里的矢量并不是指 3D 方向。

节点列表上的数字必须符合几个条件，确定条件是否符合的标准方式是在列表序列中，数字必需维持不变或变大，而且数字重复的次数不可以比阶数大。例如，阶数 3 有 15 个控制点的 NURBS 曲线，列表数字为 0,0,0,1,2,2,2,3,7,7,9,9,9 是一个符合条件的节点列表。列表数字为 0,0,0,1,2,2,2,2,7,7,9,9,9 则不符合，因为此列表中有四个 2，而四比阶数大 ( 阶数为 3 )。

节点值重复的次数称为节点的重数 ( Multiplicity )，在上面例子中符合条件的节点列表中，节点值 0 的重数值为三；节点值 1 的重数值为一；节点值 2 的重数为三；节点值 7 的重数值为二；节点值 9 的重数值为三。

如果节点值重复的次数和阶数一样，该节点值称为全复节点 ( Full-Multiplicity Knot )。在上面的例子中，节点值 0、2、9 有完整的重数，只出现一次的节点值称为单纯节点 ( Simple Knot )，节点值 1 和 3 为单纯节点。

如果在节点列表中是以全复节点开始，接下来是单纯节点，再以全复节点结束，而且节点值为等差，称为均匀 ( Uniform )。例如，如果阶数为 3 有 7 个控制点的 NURBS 曲线，其节点值为 0,0,0,1,2,3,4,4,4，那么该曲线有均匀的节点。如果节点值是 0,0,0,1,2,5,6,6,6 不是均匀的，称为非均匀 ( Non-Uniform )。在 NURBS 的 NU 代表“非均匀”，意味着在一条 NURBS 曲线中节点可以是非均匀的。

在节点值列表中段有重复节点值的 NURBS 曲线比较不平滑，最不平滑的情形是节点列表中段出现全复节点，代表曲线有锐角。因此，有些设计师喜欢在曲线插入或移除节点，然后调整控制点，使曲线的造型变得平滑或尖锐。因为节点数等于 ( N + 阶数 - 1 )，N 代表控制点的数量，所以插入一个节点会增加一个控制点，移除一个节点也会减少一个控制点。插入节点时可以不改变 NURBS 曲线的形状，但通常移除节点必定会改变 NURBS 曲线的形状。

节点（Knot）与控制点关系：控制点和节点是一对一成对的是常见的错误概念，这种情形只发生在 1 阶的 NURBS ( 多重直线 )。较高阶数的 NURBS 的每 ( 2 x 阶数 ) 个节点是一个群组，每 ( 阶数 + 1 ) 个控制点是一个群组。例如，一条 3 阶 7 个控制点的 NURBS 曲线，节点是 0,0,0,1,2,5,8,8,8，前四个控制点是对应至前六个节点；第二至第五个控制点是对应至第二至第七个节点 0,0,1,2,5,8；第三至第六个控制点是对应至第三至第八个节点 0,1,2,5,8,8；最后四个控制点是对应至最后六个节点

重要：NURB曲面上的裁剪、细分、镶嵌效果，查看网页 https://my.oschina.net/sweetdark/blog/184313

**代码4：用4*4个控制点绘制一个NURBS曲面并添加光照效果**

Github地址

#include "stdafx.h"
#include <stdlib.h>怎样用WPF绘制简单的三维曲线?
 MATLAB | 如何绘制三维曲线曲面多边形投影(三视图)？
 MATLAB | 如何绘制三维曲线曲面多边形投影(三视图)？
 6种常见三维曲面的Three.js实现
 GLSL片段着色器 - 绘制简单的粗曲线
 Matlab随笔之画图函数总结