[BZOJ 1043] 下落的圆盘

Posted 2020-10-02

题意

　　有 n 个圆 {(x[i], y[i], r[i])} 依次下落到平面.

　　问没有被覆盖的圆的轮廓总长.

　　n <= 1000.

 

分析

　　枚举之后的圆, 算当前圆被覆盖的弧度.

　　对被每个圆覆盖的弧度区间取并.

 

　　圆之间的关系有: 内含, 内切, 相交, 外切, 相离. 特别地, 这里还需要考虑圆的顺序.

　　我们画出了所有的情况, 然后分类处理.

　　　　　　　　　　　　

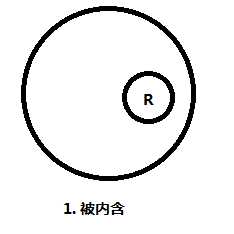
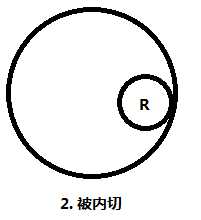
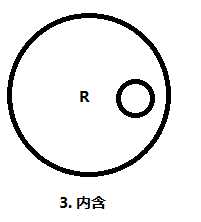
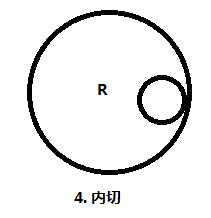
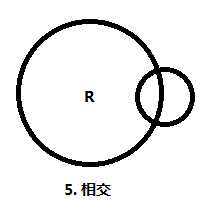
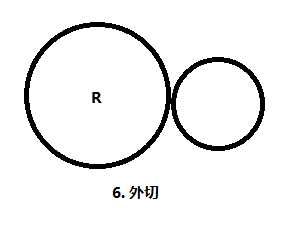
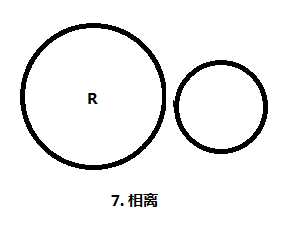
　　不妨设当前计算的圆为 (x, y, r) , 影响它的圆为 (x1, y1, r1) .

　　①②: 若 (x - x1)(x - x1) + (y - y1)(y - y1) <= (r - r1)(r - r1) 且 r <= r1 , 则 (x, y, r) 完全被覆盖.

　　⑤: 若 (r - r1)(r - r1) < (x - x1)(x - x1) + (y - y1)(y - y1) < (r + r1)(r + r1) , 则我们可以算出被覆盖的弧度.

　　③④⑥⑦: 否则, 不产生任何影响.

 

　　我们可以尝试用代数方法算出两个圆的交点: 先将解析式展开, 然后相减得到一条一次的式子, 代入其中一个圆的解析式.

　　知道了交点 (p, q) 之后, 我们可以直接用 atan2((q - y) / r, (p - x) / r) 算出对应的弧度.

　　但是这种算法有些难推导.

 

　　我们尝试直接算角度.

　　　　

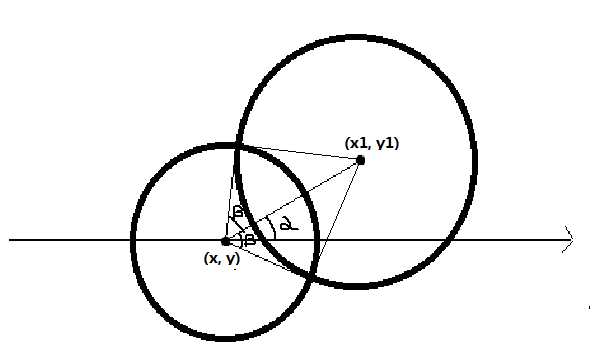
　　α 可以通过 atan2(y1 - y, x1 - x) 算出.

　　β 可以通过 余弦定理 + acos 算出.

　　

　　得到弧度区间 [L, R] , L = α - β , R = α + β .

　　将 [L, R] 标准化到 [-π, +π] , 如果 L > R , 那么拆分成两个区间.

 

实现

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <cstdlib>
 4 #include <cctype>
 5 #include <cmath>
 6 #include <algorithm>
 7 using namespace std;
 8 #define F(i, a, b) for (register int i = (a); i <= (b); i++)
 9 #define db double
10 
11 const db EPS = 1e-7;
12 inline int sign(db x) { return fabs(x) < EPS ? 0 : x < 0 ? -1 : 1; }
13 inline int cmp(db x, db y) { return sign(x - y); }
14 
15 const int N = 2005;
16 const db PI = acos(-1);
17 const db INF = 1e20;
18 
19 int n;
20 struct C { db x, y, r; }c[N];
21 
22 int tot;
23 struct Int {
24     db l, r;
25     friend inline bool operator < (Int A, Int B) { return cmp(A.l, B.l) < 0; }
26 }itv[N];
27 db sum;
28 
29 inline db Std(db &x) {
30     while (cmp(x, -PI) < 0) x += 2 * PI;
31     while (cmp(x, +PI) > 0) x -= 2 * PI;
32 }
33 db Calc(int ID) {
34     tot = 0;
35     db x = c[ID].x, y = c[ID].y, r = c[ID].r;
36     F(i, ID+1, n) {
37         db x1 = c[i].x, y1 = c[i].y, r1 = c[i].r;
38         db D = (x - x1) * (x - x1) + (y - y1) * (y - y1);    // Dist
39         db M = (r - r1) * (r - r1), P = (r + r1) * (r + r1);    // Minus ^ 2, Plus ^ 2
40         
41         if (cmp(D, M) <= 0 && cmp(r, r1) <= 0) return 0;
42         else if (cmp(M, D) < 0 && cmp(D, P) < 0) {
43             db A = atan2(y1 - y, x1 - x);
44             db B = acos((r * r + D - r1 * r1) / (2 * r * sqrt(D)));
45             db L = A - B, R = A + B;
46             Std(L), Std(R);
47             if (cmp(L, R) < 0)
48                 itv[++tot] = (Int){L, R};
49             else itv[++tot] = (Int){L, +PI}, itv[++tot] = (Int){-PI, R};
50         }
51         // [-PI, +PI], -PI = +PI
52     }
53     sort(itv+1, itv+tot+1);
54     
55     db cnt = 0, L = -INF, R = -INF;
56     F(i, 1, tot) {
57         if (cmp(R, itv[i].l) < 0) cnt += R-L, L = itv[i].l;
58         R = max(R, itv[i].r);
59     }
60     return (2 * PI - (cnt + R - L)) * r;
61 }
62 
63 int main(void) {
64     #ifndef ONLINE_JUDGE
65         freopen("bzoj1043.in", "r", stdin);
66     #endif
67     
68     scanf("%d", &n);
69     F(i, 1, n) {
70         db x, y, r;
71         scanf("%lf %lf %lf", &r, &x, &y);
72         c[i] = (C){x, y, r};
73     }
74     
75     F(i, 1, n)
76         sum += Calc(i);
77     printf("%0.3lf\\n", sum - EPS);
78     
79     return 0;
80 }