『cs231n』无监督学习

Posted 2020-10-02 叠加态的猫

传统自编码器，变分自编码器，gen网络

经典无监督学习

聚类

K均值

PCA主成分分析

等

深度学习下的无监督学习

• 自编码器
  • 传统的基于特征学习的自编码器
  • 变种的生成式自编码器
• Gen网络（对抗式生成网络）

 

传统自编码器

原理

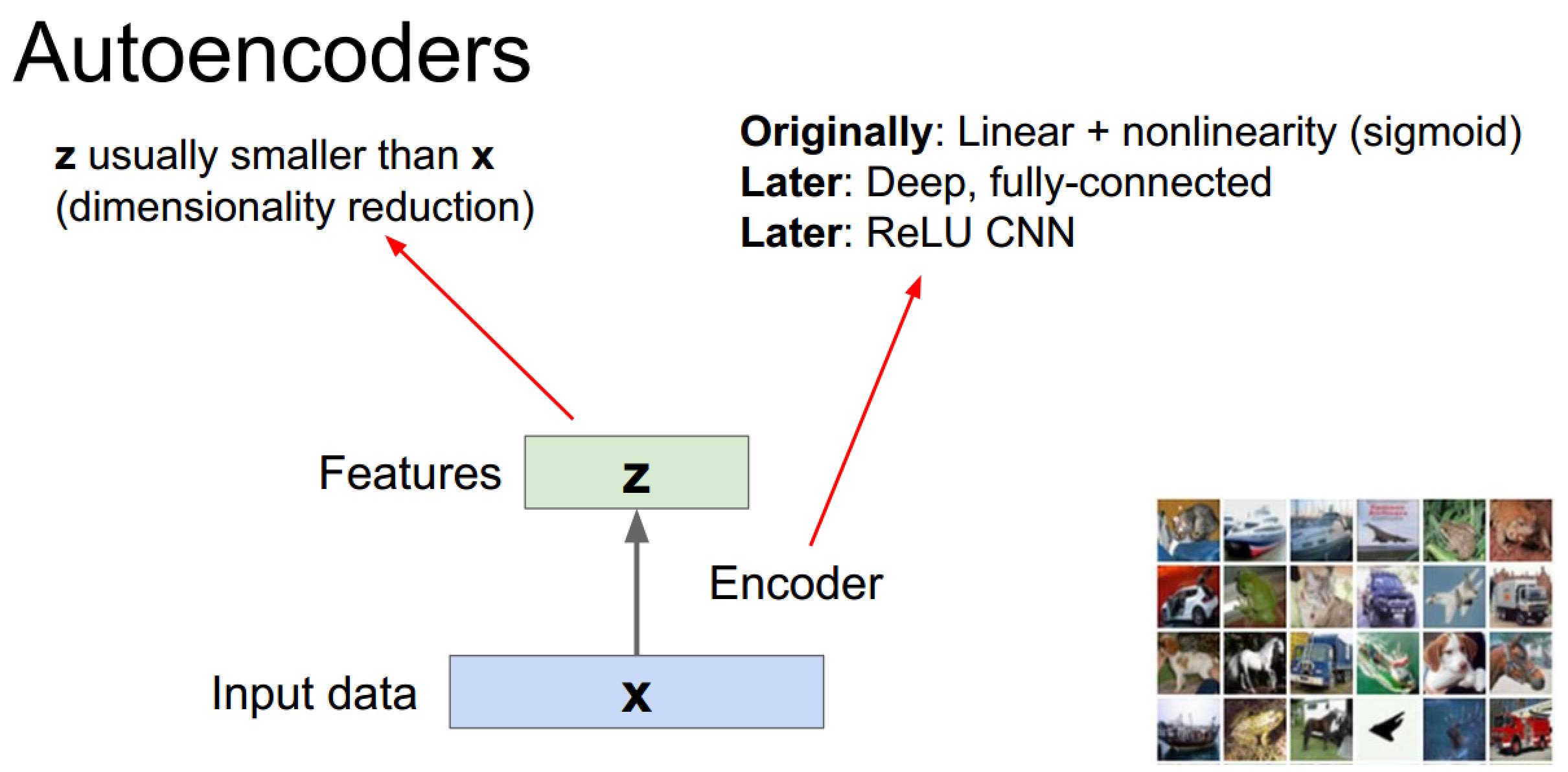
类似于一个自学习式PCA，如果编码/解码器只是单层线性的话

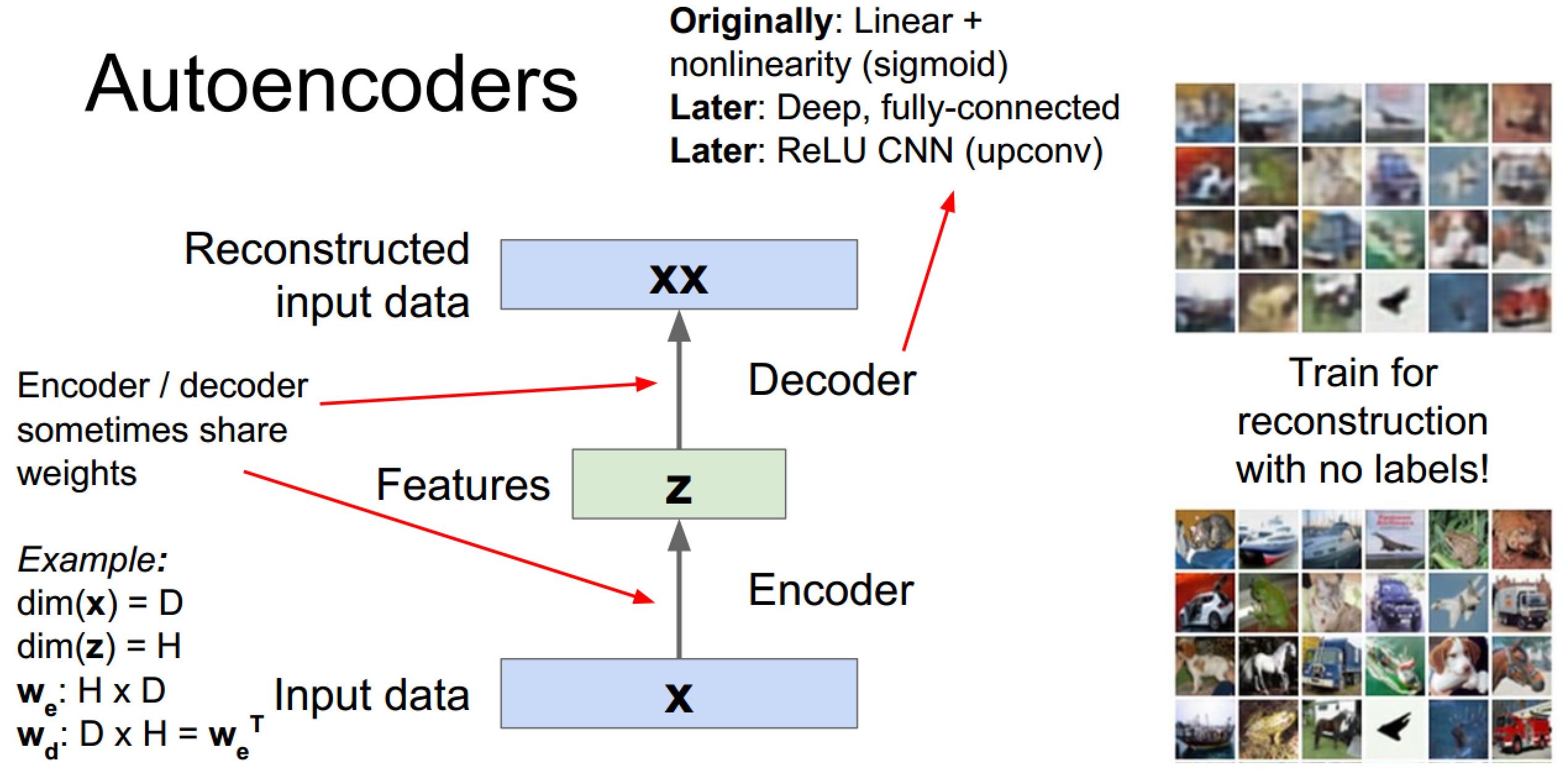
自编码器编码解码示意图：

特征提取过程中甚至用到了卷积网络+relu的结构（我的认知停留在Originally级别）

编码&解码器可以共享权值（在我接触的代码中一般都没共享权值）

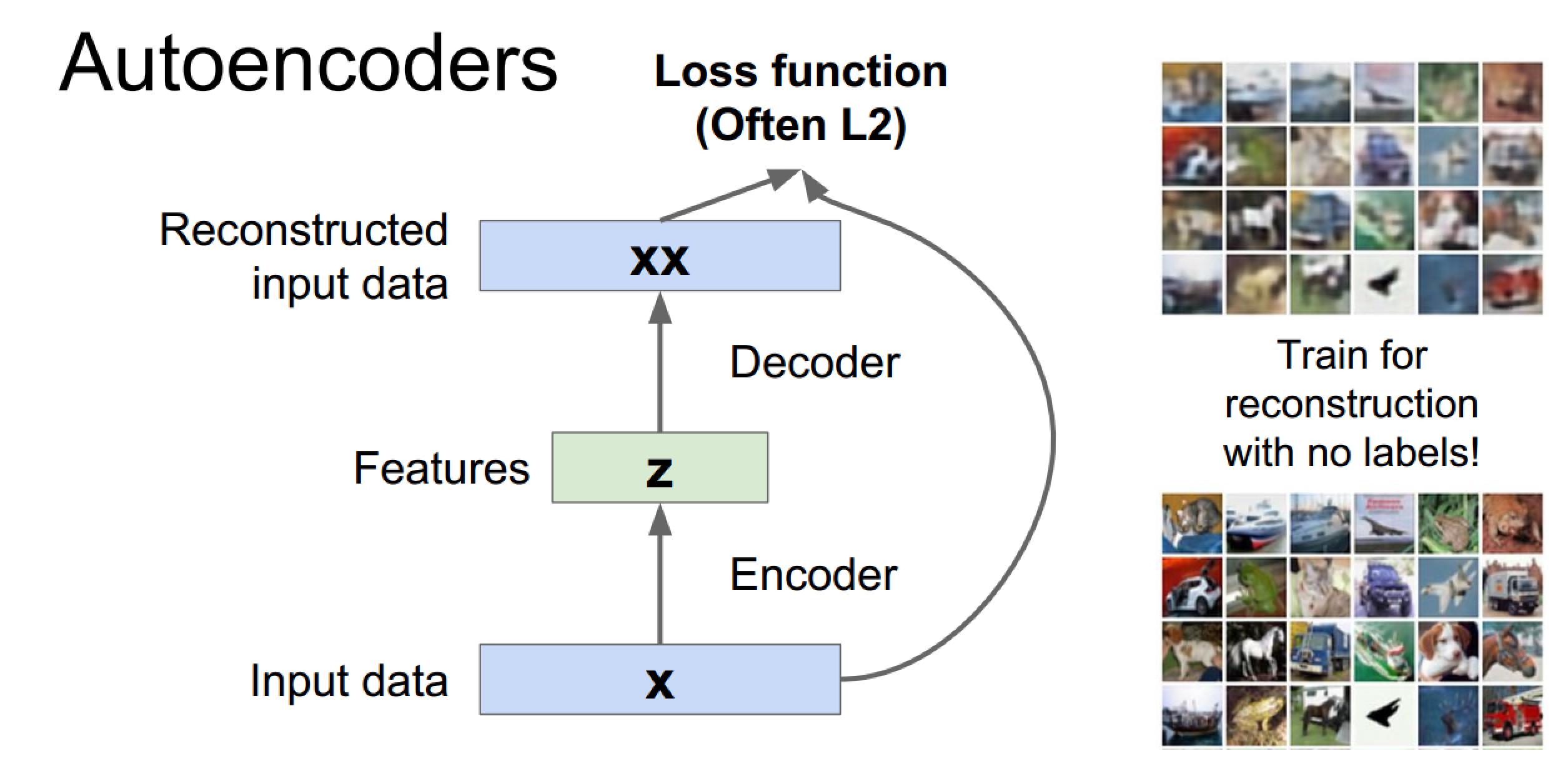
损失函数推荐L2

应用

由于重建已知数据是个没什么用的过程，所以自编码器一般在训练后会丢掉解码过程作为一个特征提取工具,

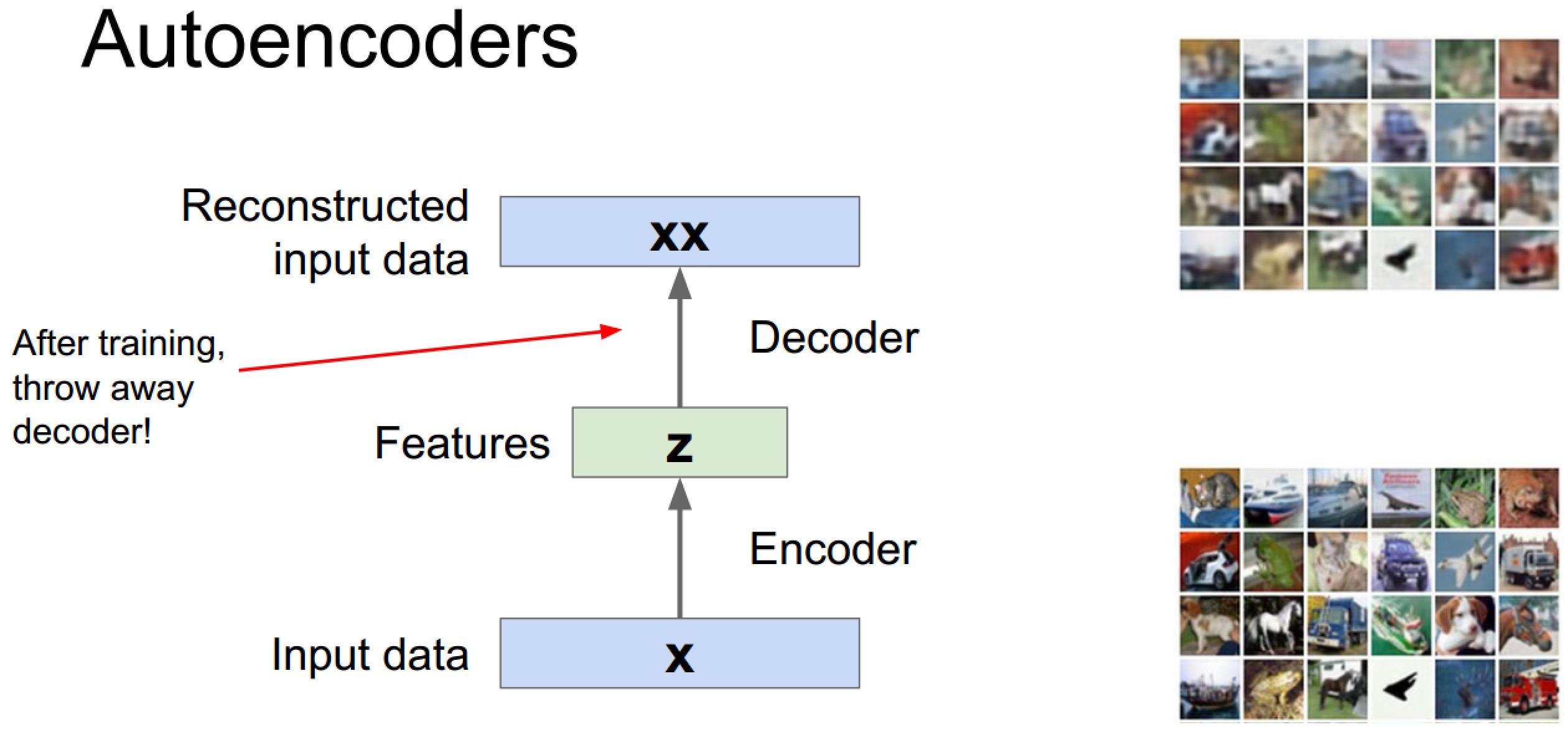
这里的思路是当我们有少量含标签数据以及大量无标签数据时，可以采用使用无标签数据训练自编码器，然后使用训练好的编码器加上分类器去提取有标签数据并训练分类器，不过现实可能不太好，这是老师的评价：

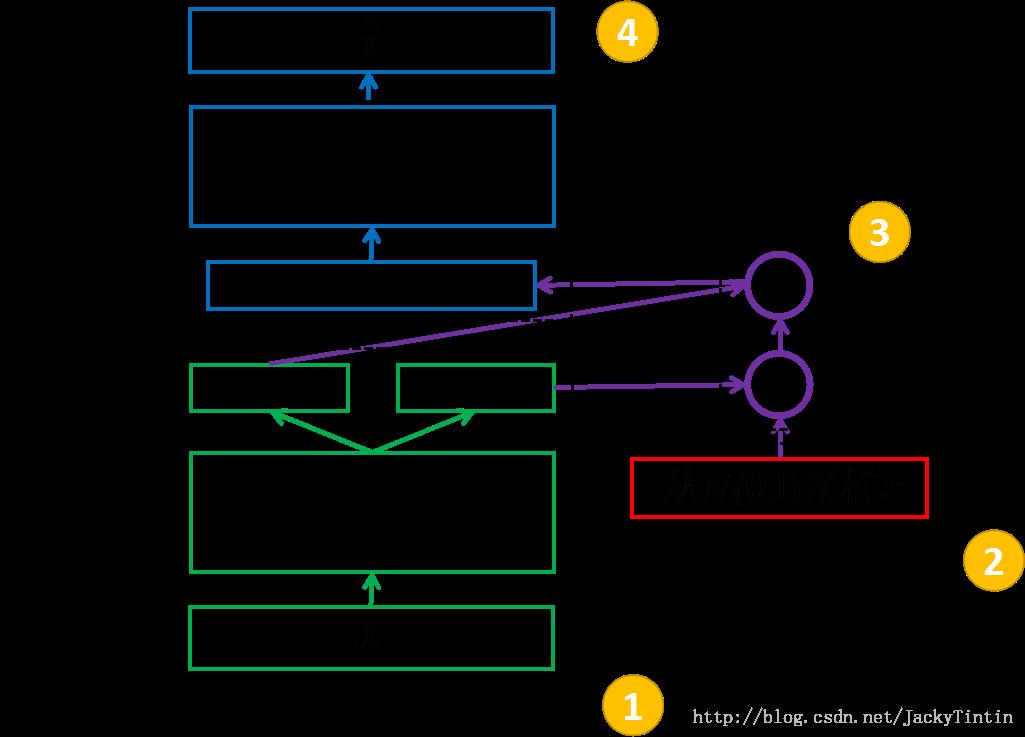
下图表示的是有标签数据经过训练好的编码器去训练分类器的过程，

 

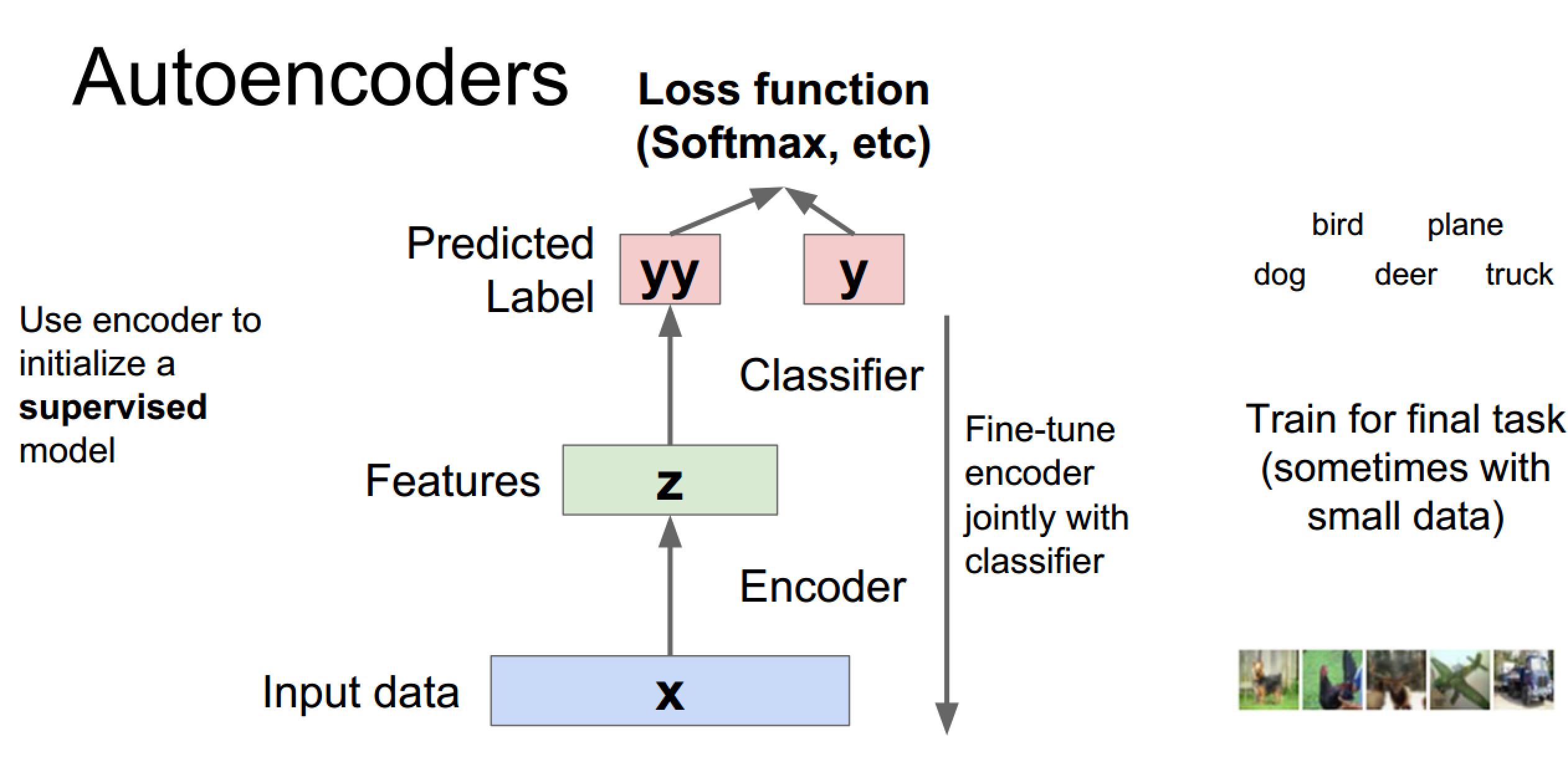
通过监督学习进行微调，也分两种，一个是只调整分类器（黑色部分）：

另一种：通过有标签样本，微调整个系统：（如果有足够多的数据，这个是最好的。end-to-end learning端对端学习）

一旦监督训练完成，这个网络就可以用来分类了。

在相关文献中有提到Greedy Training的，这是一种逐层训练的方式，是由于当时数据数量和计算能力决定的，现在已经不再使用了，老师说他特意提出来也只是为了防止大家看到这个词蒙圈。

 

Variational Autoencoder

TensorFlow实现

可以生成数据的自编码器变种——变分自编码器

位置一：我们将 encoder 的输出（2m个数）视作分别为m个高斯分布的均值（z_mean）和方差的对数（z_log_var），也就是特征z分布的描述

位置二、三：我们采样初始数据，根据 encoder 输出的均值与方差，生成服从相应高斯分布的随机数：

 eps = tf.random_normal((self.batch_size, n_z), 0, 1, 
                               dtype=tf.float32)
 # z = mu + sigma*epsilon
 self.z = tf.add(self.z_mean, 
                   tf.mul(tf.sqrt(tf.exp(self.z_log_sigma_sq)), eps))

 

 即使这样这里还有tips：

 

位置四：经由z还原x，计算loss，这里的loss计算颇为复杂，先给出结论，推导以后再说(逃... ...：

 

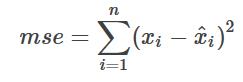
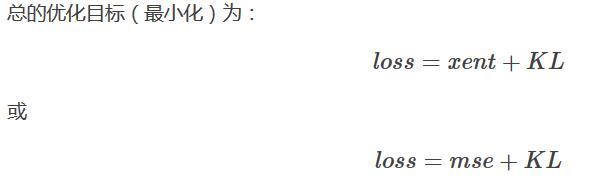
最后，尝试应用模型

下面是用于生成图片的应用，采样并尝试重构：

这里的z是直接采样得到的，而非先采样N(0,1)后使用均值标准差等还原出来的。

 

对抗式生成网络

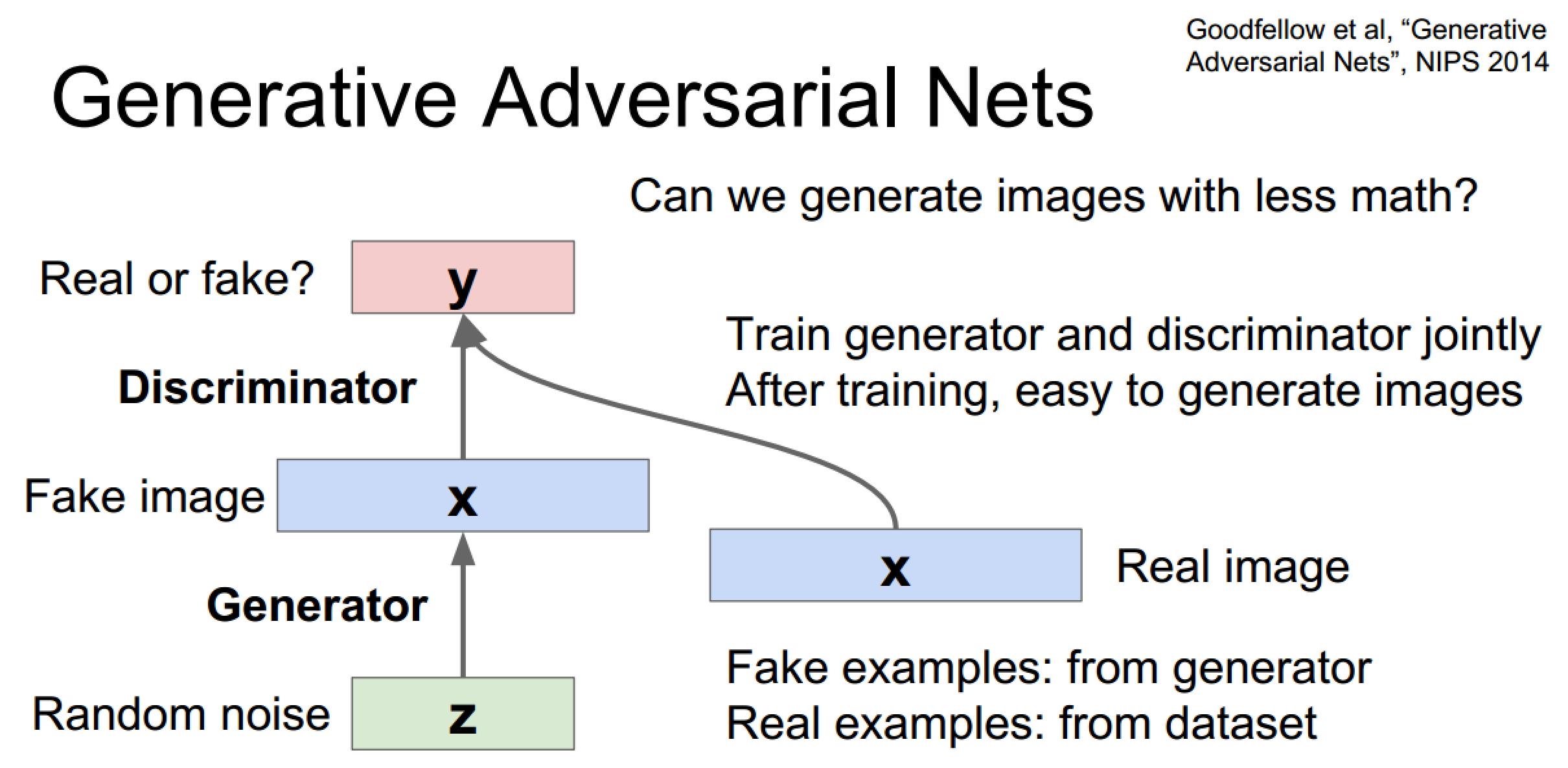
噪声->生成图 + 真图 ->分类器，实际属于二分类问题

由于结构简单在手写数字和人脸上效果不错，但对于复杂场景效果一般

 

提高思路一：多尺度生成

自右向左逐层生成图像

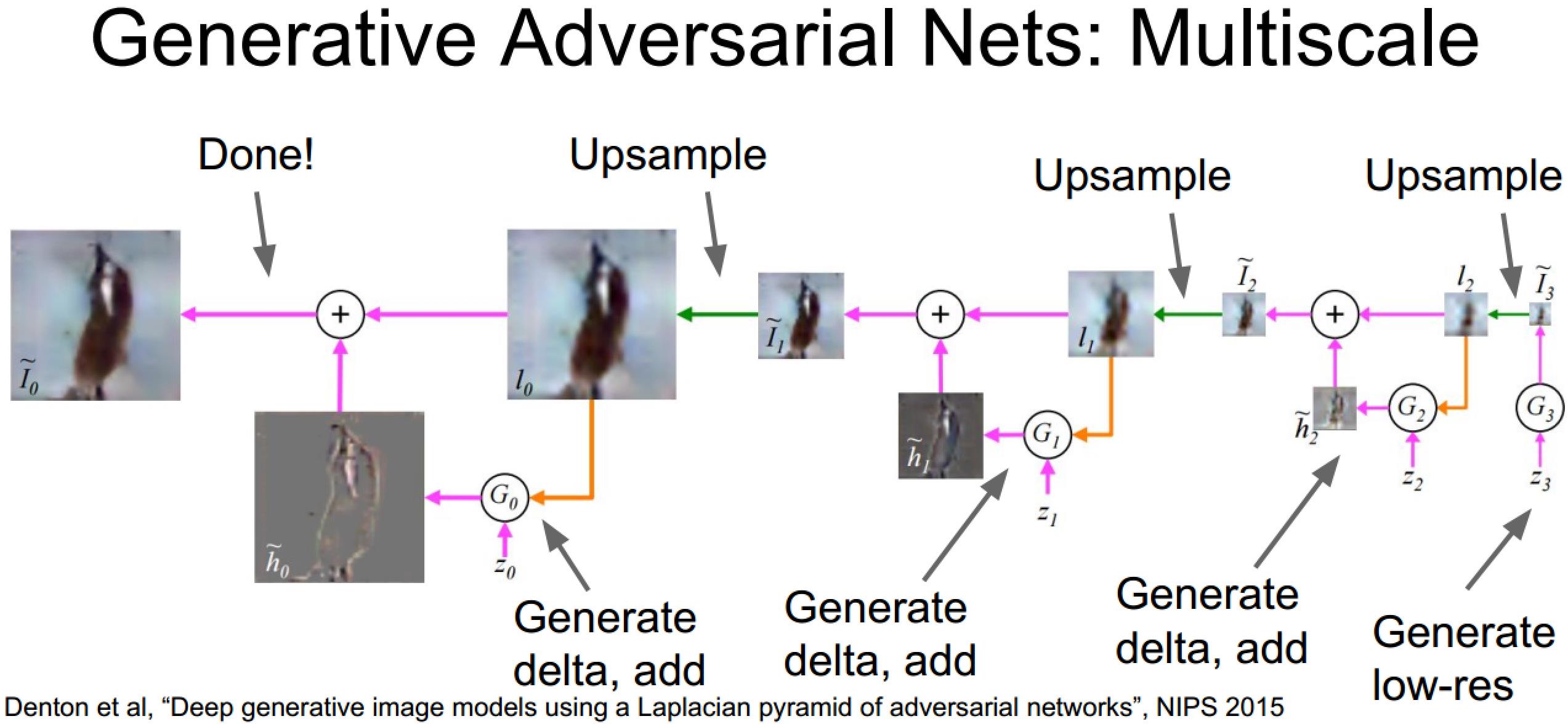
训练过程比较繁琐：每个尺度都要进行鉴别

 

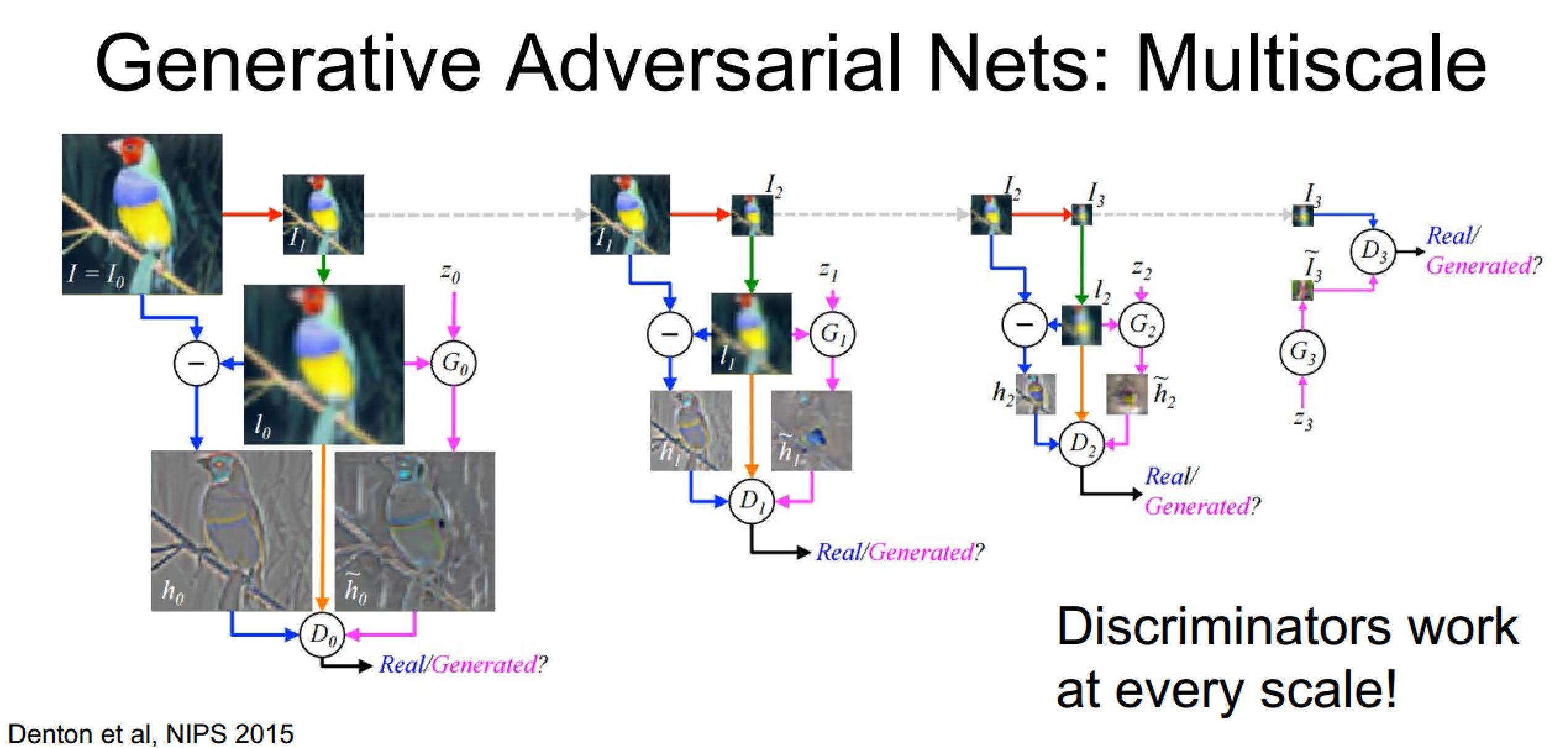
提高思路二：卷积生成网络

 

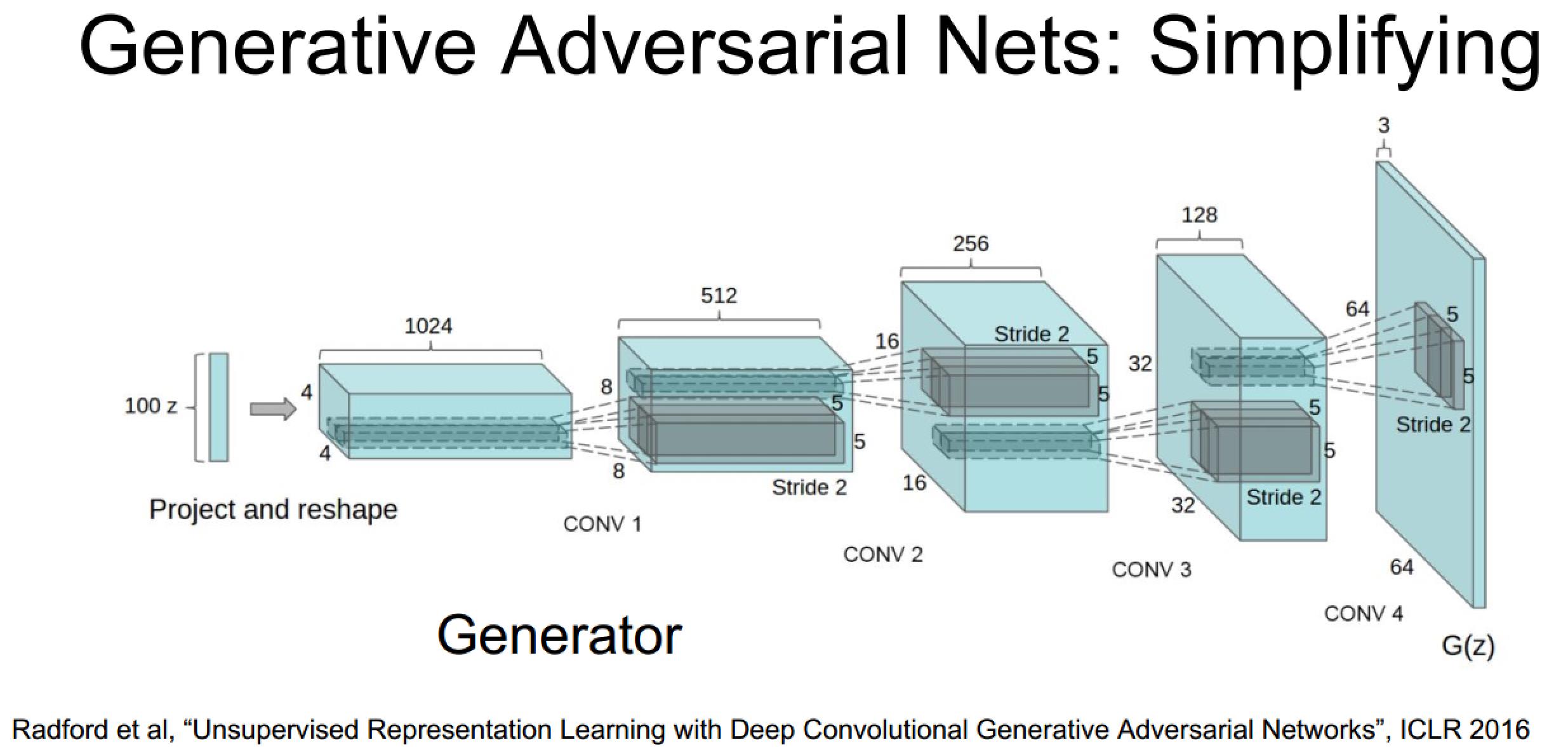
据说效果也很不错

 

混合型生成网络

 

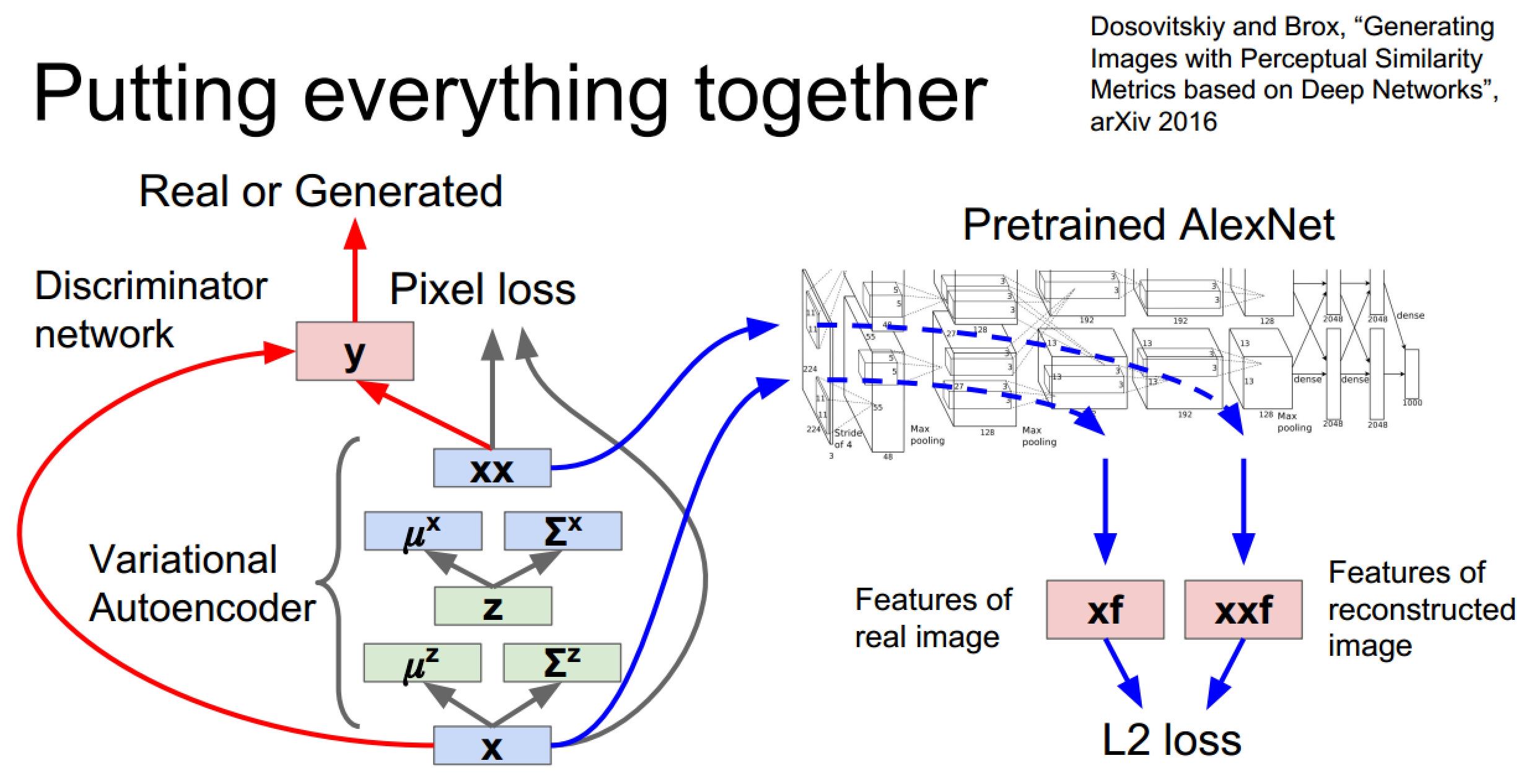
由于这部分内容不是课程重点，实际讲解也不够详细，所以记录的也就比较简洁了，主要把发展脉络理顺，各个PPT页上均有论文出处，如果有需要的话可以从论文入手。