Machine Learning - week 2 - Multivariate Linear Regression

Posted 2020-10-01

Multiple Features

上一章中，h_θ(x) = θ₀ + θ₁x，表示只有一个 feature。现在，有多个 features，所以 h_θ(x) = θ₀ + θ₁x₁ + θ₂x₂ + ... + θ_jx_j。
为了标记的方便，增加 x₀ = 1

用向量表示

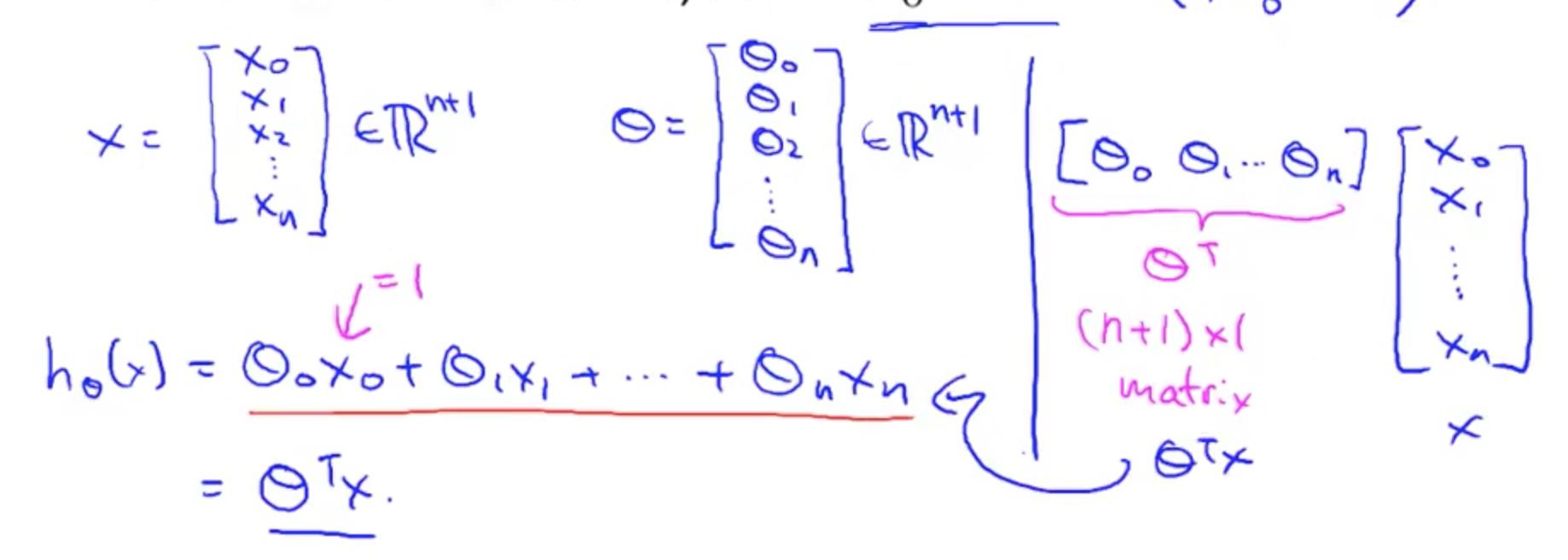
这里的 X 表示单行 Xⁱ。如果是表示所有的 h_θ(x)，就会 X * θ（X 表示所有 x 的值）

 

Gradient Descent For Multiple Features 也是同理，扩展到 j 个，就不再赘述。

Gradient Descent in Practice - Feature Scaling

逻辑是：确保所有的 features 在同一尺度。尺度理解为相差不超过 10 倍或者百倍。

Features 的范围越小，总的可能性就越小，计算速度就能加快。

 Dividing by the range

通过 feature/range 使每个 feature 大概在 [-1, 1] 的范围内

 下题是一个例子：

 

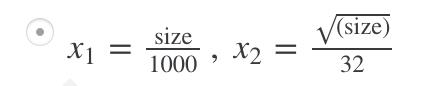
Mean normalization

将值变为接近 0。除了 x₀，因为 x₀ 的值为 1。

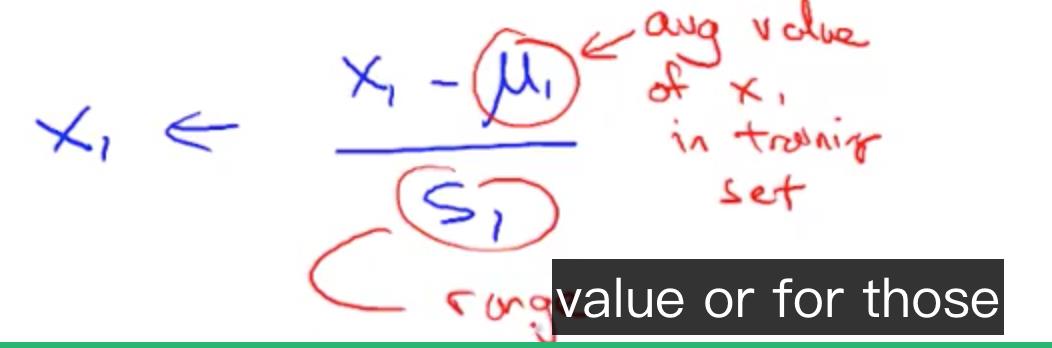
mu1 是 average value of x₁ in trainning sets;

S₁ 是 x₁ 的范围大小，比如卧室是 [0, 5]，那么范围为 5 - 0 = 5。也可以设置成标准差（在练习中就是这个）

需要将 x0 排除。

 

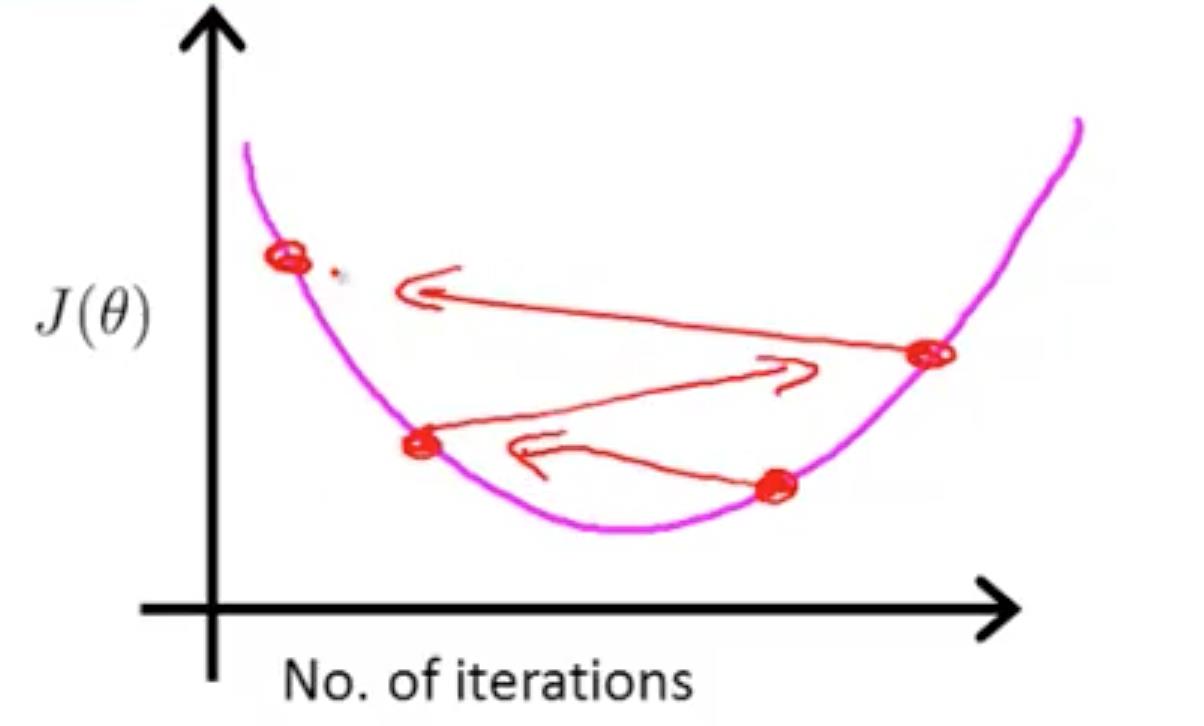
确保 gradient descent 工作正确

如上图，这个图像是正确的，随着循环次数的增加，J(θ) 主键减小。超过一定循环次数之后，J(θ) 曲线趋于平缓。可以根据图像得出什么时候停止，或者当每次循环，J(θ) 的变化小于 ε 时停止。

 

图像上升

说明 α 取值大了，应该减小。上图的图像另一种观看方式：

如果 α 足够小，那么能缓慢但完全覆盖。

如果 α 太大：在每次循环时，可能不会减少从而不能完全覆盖。

可以由程序来自动选择，后面会提到。

Features and polynomial regression

可以使用自定义的 features 而不是完全照搬已存在的 features。比如房子有长宽两个属性，我们可以创建一个新属性--面积。然后，表达式变成

，但是这个曲线是先减小后增大的，与实际数据不符（面积越大，总价越高）。所以调整为

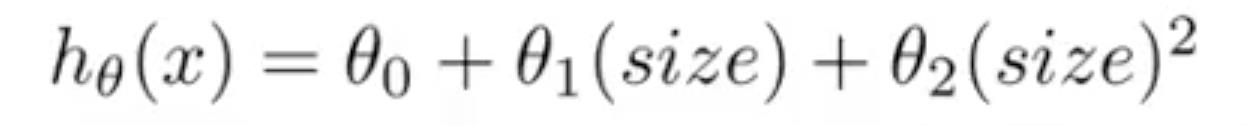（可以调整表达式直到符合数据为止）。

Normal equation

Gradient Descent 随着循环次数增加，逐步逼近最小值。如图：

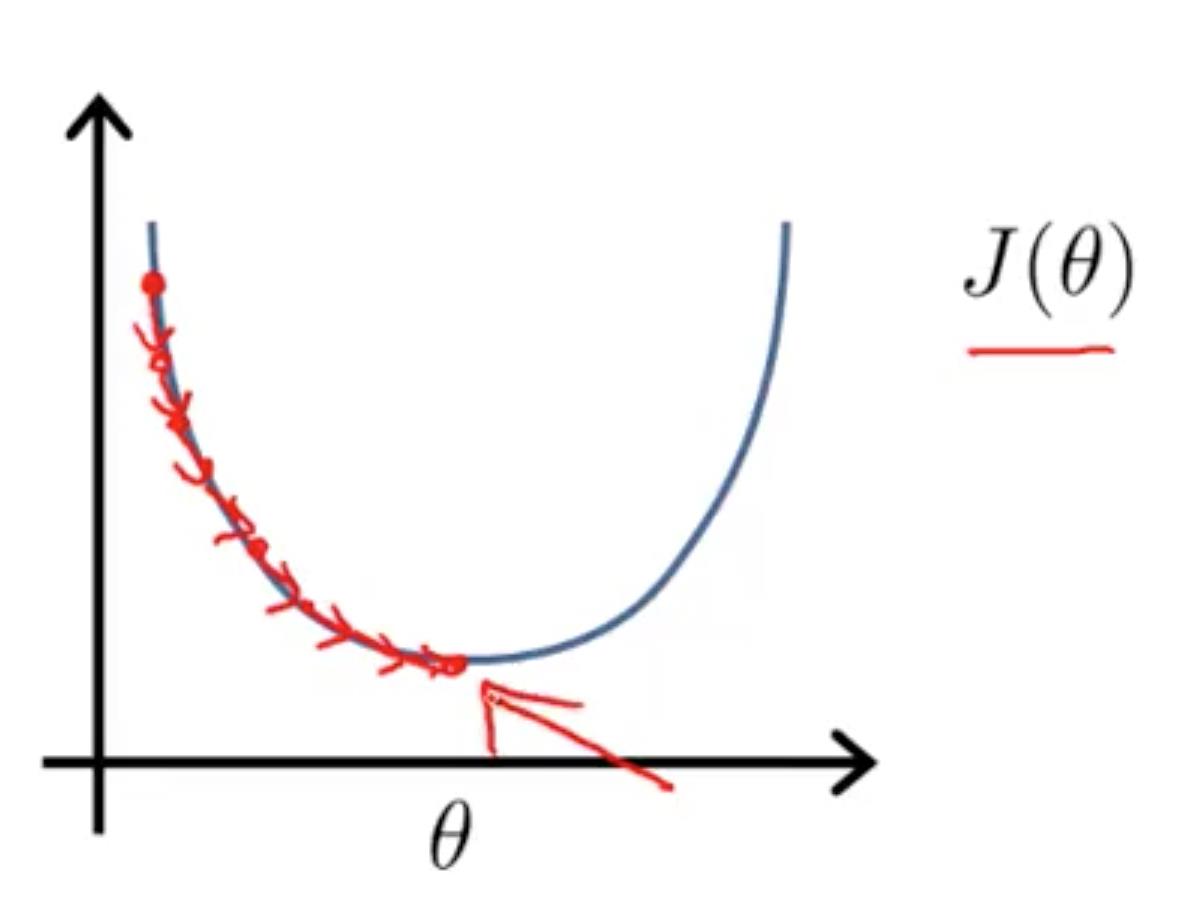
Normal equation 是通过方法直接计算出 θ。

 

导数为 0 时最小

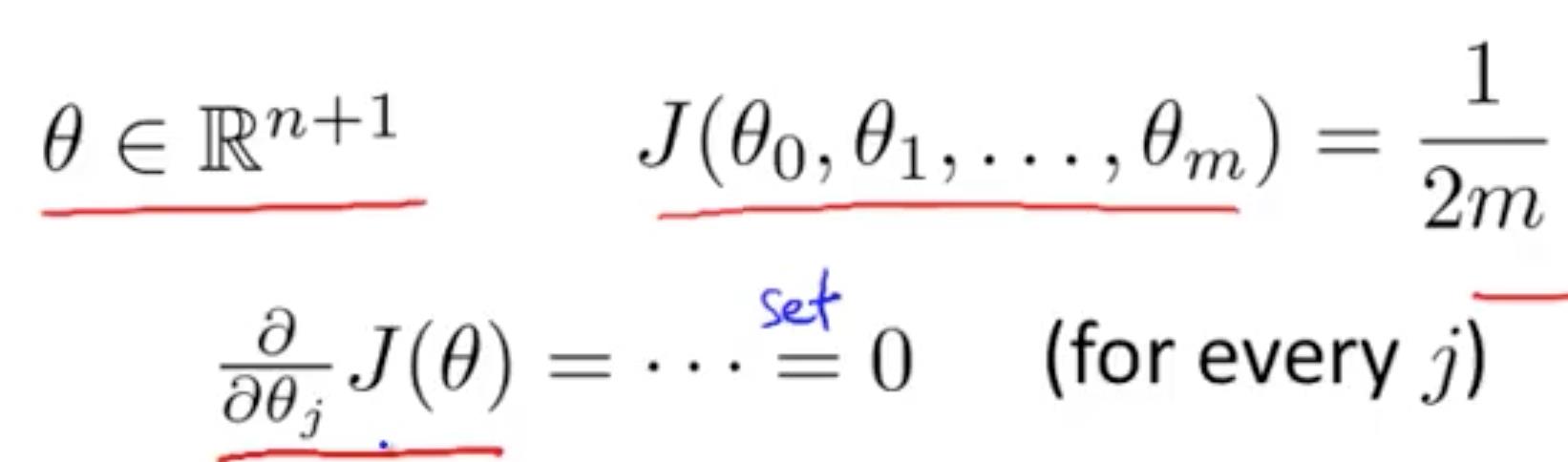
然后解出 θ₀ 到 θ_n

求解 θ 的方程

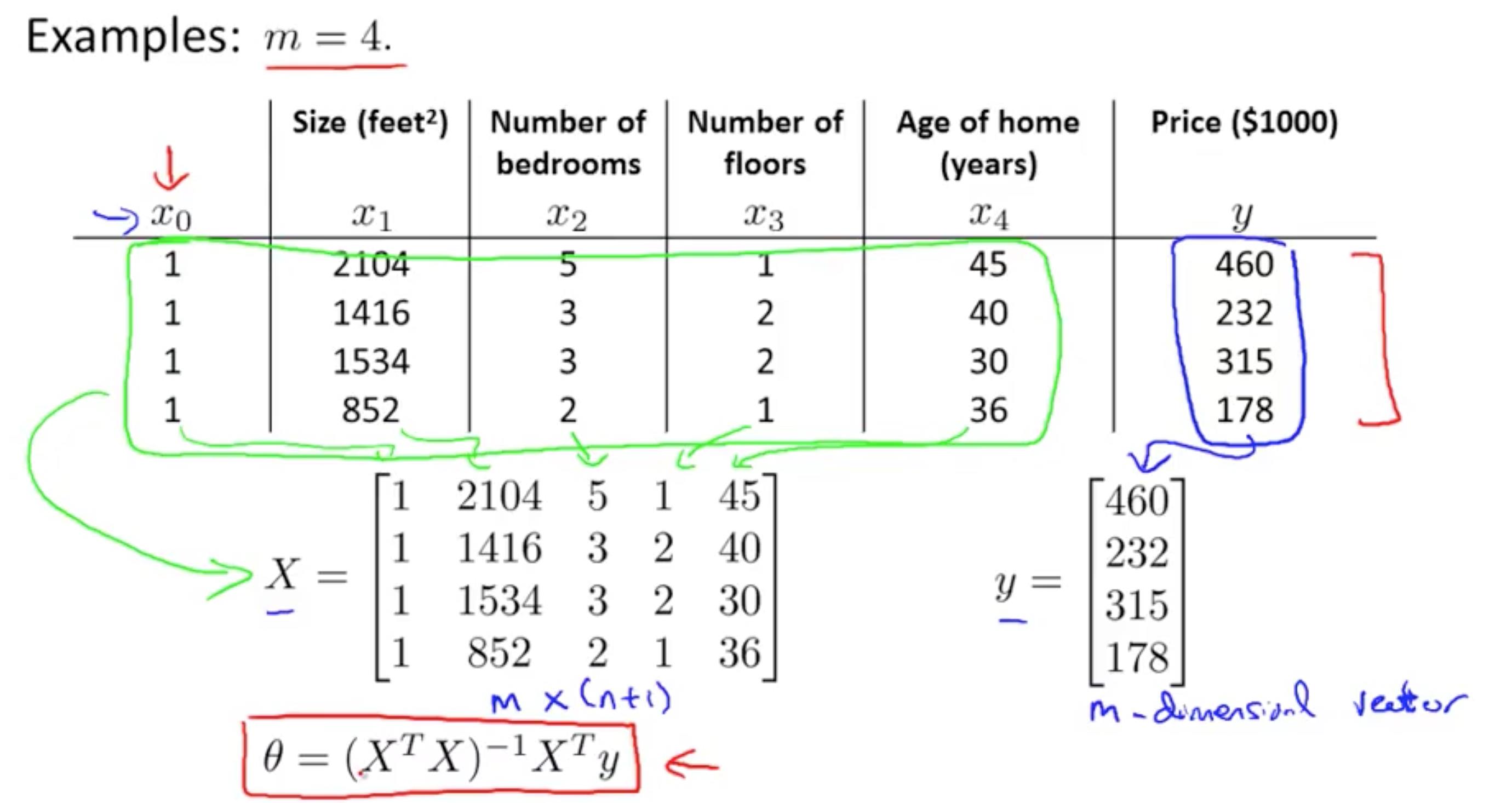
Matrix 概念见 Machine Learning - week 1

什么时候用 Gradient Descent 或者 Normal Equation

当 n 较大时，右边的会很慢，因为计算  是 O(n³)

当 n 小的时候，右边会更快，因为它是直接得出结果，不需要 iterations 或者 feature scaling。

 

如果  是 non-invertible？

1. Redundant features (are not linearly independent).

E.g. x₁ = size in feet²; x₂ = size in m²

2. Too many features(e.g. m <= n)

比如 m = 10, n = 100，意思是你只有 10 个数据，但有 100 个 features，显然，数据不足以覆盖所有的 features。

可以删除一些 features（只保留与数据相关的 features）或者使用 regularization。

 

习题

1. 

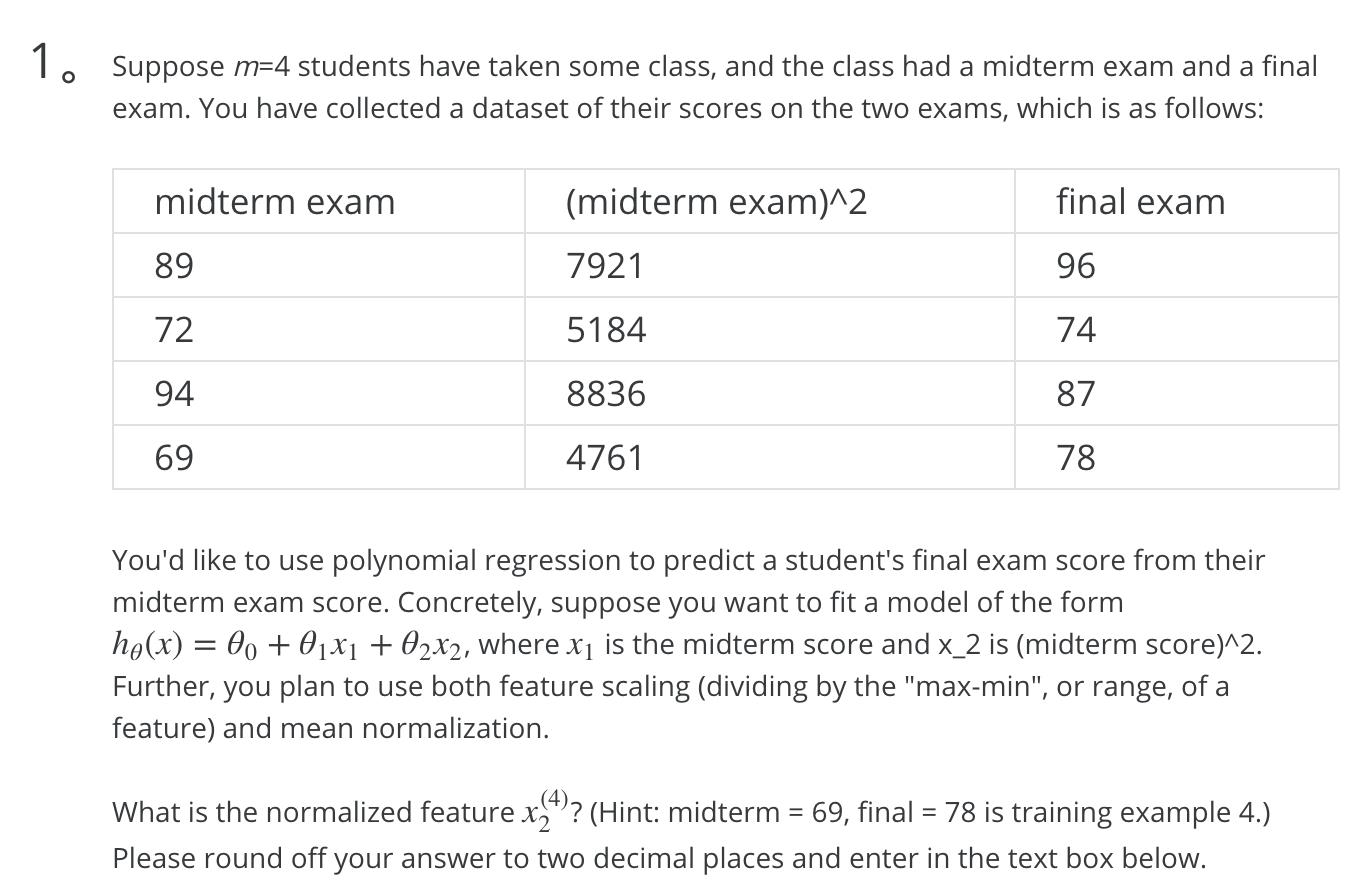
不知道如何同时使用两种方法，这两种方法是否是顺序相关的？

使用 Dividing by the range

range = max - min = 8836 - 4761 = 4075

vector / range 后变为 

1.9438
1.2721
2.1683
1.1683

对上述使用 mean normalization

avg = 1.6382

range =  2.1683 - 1.1683 = 1

x2(4) = (1.1683 - 1.6382) / 1 = -0.46990 保留两位小数为 -0.47

 

5. 

上面提到了“Features 的范围越小，总的可能性就越小，计算速度就能加快。”（多选题也可以单选）

Octave Tutorial

介绍了 Octave 的常用语法。

Vectorization

使用 vectorization 会比 for loop 更加高效。

例子

更复杂的例子

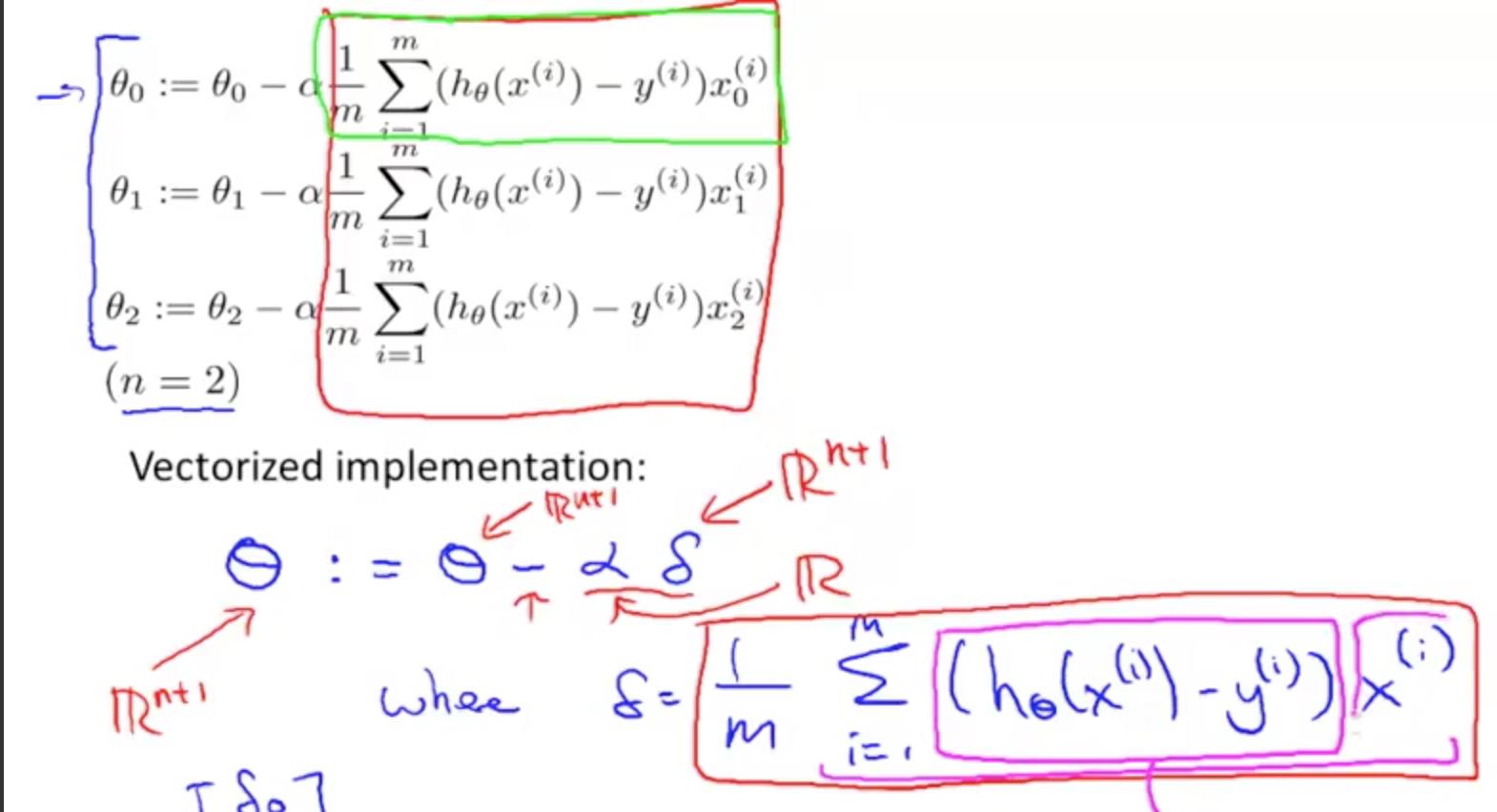
怎样把 delta vectorized 还没有理解。整体思想了解了。

 

Octave arithmetic operators 有一些不符合你的直觉。

比如 ^ 与 .^

X =

 

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

 

octave:80> X .^ 2

ans =

 

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

   1   1   1   1   1   1   1

 

octave:81> X ^ 2

ans =

 

   7   7   7   7   7   7   7

   7   7   7   7   7   7   7

   7   7   7   7   7   7   7

   7   7   7   7   7   7   7

   7   7   7   7   7   7   7

   7   7   7   7   7   7   7

   7   7   7   7   7   7   7