Machine Learning - week 3
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Machine Learning - week 3相关的知识,希望对你有一定的参考价值。
Classification
使用线性回归来分类,会很不准确。并且,它的范围也会超出 {0, 1}。所以使用下面的逻辑回归模型。
Hypothesis representation
线性回归中 hθ(x) = θTx,而在逻辑回归中,我们想要 hθ(x) ∈ [0, 1]。对结果进行双曲化处理:
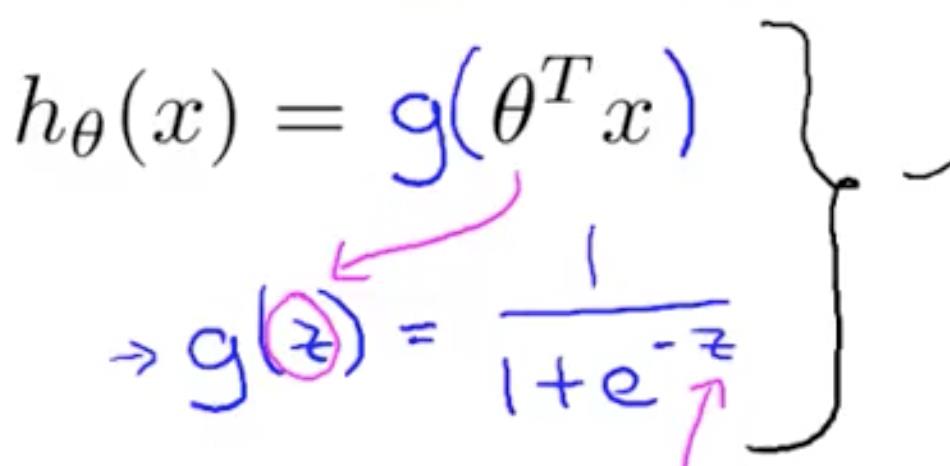
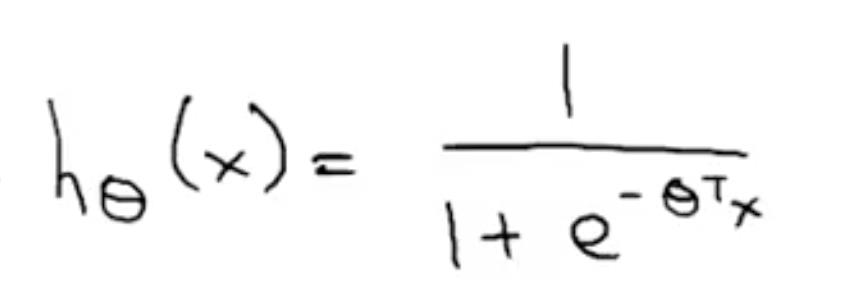
,图象如右图: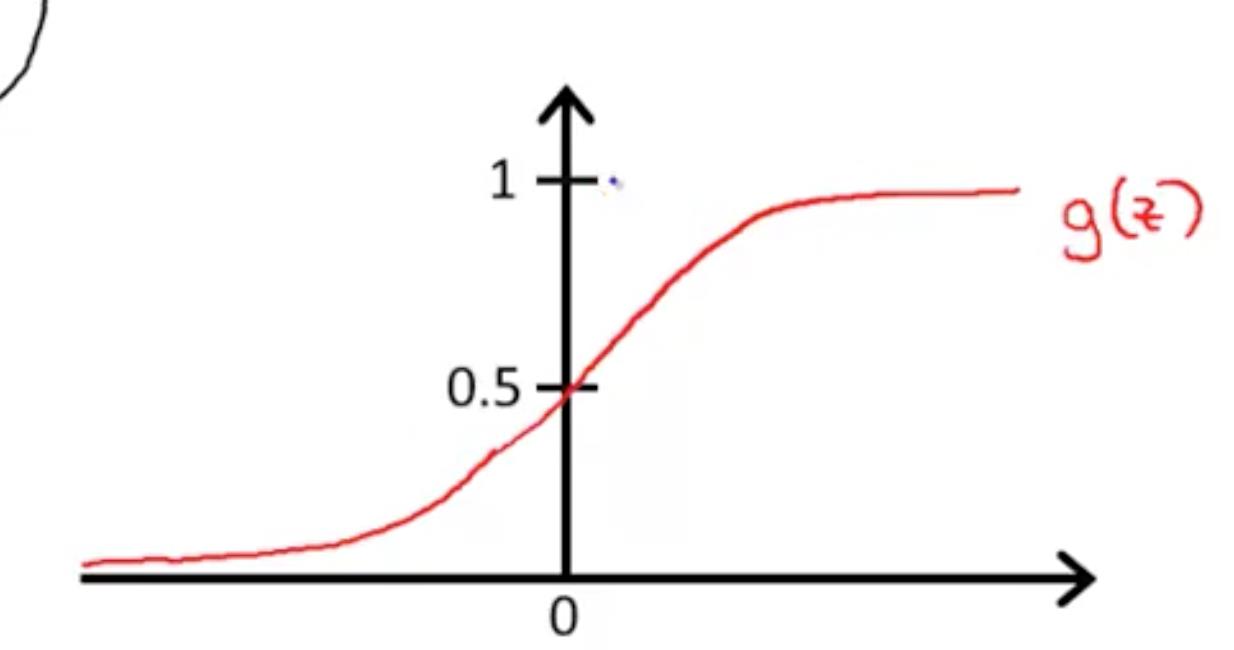 ,范围是 (0, 1)。
,范围是 (0, 1)。
在线性回归中,hθ(x) 就表示 y 的值。在逻辑回归中,表示『基于输入的 x,y=1 的概率是多少』。用数学形式表示: 。
。
Desicion boundary
逻辑回归中, hθ(x) 是属于 (0, 1) 范围内的连续的值。但我们的分类结果只有 0 或者 1,所以就需要一个决策边界。这里,取平均值, y = 0.5。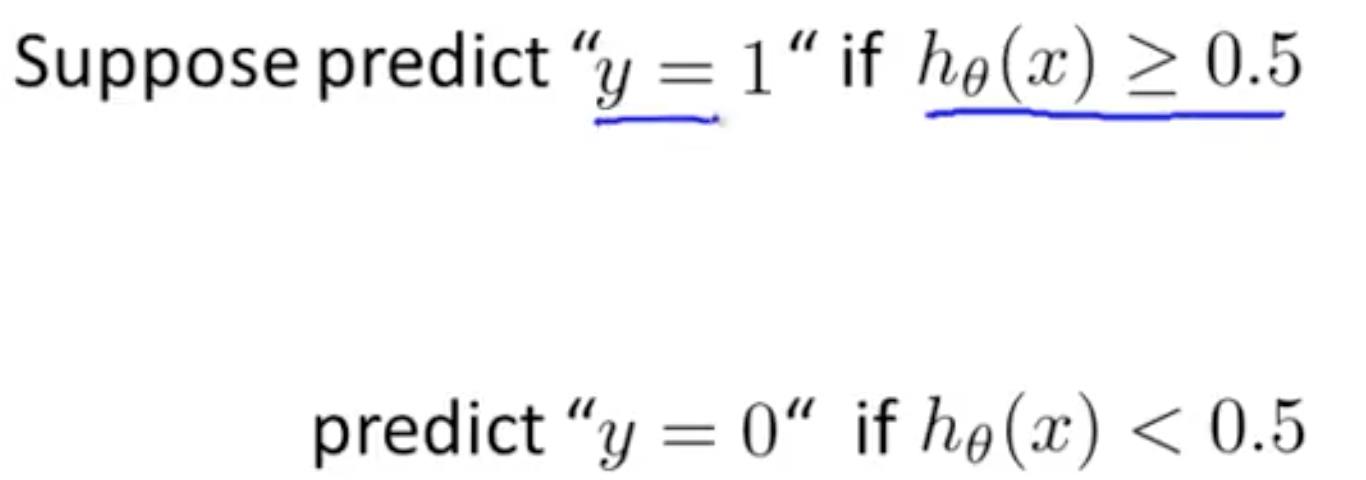 。从上方的双曲线图中可以看出,当 z > 0,y=1,即 θTx >= 0 时,hθ(x) >= 0.5。将区域分为 y=0 和 y=1 的两个区域。
。从上方的双曲线图中可以看出,当 z > 0,y=1,即 θTx >= 0 时,hθ(x) >= 0.5。将区域分为 y=0 和 y=1 的两个区域。
决策边界是针对与 θ 的属性,所以 θ 不同,决策边界也不同。
非线性的决策边界
当 hθ(x) 是多项式的时候,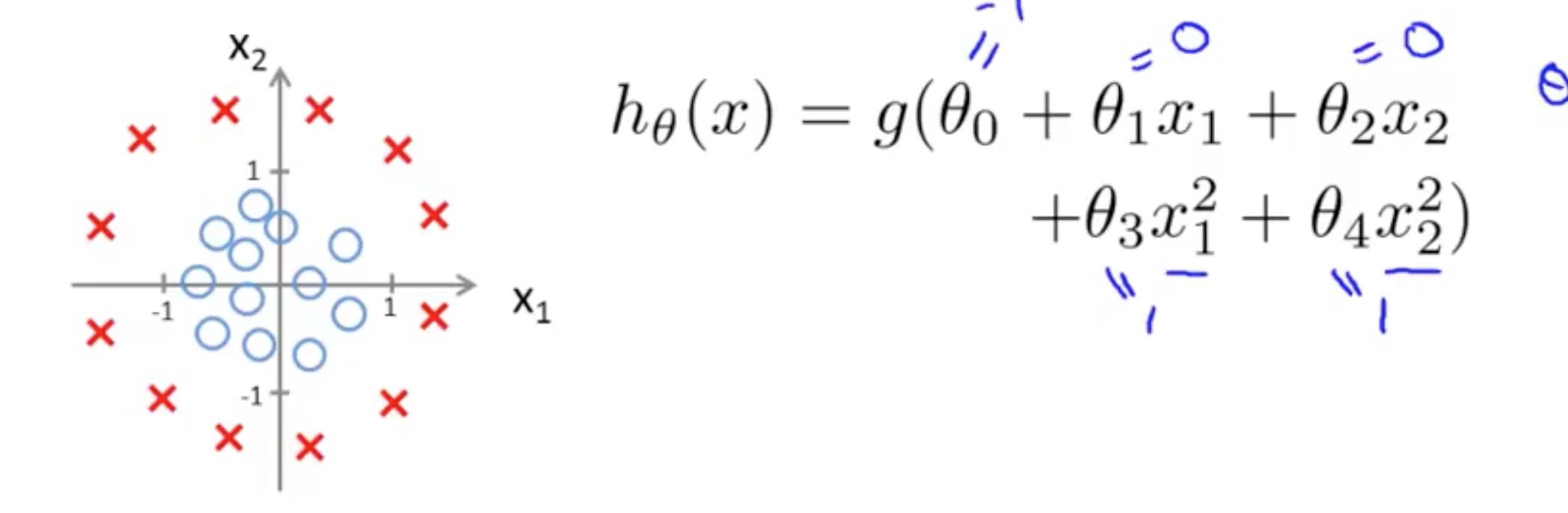 。
。
当多项式更加复杂的时候,决策边界的形状也会更加复杂。
Cost Function

当 y = 1 时,如果 hθ(x) = 0,那么 cost 接近无限大。因为你预测不是恶性肿瘤,但实际上是恶性肿瘤。同样,如果不是恶性肿瘤,你预测 y = 1 的概率越接近 1,那么误差越小。
y = 0 时的情况同理可得。
化简的 Cost Function 和 Gradient Descent
化简后(通过遍历所有情况能够证明)
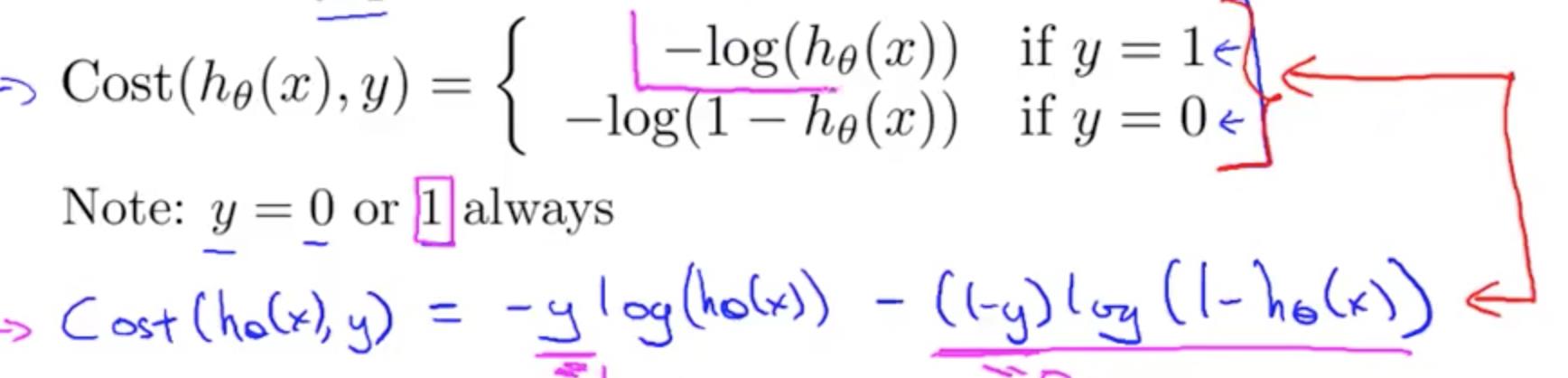
J(θ) 为
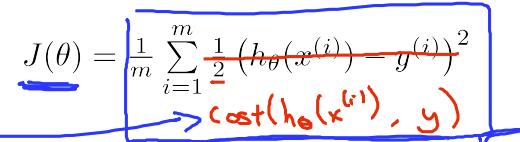
Gradient Descent

Logistic Regression 与 Linear Regression 在 Gradient Descent 上的不同,就是 hθ(x) 的不同。
用矩阵计算为:
grad = (X\' * (h - y)) / m;
这里是求和,所以最终是 1*1,所以转置成这样的形式 [1 * n] * [n * 1]。
Advanced Optimization
使用更高级的算法,不需要手动选择 learning rate;通常比 gradient descent 更快;缺点是更复杂。
可以使用库直接调用这些算法,不需要深入理解它们。

% 我们传入了 GradObj,最大循环次数为 100 次
octave:1> options = optimset(\'GradObj\', \'on\', \'MaxIter\', \'100\')
options =
scalar structure containing the fields:
GradObj = on
MaxIter = 100
octave:2> initialTheta = zeros(2,1 )
initialTheta =
0
0
jVal 表示 j(θ) 的计算方法
gradient 表示对应 θ 的计算方法(求导)
Multiclass Classfication
大于 2 个类别,如邮件分类:工作、朋友、家庭。
使用 one-vs-rest 方法。
假设有 3 类,我们将测试数据分为 C32 类别,把一类看作 positive,其他类看做 negative。这样我们就能得到三个 h(θ)
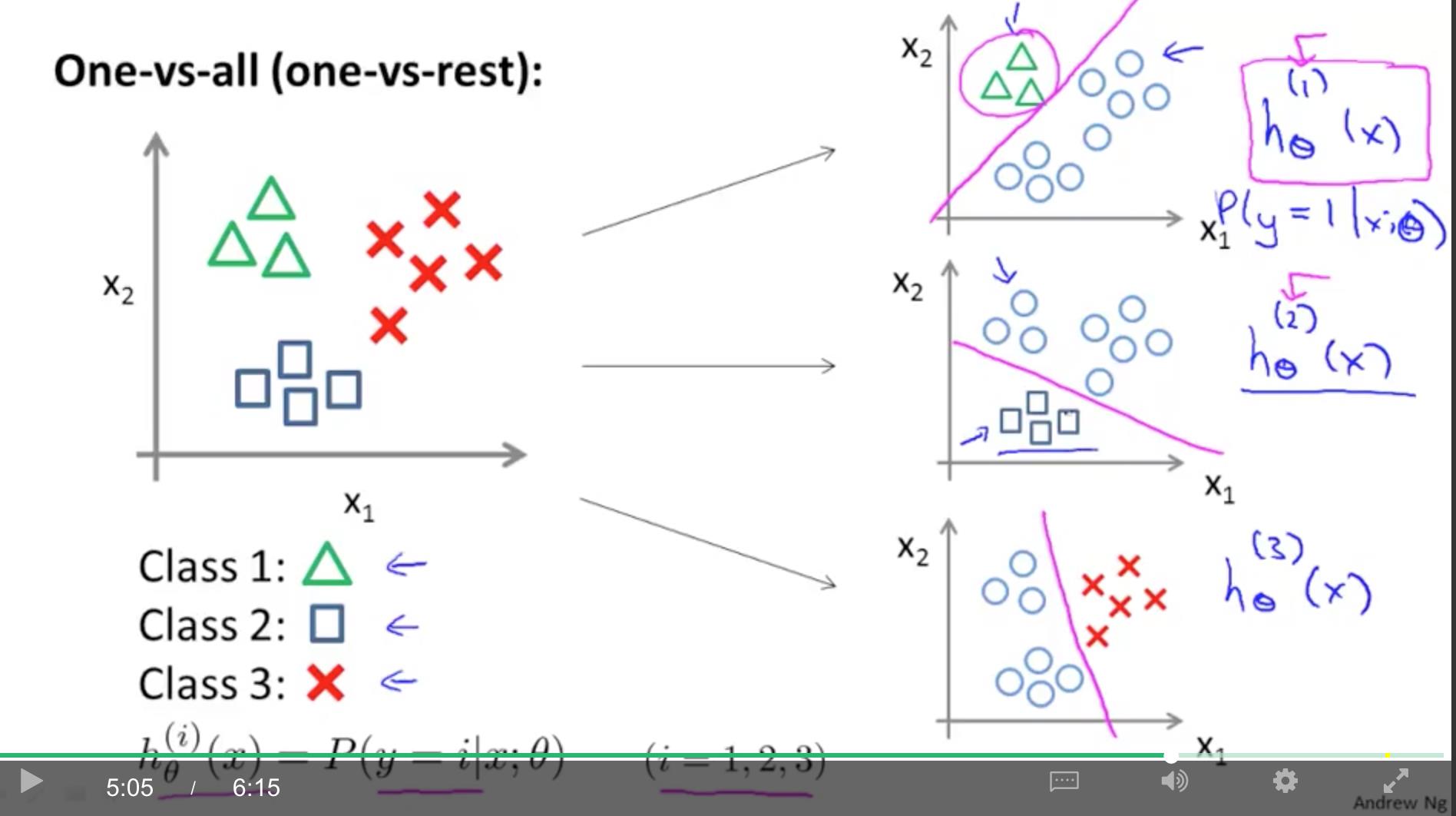
在预测时,由于有三个 h(θ) 函数,所以有三个结果。一般是取概率最大的作为最终预测结果。
习题
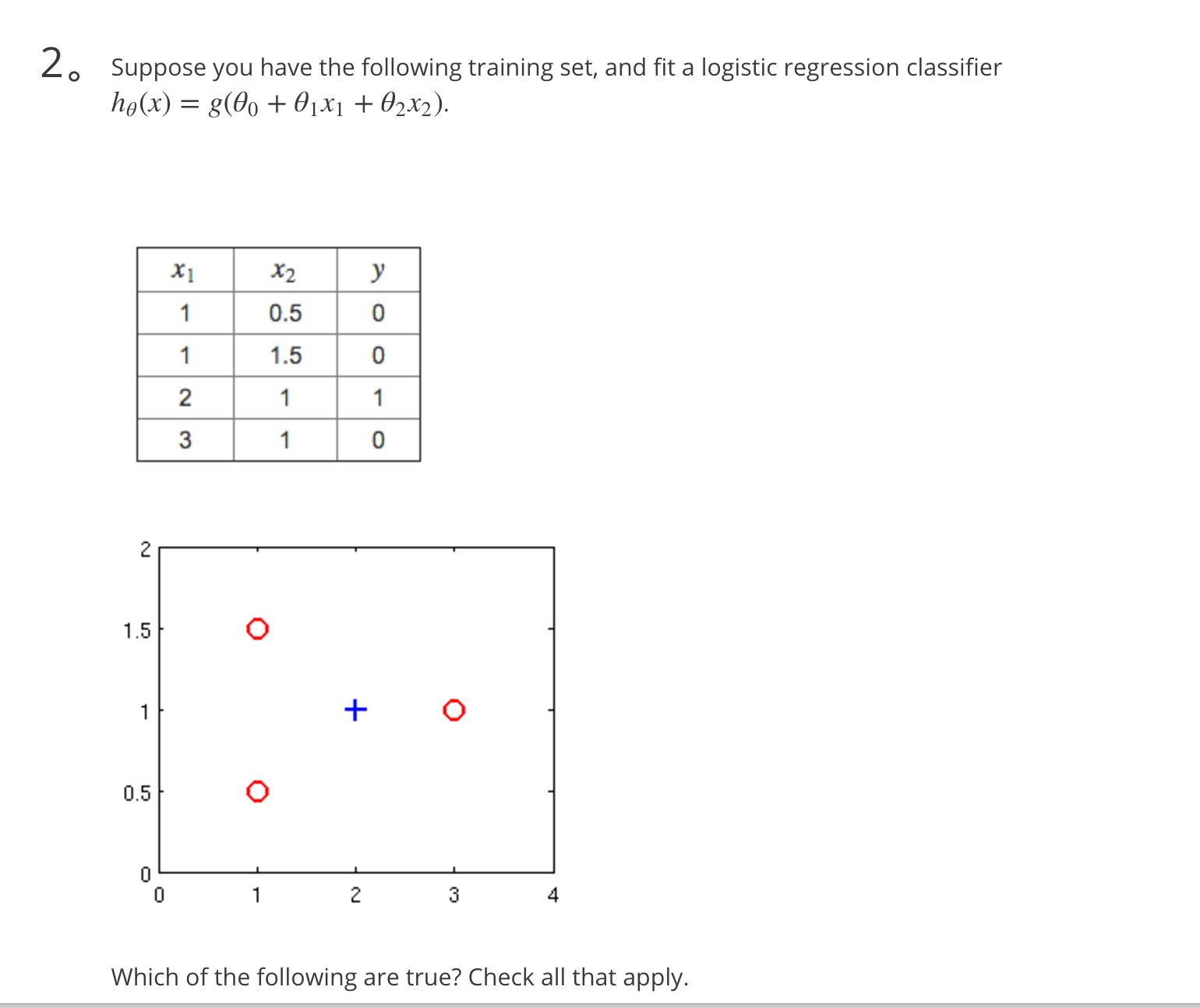

从图中可以可以看出,应该是一个圆把蓝色的圈住,所以应该有两个 x2
1. 如何判断是否 convex,gradient 什么情况下(能/否) converge
-
- 判断 convex 要由数学证明完成,我们是选择别人证明好的 cost function,这里不做证明。
-
- 确保 learning rate α 被设置合适。
2. 增加多项式 features 可以增加对训练数据的匹配。更匹配的意思是:使曲线与数据更贴近。
对。
3. 能否被直线分割为两段有什么区别?对 converge 有影响吗?
不知道。应该没有
non-linear decision boundaries

4. linear regression 与 logistic regeress 的区别?两者会相同吗?在什么情况下会相同?
Gradient Descent 的公式是一样的,但是 hθ(x) 不一样

为什么 hθ(x) 要不一样呢?
想要 0 < hθ(x) < 1,所以定义了 Logistic function (sigmoid function)。
还是有错误。

有错误
第二个选项:应该对的。J(θ) 表示的是误差。
第三个选项:没有理解清楚。算错误的
第四个选项:

没有提到 local minimum,但我认为有这个原因。
如何用 vector 表示 J(θ)
3. 
从课件中查到公式为 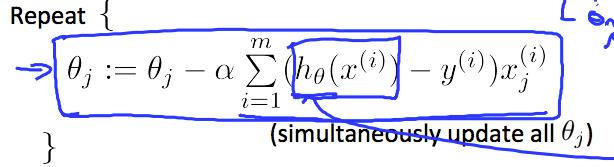 ,所以 3、4 是对的。
,所以 3、4 是对的。
1 是错误的。
θTx - y(i) 为 n * 1 的 vector。乘以 x 第 i 行。应该是乘以 x 第 i 行第 j 个,其中 j 是不变的。所以是错误。

第一个,对的
第二个,意思是:允许你对于每个 y 来自固定的、离散的几组值。对的。
第三个,对。范围就是 >= 0 不会变
第四个,对
存在错误。
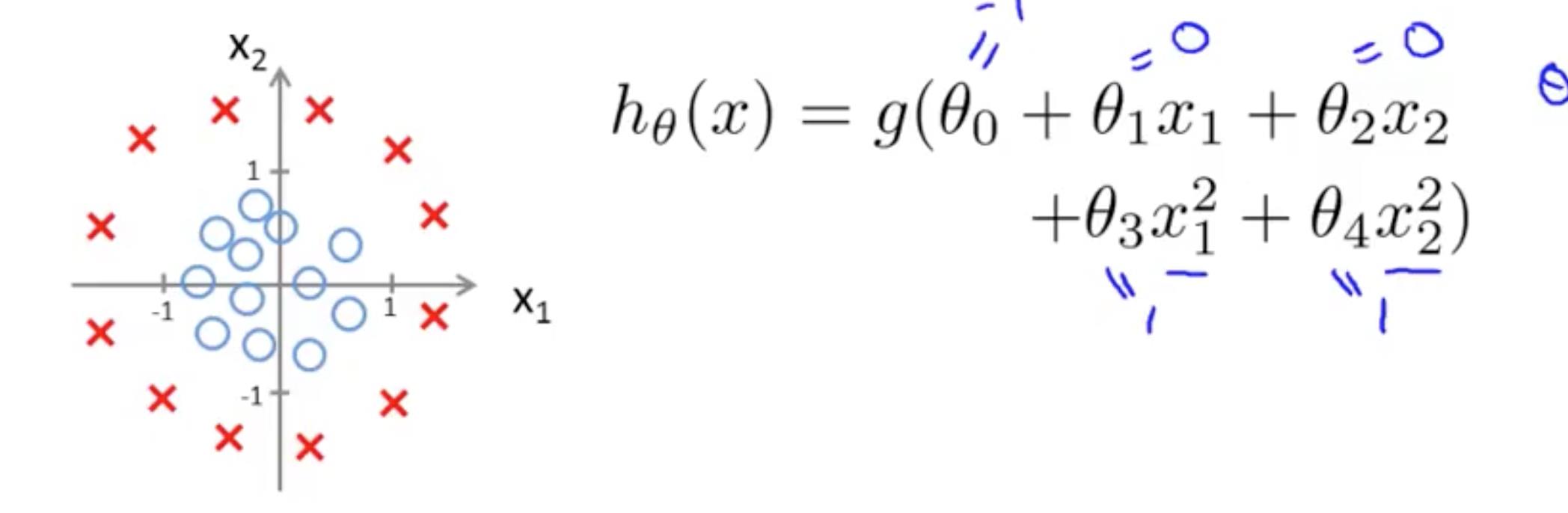
以上是关于Machine Learning - week 3的主要内容,如果未能解决你的问题,请参考以下文章
Machine Learning Week 3-advanced-optimization
Machine Learning - week 2 - 编程
Machine Learning - week 4 - 习题