Machine Learning - week 2 - 编程

Posted 2020-10-02

 

3. % J = COMPUTECOST(X, y, theta) computes the cost of using theta as the

% parameter for linear regression to fit the data points in X and y

 

传入的参数的 size 

size(X)

ans =

 

   m    n

 

octave:4> size(y)

ans =

 

   m    1

 

octave:5> size(theta)

ans =

 

   n   1

 

根据公式 

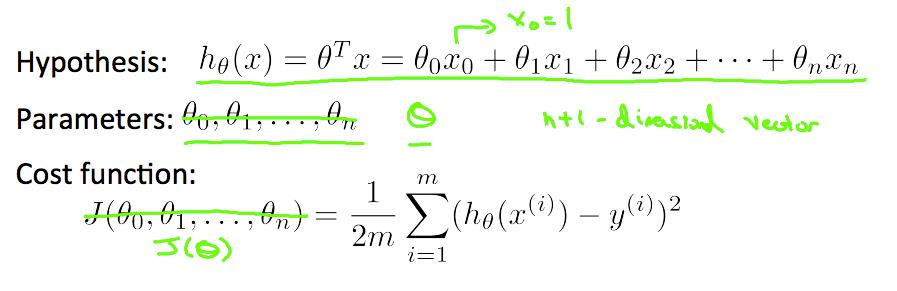
h_θ(x) = X * theta，size 为 m * 1。然后与 y 相减，再对所有元素取平方，之后求和。具体代码如下

function J = computeCost(X, y, theta)

% Initialize some useful values
m = length(y); % number of training examples

J = 0;

h = X * theta
J = 1/(2*m) * sum( (h - y) .^ 2 )

end

gradientDescent　　

 

i 表示的行数，j 表示的是列数。每列表示一个 feature。x_j⁽ⁱ⁾ 表示第 j 列第 i 个。如何用向量表示这个乘法？

首先，弄清楚 的意思。（对于每行 x 与对应的 y）预期值与真实值的差值 * 对应行的 x 的第 j 列个。j 与 θ 是对应的。下面是代码

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)

m = length(y); % number of training examples
n = columns(X);
J_history = zeros(num_iters, 1);

for iter = 1:num_iters

    h = X * theta;

    for j = 1:n
        % 差值点乘    
        delta = alpha/m * sum(  (h - y) .* X(:, j));
        theta(j) = theta(j) - delta;
    end

    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);

end

end
　　

　点乘，对应元素相乘

[1; 2; 3] .* [2; 2; 2]
ans =

   2
   4
   6

 先弄清楚公式的意思，再寻找 Octave 中的表示方法。　　

 

等高线图怎么看

这是练习脚本生成的等高线。

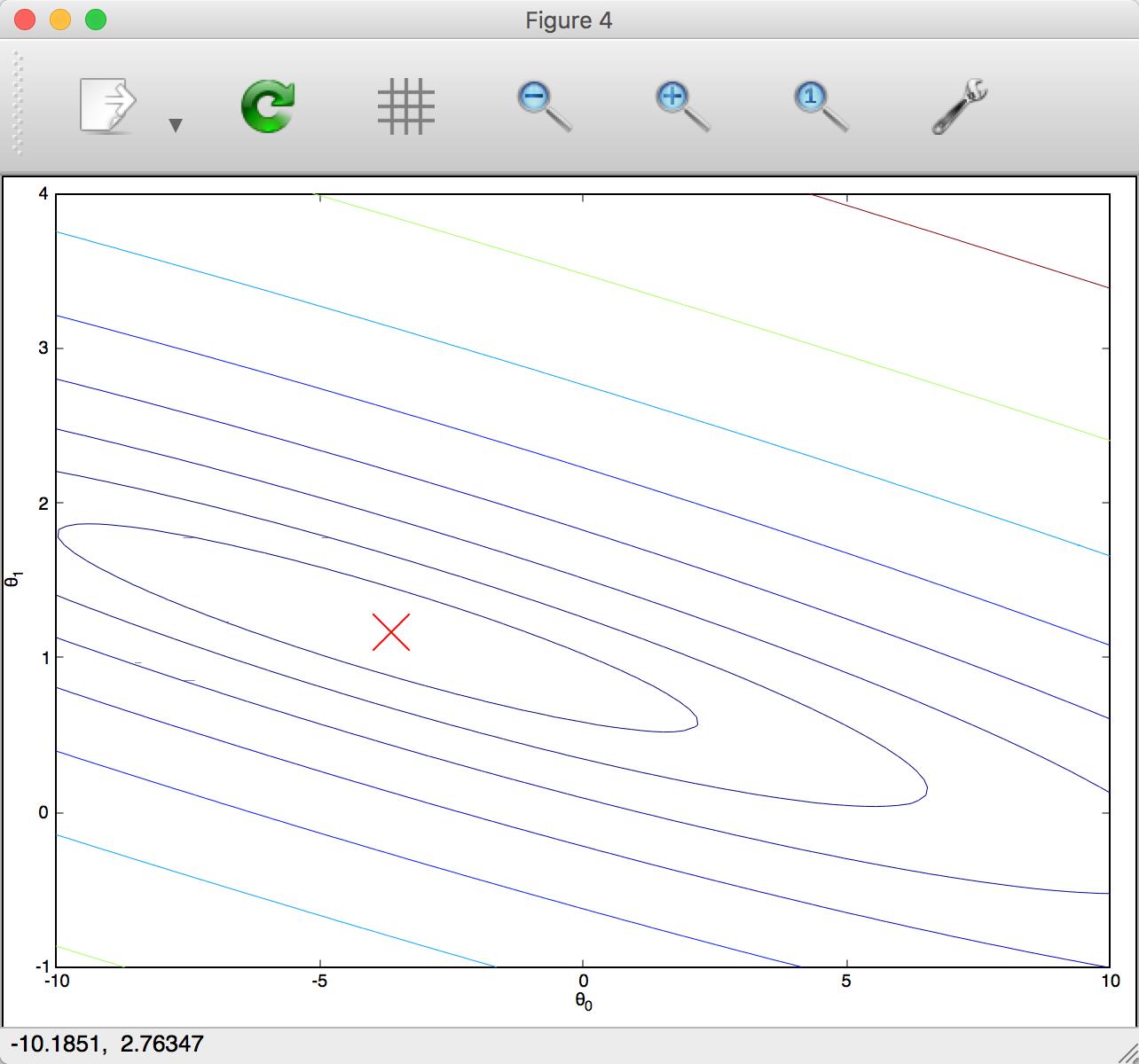
同一条线、圆上的高度（y 值）是相同的，越密的地方变化越缓慢，反之变化越剧烈。

　

featureNormalize

% ====================== YOUR CODE HERE ======================
% Instructions: First, for each feature dimension, compute the mean
%               of the feature and subtract it from the dataset,
%               storing the mean value in mu. Next, compute the 
%               standard deviation of each feature and divide
%               each feature by it\'s standard deviation, storing
%               the standard deviation in sigma. 
%
%               Note that X is a matrix where each column is a 
%               feature and each row is an example. You need 
%               to perform the normalization separately for 
%               each feature. 
%
% Hint: You might find the \'mean\' and \'std\' functions useful.
%       
% Exclude x0
mu = mean(X);
sigma = std(X);
for i=1: size(X,2),
   X(:, i) = (X(:,i)-mu(i)) / sigma(i);
end
X_norm = X;

 计算方式按照 Instructions 就可以，说一下怎么查找 Octave 的语法的。

排除 column：Octave exclude column

插入 column: Octave insert column

 

使用 for 循环完成 "divide each feature by it\'s standard deviation"

虽然这个答案提交是正确的，应该排除 X0 再放回去。

Normal Equation

inverse，表示为 ^-1 

transpose，表示为 X^T

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the code to compute the closed form solution
%               to linear regression and put the result in theta.
%

% ---------------------- Sample Solution ----------------------
theta = inverse(X\' * X) * X\' * y;