四边形不等式优化

Posted 2020-10-01 zzq

声明:

本文转载自网易博客：

　　　　http://blog.163.com/dqx_wl/blog/static/2396821452015111133052112/

四边形不等式优化_石子合并问题_C++

　　在动态规划中，经常遇到形如下式的状态转移方程：

　　　　m(i,j)=min{m(i,k-1),m(k,j)}+w(i,j)(i≤k≤j)（min也可以改为max）

　　上述的m(i,j)表示区间[i,j]上的某个最优值。w(i,j)表示在转移时需要额外付出的代价。该方程的时间复杂度为O(N³)

 　　

　　下面我们通过四边形不等式来优化上述方程，首先介绍什么是“区间包含的单调性”和“四边形不等式”

　　　　1、区间包含的单调性：如果对于 i≤i\'<j≤j\'，有 w(i\',j)≤w(i,j\')，那么说明w具有区间包含的单调性。（可以形象理解为如果小区间包含于大区间中，那么小区间的w值不超过大区间的w值）

　　　　2、四边形不等式：如果对于 i≤i\'<j≤j\'，有 w(i,j)+w(i\',j\')≤w(i\',j)+w(i,j\')，我们称函数w满足四边形不等式。（可以形象理解为两个交错区间的w的和不超过小区间与大区间的w的和）

 

　　下面给出两个定理：

　　　　1、如果上述的 w 函数同时满足区间包含单调性和四边形不等式性质，那么函数 m 也满足四边形不等式性质

　　　　　  我们再定义 s(i,j) 表示 m(i,j) 取得最优值时对应的下标（即 i≤k≤j 时，k 处的 w 值最大，则 s(i,j)=k）。此时有如下定理

　　　　2、假如 m(i,j) 满足四边形不等式，那么 s(i,j) 单调，即 s(i,j)≤s(i,j+1)≤s(i+1,j+1)。

 

　　好了，有了上述的两个定理后，我们发现如果w函数满足区间包含单调性和四边形不等式性质，那么有 s(i,j-1)≤s(i,j)≤s(i+1,j) 。

　　即原来的状态转移方程可以改写为下式：

　　　　　m(i,j)=min{m(i,k-1),m(k,j)}+w(i,j)(s(i,j-1)≤k≤s(i+1,j))（min也可以改为max）

　　由于这个状态转移方程枚举的是区间长度 L=j-i，而 s(i,j-1) 和 s(i+1,j) 的长度为 L-1，是之前已经计算过的，可以直接调用。

　　不仅如此，区间的长度最多有n个，对于固定的长度 L，不同的状态也有 n 个，故时间复杂度为 O(N^2)，而原来的时间复杂度为 O(N^3)，实现了优化！

　　今后只需要根据方程的形式以及 w 函数是否满足两条性质即可考虑使用四边形不等式来优化了。

 

　　以上描述状态用 m(i,j)，后文用的 dp[i][j]，所代表含意是相同的，特此说明。

　　以石子合并问题为例。

　　例如有６堆石子，每堆石子数依次为３ ４ ６ ５ ４ ２

　　因为是相邻石子合并，所以不能用贪心（每次取最小的两堆合并），只能用动归。（注意：环形石子的话，必须要考虑最后一堆和第一堆的合并。）

　　例如：一个合并石子的方案：

　　　　第一次合并 ３ ４ ６ ５ ４ ２ ->７

　　　　第二次合并 ７ ６ ５ ４ ２ ->１３

　　　　第三次合并 １３ ５ ４ ２ ->６

　　　　第四次合并 １３ ５ ６ ->１１

　　　　第五次合并 １３ １１ ->２４

　　总得分＝７＋６＋１１＋１３＋２４＝６１ 显然，比贪心法得出的合并方案（得分：62）更优。

　　

　　动归分析类似矩阵连乘等问题，得出递推方程：

　　　　设 dp[i][j] 表示第 i 到第 j 堆石子合并的最优值，sum[i][j] 表示第 i 到第 j 堆石子的总数量。

　　　　（可以在计算开始先做一遍求所有的 sum[i]，表示求出所有第1堆到第i堆的总数量。则 sum[i][j]=sum[j]-sum[i]。这样计算比较快。）

　　那么就有状态转移公式：

　　　　　　

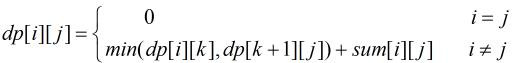
　　　　这里 i<=k<j

　　普通解法需要 O（n^3）。下面使用四边形不等式进行优化。

　　首先判断是否符合区间单调性和四边形不等式。

　　　　 i  i\'    j    j\'

　　　　3 4 6 5 4 2

　　单调性：

　　　　w[i\',j] = 4+6+5=15 w[i,j\'] =3+4+6+5+4+2=24

　　故w[i\',j] <= w[i,j\'] 满足单调性

　　四边形不等式：

　　　　w[i,j] + w[i\',j\'] = (3+4+6+5) + (4+6+5+4+2) = 18+21 = 39

　　　　w[i\',j] + w[i,j\'] = (4+6+5) + (3+4+6+5+4+2) = 15 + 24 = 39

　　　　故 w[i,j] + w[i\',j\'] <= w[i\',j] + w[i,j\']

　　故石子合并可利用四边形不等式进行优化。

 

　　利用四边形不等式，将原递推方程的状态转移数量进行压缩（即缩小了k的取值范围）。

　　令 s[i][j]=min{k | dp[i][j] = dp[i][k-1] + dp[k][j] + w[i][j]}，即计算出 dp[i][j] 时的最优的 k 值（本例中寻优为取最小）

　　也可以称为最优决策时的 k 值。由于决策 s 具有单调性，因此状态转移方程中的 k 的取值范围可修改为 :

　　　　s[i,j-1] <= s[i,j] <= s[i+1,j]

　　　　边界：s[i,i] = i

　　因为 s[i,j] 的值在 m[i,j] 取得最优值时，保存和更新，因此 s[i,j-1] 和 s[i+1,j] 都在计算 dp[i][j-1] 以及 dp[i+1][j] 的时候已经计算出来了。

　　因此，s[i][j] 即 k 的取值范围很容易确定。

　　根据改进后的状态方程，以及 s[i][j] 的定义方程，可以很快的计算出所有状态的值。计算过程可以如下表所示（类似于矩阵连乘的打表）。

　　状态表（如果是环形石子合并，需要打2n*2n的表）

　　　　3 4 6 5 4 2

　　

　　例如：

　　　　计算dp[1][3]，由于s[1][2]=1，s[2][3]=2，则k值的取值范围是1<=k<=2

　　　　则，dp[1][3]=min{dp(1,1)+dp(2,3)+13, dp(1,2)+dp(3,3)+13}=min{10+13, 7+13}=20，将其填到状态表。同时，由于取最优值的k等于2，则将其填到s表。

　　　　同理，可以计算其他状态表和s表中的值。

　　　　　　dp[2][4]=min{dp(2,2)+dp(3,4)+15, dp(2,3)+dp(4,4)+15}=min{11+15, 10+15}=25

　　　　　　k=3

　　　　从表中可以看出，当计算dp[2][5]的时候，由于s[ i,j-1]=s[ 2,4]=3，s[ i+1,j]=s[3,5]=3，此时k的取值范围已经限定为只有一个，大幅缩短了寻找最优解的时间。

 

　　这里给出程序代码：

 1 #include<iostream>
 2 #include<cstdio>
 3 using namespace std;
 4 
 5 const int N=205;
 6 const int INF=0x7fffffff;
 7 int n;
 8 int a[N],sum[N],dp[N][N],s[N][N];
 9 void f(); 
10 int main()
11 {
12      while(~scanf("%d",&n))
13      {
14          sum[0]=0;
15         for (int i=1;i<=n;i++)
16         {
17             scanf("%d",&a[i]);
18             sum[i]=sum[i-1]+a[i];
19         }
20         f();
21         printf("%d\\n",dp[1][n]);
22      }
23      return 0;
24 
25 }
26 void f()
27 {
28      for (int i=1;i<=n;i++) dp[i][i]=0,s[i][i]=i;
29      for (int r=1;r<n;r++)
30      {
31          for (int i=1;i<n;i++)
32         {
33             int j=i+r;
34             if(j>n) break;
35             dp[i][j]=INF;
36             for (int k=s[i][j-1];k<=s[i+1][j];k++)
37             {
38                 if(dp[i][j]>dp[i][k]+dp[k+1][j])
39                 {
40                     dp[i][j]=dp[i][k]+dp[k+1][j];
41                     s[i][j]=k;
42                 }
43             }
44             dp[i][j]+=sum[j]-sum[i-1];
45         }
46     }
47 }