最短路luoguP1027Car的旅行路线

Posted 2020-10-01

Car的旅行路线

题目描述

又到暑假了，住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场，分别位于一个矩形的四个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第I个城市中高速铁路了的单位里程价格为Ti，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为t。

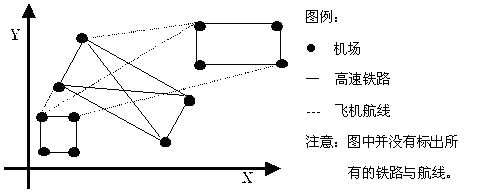
 　　那么Car应如何安排到城市B的路线才能尽可能的节省花费呢？她发现这并不是一个简单的问题，于是她来向你请教。

找出一条从城市A到B的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

输入输出格式

输入格式：

第一行为一个正整数n(0<=n<=10)，表示有n组测试数据。

每组的第一行有四个正整数s，t，A，B。

S(0<S<=100)表示城市的个数，t表示飞机单位里程的价格，A，B分别为城市A，B的序号，(1<=A，B<=S)。

接下来有S行，其中第I行均有7个正整数xi1，yi1，xi2，yi2，xi3，yi3，Ti，这当中的(xi1，yi1)，(xi2，yi2)，(xi3，yi3)分别是第I个城市中任意三个机场的坐标，T I为第I个城市高速铁路单位里程的价格。

 

输出格式：

共有n行，每行一个数据对应测试数据。 保留一位小数

 

俺的题解

向量求第四点+SPFA

本人求第四点的方式好像有点麻烦= =

　　先用向量求出三个点中的直角点，然后通过确定位置后的三点坐标计算第四点。

                              

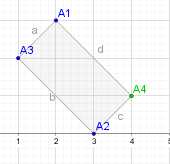
                     图中A3为直角点，x4=x1+x2-x3    y4=y1+y2-y3

 

存边比较巧妙。每个机场占一个点，于是每个城市占了4个位置。直接暴力循环把火车和飞机的边一块存了...

还有，注意是无向边，可能只有我会犯这么sb的错误= =

从起点城市的4个机场分别SPFA，共4次。取终点城市4个机场的最小值即为答案。

俺的代码

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<queue>
  5 #include<cmath>
  6 #include<vector>
  7 using namespace std;
  8 #define INF 1000000000.0
  9 int tt,s,t,a,b;
 10 int prize[170];
 11 double d[20000];
 12 struct cc
 13 {
 14     int x,y,p;
 15 }city[170][5];
 16 struct vec
 17 {
 18     int x,y;
 19     int p,q; 
 20 };
 21 struct node
 22 {
 23     int v;
 24     double w;
 25 };
 26 vector<node> edge[20000];
 27 int count(int k)//求第四点 
 28 {
 29     int c=0;vec v[5];
 30     for(int i=1;i<3;i++)
 31     {
 32         for(int j=i+1;j<=3;j++)
 33         {
 34             c++;
 35             v[c].x=city[k][i].x-city[k][j].x;
 36             v[c].y=city[k][i].y-city[k][j].y;
 37             v[c].p=i;
 38             v[c].q=j;
 39         }
 40     } 
 41     bool sol=0;
 42     for(int i=1;i<c;i++)
 43     {
 44         for(int j=i+1;j<=c;j++)
 45         {
 46             if((v[i].x*v[j].x)+(v[i].y*v[j].y) == 0)
 47             {
 48                 int wei[5]={0},zu=0;
 49                 wei[v[i].p]++;wei[v[i].q]++;
 50                 wei[v[j].p]++;wei[v[j].q]++;
 51                 int oth[2]={0},cc=0;
 52                 for(int w=1;w<=3;w++){
 53                     if(wei[w] == 2)
 54                         zu=w;
 55                     else
 56                         oth[++cc]=w;
 57                 }
 58                 if(city[k][oth[1]].x  > city[k][oth[2]].x ||(city[k][oth[1]].x  == city[k][oth[2]].x && city[k][oth[1]].y  > city[k][oth[2]].y ))
 59                 {
 60                     int temp=oth[2];
 61                     oth[2]=oth[1];
 62                     oth[1]=temp;
 63                 }
 64 
 65                 city[k][4].x=city[k][oth[1]].x+city[k][oth[2]].x-city[k][zu].x;
 66                 city[k][4].y=city[k][oth[1]].y+city[k][oth[2]].y-city[k][zu].y;
 67                 sol=1;
 68                 break;
 69             }
 70         }
 71         if(sol==1)break;
 72     }
 73 }
 74 
 75 double countdis(int i,int n1,int j,int n2)
 76 {
 77     return sqrt((city[i][n1].x-city[j][n2].x)*(city[i][n1].x-city[j][n2].x)
 78                +(city[i][n1].y-city[j][n2].y)*(city[i][n1].y-city[j][n2].y));
 79 }
 80 void SPFA(int a)
 81 {
 82     for(int i=0;i<=4*s+1;i++)
 83     {
 84         d[i]=INF;
 85     }
 86     queue<int>q;
 87     q.push(a);
 88     d[a]=0.0;
 89     while(!q.empty())
 90     {
 91         int x=q.front();q.pop();
 92         for(int i=0;i<edge[x].size();i++)
 93         {
 94             int v=edge[x][i].v;
 95             double w=edge[x][i].w;
 96             if(d[x]+w < d[v])
 97             {
 98                 d[v]=d[x]+w;
 99                 q.push(v);
100             }
101         }
102     }
103 }
104 int main()
105 {
106     scanf("%d",&tt);
107     while(tt--)
108     {
109     scanf("%d%d%d%d",&s,&t,&a,&b);
110     for(int i=1;i<=s;i++)
111     {
112         for(int j=1;j<=3;j++)
113         {
114             int x,y;scanf("%d%d",&x,&y);
115             city[i][j].x=x;
116             city[i][j].y=y;
117         }
118         count(i);
119         scanf("%d",&prize[i]);
120     }
121 
122     for(int i=1;i<=s;i++)
123     {
124         for(int k1=1;k1<=4;k1++)
125         {
126             for(int j=1;j<=s;j++)
127             {
128                 for(int k2=1;k2<=4;k2++)
129                 {
130                     if(i == j && k1 < k2)
131                     {
132                         node p;
133                         p.v=(j-1)*4+k2;
134                         p.w=countdis(i,k1,j,k2)*prize[i];
135                         edge[(i-1)*4+k1].push_back(p);
136                         node q;
137                         q.v=(i-1)*4+k1;
138                         q.w=p.w;
139                         edge[(j-1)*4+k2].push_back(q);
140                     }
141                     if(i != j)
142                     {
143                         node p;
144                         p.v=(j-1)*4+k2;
145                         p.w=countdis(i,k1,j,k2)*t;
146                         edge[(i-1)*4+k1].push_back(p);
147                         node q;
148                         q.v=(i-1)*4+k1;
149                         q.w=p.w;
150                         edge[(j-1)*4+k2].push_back(q);
151                     }
152                 }
153             }
154         }
155     }
156     double ans=1000000000.0;
157     for(int i=1;i<=4;i++)
158     {
159         SPFA((a-1)*4+i);
160         for(int j=1;j<=4;j++)
161         {
162             ans=min(ans,d[(b-1)*4+j]);
163         }
164     }
165     printf("%.1lf\\n",ans);
166     }
167     return 0;
168 }

点击查看