洛谷P1027 Car的旅行路线

Posted 2020-10-03 范仁义

洛谷P1027 Car的旅行路线

题目描述

又到暑假了，住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场，分别位于一个矩形的四个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第I个城市中高速铁路了的单位里程价格为Ti，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为t。

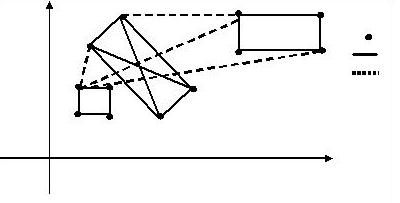
图例（从上而下）

机场 高速铁路

飞机航线

　 注意：图中并没有

标出所有的铁路与航线。

那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题，于是她来向你请教。

找出一条从城市A到B的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

输入输出格式

输入格式：

 

第一行为一个正整数n(0<=n<=10)，表示有n组测试数据。

每组的第一行有四个正整数s，t，A，B。

S(0<S<=100)表示城市的个数，t表示飞机单位里程的价格，A，B分别为城市A，B的序号，(1<=A，B<=S)。

接下来有S行，其中第I行均有7个正整数xi1，yi1，xi2，yi2，xi3，yi3，Ti，这当中的(xi1，yi1)，(xi2，yi2)，(xi3，yi3)分别是第I个城市中任意三个机场的坐标，T I为第I个城市高速铁路单位里程的价格。

 

输出格式：

 

共有n行，每行一个数据对应测试数据。 保留一位小数

 

输入输出样例

输入样例#1：

1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3

输出样例#1：

47.5

 

二、分析

直接算出各个机场之间的费用即可，然后用dijkstra做，这题floyed也可以过。

对于题目每个机场给三个点，我们需要用迭代法不断交换三个点的位置:A-B-C --> B-C-A --> C-A-B使其满足矩形关系。

判断矩形我们可以用垂直关系。

 

 1 #include <iostream>  
 2 #include <cstring>  
 3 #include <iomanip>  
 4 #include <cmath>  
 5 #include <algorithm>  
 6 #define INF 10000000  
 7 #define CTOA(x) (((x-1)<<2)+1)   
 8 #define DISTANCE(x1,y1,x2,y2) ((double)sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))) //自定义宏，开根号操作  
 9 using namespace std;  
10 double node[4050][4050]; //node[i][j]=i点到j点的最短距离  
11 double T; //t=飞机航线的单价，T=铁路线路的单价  
12 int tx[3],ty[3],t;  
13 double ans=INF;  
14 struct city  
15 {  
16     int x[4];  
17     int y[4];  
18 }ct[105]; //ct[i].x[j]=第i个城市第j个机场横坐标，ct[i].y[j]=第i个城市第j个机场纵坐标  
19 void getfour(int c) //获取第c个城市第四个机场的坐标  
20 {  
21     int tt;  
22     memcpy(tx,ct[c].x,sizeof(tx));  
23     memcpy(ty,ct[c].y,sizeof(ty));  
24     while((tx[0]-tx[1])*(tx[2]-tx[1])+(ty[0]-ty[1])*(ty[2]-ty[1])) //(x1-x2)*(x3-x2)=(y1-y2)*(y3-y2)时，两直线垂直  
25     {  
26         tt=tx[0]; tx[0]=tx[1]; tx[1]=tx[2]; tx[2]=tt;  
27         tt=ty[0]; ty[0]=ty[1]; ty[1]=ty[2]; ty[2]=tt; //点ABC转化为BCA，不断迭代到AB⊥BC  
28     }  
29     ct[c].x[3]=tx[0]-tx[1]+tx[2];  
30     ct[c].y[3]=ty[0]-ty[1]+ty[2];  
31 }  
32 int min(int a1,int b1)  
33 {  
34     if(a1<b1) return a1;  
35     return b1;  
36 }  
37 int main()  
38 {  
39     int i,j,k,l,m,n;  
40     scanf("%d",&n);  
41     while(n--)  
42     {  
43         int s,t,a,b;  
44         cin>>s>>t>>a>>b;  
45         if(a==b) { cout<<"0.0\n"; continue;} //注意出发点和目的地在同一城市的情况，直接输出0.0  
46         int airport=s<<2; //airport=机场数量  
47         for(i=1;i<=airport;i++)  
48         {  
49             for(j=1;j<=airport;j++)  
50                 node[i][j]=INF; //初始化各点间的路的距离为无穷大  
51         }  
52         for(i=1;i<=s;i++)  
53         {  
54             for(j=0;j<3;j++)  
55                 cin>>ct[i].x[j]>>ct[i].y[j];  
56             cin>>T;  
57             getfour(i); //将第i个城市第四个机场确定  
58             for(j=0;j<4;j++)  
59             {  
60                 for(k=0;k<4;k++)  
61                     if(j!=k) //不是同一个机场的话，勾股定理初始化二者间的花费（花费=距离*每单位路程单价）  
62                         node[CTOA(i)+j][CTOA(i)+k]=(DISTANCE(ct[i].x[j],ct[i].y[j],ct[i].x[k],ct[i].y[k])*T);  
63             }  
64         }  
65         for(i=1;i<=s;i++)  
66         {  
67             for(j=1;j<=s;j++)  
68             {  
69                 if(i!=j) //如果i、j不是同一个城市  
70                     for(k=0;k<4;k++) //第i个城市的第k个机场  
71                     {  
72                         for(l=0;l<4;l++) //第j个城市的第l个机场  
73                             node[CTOA(i)+k][CTOA(j)+l]=(DISTANCE(ct[i].x[k],ct[i].y[k],ct[j].x[l],ct[j].y[l])*t);  
74                     }  
75             }  
76         }  
77         //Floyd  
78         for(k=1;k<=airport;k++)  
79         {  
80             for(i=1;i<=airport;i++)  
81             {  
82                 for(j=1;j<=airport;j++)  
83                 {  
84                     node[i][j]=min(node[i][j],node[i][k]+node[k][j]);  
85                 }  
86             }  
87         }  
88         for(i=0;i<4;i++)  
89         {  
90             for(j=0;j<4;j++)  
91                 ans=min(ans,node[CTOA(a)+i][CTOA(b)+j]);  
92         }  
93         cout<<setiosflags(ios::fixed)<<setprecision(1)<<ans<<endl;  
94     }  
95     return 0;  
96 }