HDU 6069 Counting Divisors —— 2017 Multi-University Training 4
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了HDU 6069 Counting Divisors —— 2017 Multi-University Training 4相关的知识,希望对你有一定的参考价值。
Counting Divisors
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 2599 Accepted Submission(s): 959
Problem Description
In mathematics, the function d(n) denotes the number of divisors of positive integer n.
For example, d(12)=6 because 1,2,3,4,6,12 are all 12‘s divisors.
In this problem, given l,r and k, your task is to calculate the following thing :
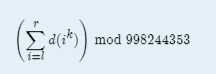
For example, d(12)=6 because 1,2,3,4,6,12 are all 12‘s divisors.
In this problem, given l,r and k, your task is to calculate the following thing :
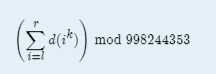
Input
The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.
In each test case, there are 3 integers l,r,k(1≤l≤r≤1012,r?l≤106,1≤k≤107).
In each test case, there are 3 integers l,r,k(1≤l≤r≤1012,r?l≤106,1≤k≤107).
Output
For each test case, print a single line containing an integer, denoting the answer.
Sample Input
3
1 5 1
1 10 2
1 100 3
Sample Output
10
48
2302
题目大意:d(i)是 i 的因数个数,让我们求 l<=i<=r 时,d(i^k)之和.
思路:对一个数n=p1t1*p2t2*...*pntn, pi是n的质因数。则n的因数个数是(t1+1)*(t2+1)*...*(tn-1+1)*(tn+1), 易得i^k的因数个数是(k*t1+1)*(k*t2+1)*...*(k*tn+1),那么接下来就是要对 i 进行质因数分解了。 在打表打出质因数后,分解时对于一个质数P, 在[l , r]区间内所有能整除P的数进行质因数分解,这样能保证不会有多余时间花在搜索质因数上,这种做法类似筛法。具体见代码。
AC代码(标程):
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #include<stdio.h> 6 #define it (p-l) 7 using namespace std; 8 typedef long long LL; 9 const LL MOD=998244353; 10 const long long MAXN=1000005; 11 long long prime[MAXN],tot=0; 12 bool isPrime[MAXN]; 13 LL k,num[MAXN],res[MAXN]; 14 void getprime(){ 15 memset(isPrime, true, sizeof(isPrime)); 16 for(int i=2;i<MAXN;i++){ 17 if(isPrime[i]){ 18 prime[++tot]=i; 19 } 20 for(int j=1;j<=tot;j++){ 21 if(i*prime[j]>MAXN) break; 22 isPrime[i*prime[j]]=false; 23 if(i%prime[j]==0) break; 24 } 25 } 26 return ; 27 } 28 LL cal(LL l, LL r) 29 { 30 LL ans=0,tmp,cnt; 31 for(int i=1;i<=tot;i++) 32 { 33 LL p=(l+prime[i]-1)/prime[i]*prime[i]; 34 while(p<=r){ 35 cnt=0; 36 while(num[it]%prime[i]==0){ 37 num[it]/=prime[i]; 38 cnt++; 39 } 40 res[it]=res[it]*(k*cnt+1)%MOD; 41 p+=prime[i]; 42 } 43 } 44 for(LL p=l;p<=r;p++){ 45 if(num[it]==1) 46 ans+=res[it]; 47 else 48 ans+=res[it]*(k+1); 49 ans%=MOD; 50 } 51 return ans; 52 } 53 int main() 54 { 55 int T; 56 LL l,r; 57 getprime(); 58 scanf("%d", &T); 59 while(T--) 60 { 61 scanf("%lld %lld %lld", &l, &r, &k); 62 for(LL p=l;p<=r;p++){ 63 res[it]=1; 64 num[it]=p; 65 } 66 LL res=cal(l, r); 67 printf("%lld\\n", res); 68 } 69 }
以上是关于HDU 6069 Counting Divisors —— 2017 Multi-University Training 4的主要内容,如果未能解决你的问题,请参考以下文章
hdu 6069 Counting Divisors(求因子的个数)
HDU 6069 Counting Divisors(唯一分解定理+因子数)
第四场 hdu 6069 Counting Divisors (逆向思维)