HDU 6069 Counting Divisors（唯一分解定理+因子数）

Posted 2020-10-01 谦谦君子，陌上其华

http://acm.hdu.edu.cn/showproblem.php?pid=6069

题意：

 

思路：

根据唯一分解定理，$n={a_{1}}^{p1}*{a2_{}}^{p2}...*{a_{m}}^{pm}$，那么n的因子数就是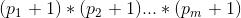

n的k次方也是一样的，也就是p前面乘个k就可以了。

先打个1e6范围的素数表，然后枚举每个素数，在[ l , r ]寻找该素数的倍数，将其分解质因数。

到最后如果一个数没有变成1，那就说明这个数是大于1e6的质数。（它就只有0和1两种选择）

 1 #include<iostream>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cstdio>
 5 #include<sstream>
 6 #include<vector>
 7 #include<stack>
 8 #include<queue>
 9 #include<cmath>
10 #include<map>
11 #include<set>
12 using namespace std;
13 typedef long long ll;
14 typedef pair<int,int> pll;
15 const int INF = 0x3f3f3f3f;
16 const int maxn=1e6+5;
17 const int mod=998244353;
18 
19 int n;
20 int cnt=0;
21 int primes[maxn];
22 int vis[maxn];
23 
24 void get_primes()
25 {
26     int m=sqrt(maxn+0.5);
27     for(int i=2;i<=m;i++)
28     {
29         if(!vis[i])
30         {
31             for(int j=i*i;j<=maxn;j+=i)
32                 vis[j]=1;
33         }
34     }
35     for(int i=2;i<=maxn;i++)
36         if(!vis[i])   primes[cnt++]=i;
37 }
38 
39 ll l, r, k;
40 ll sum[maxn], num[maxn];
41 
42 int main()
43 {
44     //freopen("in.txt","r",stdin);
45     get_primes();
46     int T;
47     scanf("%d",&T);
48     while(T--)
49     {
50         scanf("%lld%lld%lld",&l,&r,&k);
51 
52         ll ans=0;
53         for(ll i=l;i<=r;i++)  {sum[i-l]=1;num[i-l]=i;}
54 
55         for(int i=0; i<cnt && primes[i]*primes[i]<=r; i++)
56         {
57             ll tmp=ceil((long double)l/primes[i])*primes[i];
58             for(ll j=tmp;j<=r;j+=primes[i])
59             {
60                 if(num[j-l]%primes[i]==0)
61                 {
62                     int res=0;
63                     while(num[j-l]%primes[i]==0)
64                     {
65                         res++;
66                         num[j-l]/=primes[i];
67                     }
68                     sum[j-l]=(sum[j-l]*(((ll)res*k+1))%mod)%mod;
69                 }
70             }
71         }
72 
73         for(ll i=l;i<=r;i++)
74         {
75             if(num[i-l]!=1)   sum[i-l]=(sum[i-l]*(k+1))%mod;  //大于1e6的质数
76             ans=(ans+sum[i-l])%mod;
77         }
78         printf("%lld\\n",ans);
79     }
80     return 0;
81 }