HDU 6069 Counting Divisors

Posted 2020-10-01 MeowMeowMeow

// 变量命名很重要 你看我抄队友的代码抄一遍就t了 再改还是t 我以为是我不够大力 原来是这个变量名弄的太混乱了- -搞了好半天才发现哈哈 

//有一个很重要的定理是一个数的因数个数和他的素数幂次乘积表达式的关系 哈哈

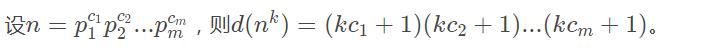
当时比赛如果能想到并推出来这个 我想我们也是那200的分子了。。唉- -简单的素数题还是脑子想不开 比完赛要把知识点整理一下 好好搞下专题

还有我的素数筛好像比他的慢了100ms- -有点害怕

#include <iostream>
#include <algorithm>
#include <stdio.h>
#include <queue>
#include <limits.h>
#include <string.h>
#include <vector>
#include <map>
#include <math.h>
#define LL long long
#define INF 2100000000
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define eps 5e-7
using namespace std;
const int maxn=(int)1e6 +30;
const int MOD=998244353;
const int MAXN=(int )1e6;
LL prime[MAXN];
bool p[MAXN];
int getprime(){
    memset(prime,0,sizeof prime);
    for(int i=2;i<MAXN;i++){
        if(!prime[i]) prime[++prime[0]]=i;
        for(int j=1;j<=prime[0]&&prime[j]<=MAXN/i;j++){
            prime[prime[j]*i]=1;
            if(i%prime[j]==0)break;
        }
    }
    return prime[0];
}
int siever()
{
    for(int i=0;i<1000;i++)
        for(int k=(i<<1)+3,j=k*i+k+i;j<600000;j+=k)
            p[j]=1;
    int sp=1;
    for(int i=0;i<600000;i++)
        if(!p[i])prime[sp++]=(i<<1)+3;
    prime[0]=2;
    return sp;
}
LL a[maxn];
LL d[maxn];
int main(){
#ifdef shuaishuai
    freopen("C:\\\\Users\\\\hasee\\\\Desktop\\\\a.txt","r",stdin);
    //freopen("C:\\\\Users\\\\hasee\\\\Desktop\\\\b.txt","w",stdout);
#endif
    int pcnt=getprime();
    int t;
    scanf("%d",&t);
    while(t--){
        LL L,R,K;
        LL ans=0;
        scanf("%lld%lld%lld",&L,&R,&K);

        LL ed=sqrt(R)+1;
        LL beg=L;
        int r=0;
        while(L<=R){
            d[r]=1;
            a[r++]=L;
            L++;
        }
       // printf("%lld %d\\n",a[0],tot);

        for(int i=1;prime[i]<=ed&&i<=pcnt;i++){
            LL tmp=beg%prime[i];
            int l=(tmp==0)? 0: (prime[i]-tmp);
            while(l<r){
                //printf("l: %d prime i\\n",l);
                LL cnt=0;
                while(a[l]!=0&&a[l]%prime[i]==0){
                    a[l]/=prime[i];
                    cnt++;
                }
                d[l]*=(cnt*K+1LL);
                d[l]%=MOD;
                l+=(int)prime[i];
            }
        }
        for(int i=0;i<r;i++){
            if(a[i]>1) d[i]*=(K+1);//a[i]是个质数- -它的k次的因数就是1*（k+1）
            ans=(ans+d[i])%MOD;
        }

       // for(int i=0;i<tot;i++)printf("%d %lld %lld\\n",i+1,a[i],d[i]);
        printf("%lld\\n",ans);
    }
    return 0;
}