最短路径——Floyd算法

Posted 2020-10-01 GGBeng

一、相关介绍

最短路径

• 从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径。

Floyd算法

• Warshall算法的扩展
• 三个for循环就可以解决问题
• 时间复杂度为O(n³)

二、算法介绍

【打基础】

无向带权图G

Dis(AB)    节点A到节点B的最短路径的距离

辅助数组path[]　　用于求最短路径过程中记录节点

【基本思想】

问题：从图G上任选一节点A，试求出A到节点B的最短路径以及Dis(AB) 。

分析：从节点A到节点B的最短路径只有2种可能：

1. 直接从A到B
2. 从A经过若干个节点再到B

过程：首先从节点A出发，对于每一个与A邻接的节点X，我们检查不等式Dis(AX) + Dis(XB) < Dis(AB)是否成立？

• 如果成立，证明从A到X再到B的路径比A直接到B的路径短，我们便设置Dis(AB) = Dis(AX) + Dis(XB)，这样一来，在我们遍历所有可能的节点X的同时，Dis(AB)的值会不断更新，当所有节点X被遍历完时，Dis(AB)中记录的便是A到B的最短路径的距离。

很简单啊，且慢，来一小段代码：

for ( int i = 0; i < 节点个数; ++i )
{
	for ( int j = 0; j < 节点个数; ++j )
	{
		for ( int k = 0; k < 节点个数; ++k )
		{
			if ( Dis[i][k] + Dis[k][j] < Dis[i][j] )
			{
				// 找到更短路径
				Dis[i][j] = Dis[i][k] + Dis[k][j];
			}
		}
	}
}

注意！！这里我们要注意循环的嵌套顺序，如果把检查所有节点X放在最内层，那么结果将是不正确的，为什么呢？因为这样便过早的把i到j的最短路径确定下来了，而当后面存在更短的路径时，已经不再会更新了。

让我们来看一个例子，看下图：

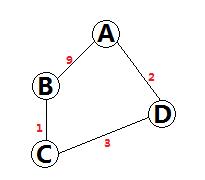//图中红色的数字代表边的权重

如果我们在最内层检查所有节点X，那么对于A->B，我们只能发现一条路径，就是A->B，路径距离为9。而这显然是不正确的，真实的最短路径是A->D->C->B，路径距离为6。

造成错误的原因就是我们把检查所有节点X放在最内层，造成过早的把A到B的最短路径确定下来了，当确定A->B的最短路径时Dis(AC)尚未被计算。

所以，我们需要改写循环顺序，如下：

for ( int k = 0; k < 节点个数; ++k )
{
	for ( int i = 0; i < 节点个数; ++i )
	{
		for ( int j = 0; j < 节点个数; ++j )
		{
			if ( Dis[i][k] + Dis[k][j] < Dis[i][j] )
			{
				// 找到更短路径
				Dis[i][j] = Dis[i][k] + Dis[k][j];
			}
		}
	}
}

如果还是看不懂，那就用草稿纸模拟一遍，之后你就会豁然开朗。半个小时足矣（早知道的话会节省很多个半小时了）。

我们再举个例子看看两者的差别：

①循环顺序是i-j-k

如果我们现在要更新的1-4的最短距离，要枚举经过的城市个数，有0,1,2,3,4,5种情况，假如现在2-3城市的最短距离为10，当经过的城市为2时候，发现2-3的最短距离为10，可能比其他大了，所以经过2个城市的最小距离可能为8，上面6种情况更新后发现1-4最短距离为13.

当继续更新时，我们更新后2-3的最短距离竟然为1，但是我们再也回不到1-4这种情况了。所以，1-4的最短距离明显就是错误的。

②循环顺序是k-i-j

我们更新1-4的时候，2-3可能没更新，但是1-4可以更新k次，即使不是最短的，以后再更新到的时候就可以更新为最短了。所以这种才是正确的方法。

综上，对于每一个节点X，我们都会把所有的i到j处理完毕后才继续检查下一个节点。

【寻找最短路径】

• Path数组的用法：如果Path(AB)的值为P，则表示A节点到B节点的最短路径是A->...->P->B

因此，假设我们要找A->B的最短路径，那么就依次查找，假设Path(AB)的值为P，那么接着查找Path(AP)，假设Path(AP)的值为L，那么接着查找Path(AL)，假设Path(AL)的值为A，则查找结束，最短路径为A->L->P->B。

• 那么，如何填充Path的值呢？

很简单，当我们发现不等式Dis(AX) + Dis(XB) < Dis(AB)成立时，就要把最短路径改为A->...->X->...->B，而此时，Path(XB)的值是已知的，所以，Path(AB) = Path(XB)。

【测试代码】

#include<cstdio>
#include<cmath>
#include<cstring>
#include<string>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<map>
#include<set>
using namespace std;
#define INFINITE 1000			// 最大值
#define MAX_VERTEX_COUNT 20// 最大顶点个数
//////////////////////////////////////////////////////////////////////////

struct Graph
{
	int		arrArcs[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT];	// 邻接矩阵
	int		nVertexCount;								// 顶点数量
	int		nArcCount;									// 边的数量
};
//////////////////////////////////////////////////////////////////////////

void readGraphData( Graph *_pGraph )
{
	std::cout << "请输入顶点数量和边的数量: ";
	std::cin >> _pGraph->nVertexCount;
	std::cin >> _pGraph->nArcCount;

	std::cout << "请输入邻接矩阵数据:" << std::endl;
	for ( int row = 0; row < _pGraph->nVertexCount; ++row )
	{
		for ( int col = 0; col < _pGraph->nVertexCount; ++col )
		{
			std::cin >> _pGraph->arrArcs[row][col];
		}
	}
}

void floyd( int _arrDis[][MAX_VERTEX_COUNT], int _arrPath[][MAX_VERTEX_COUNT], int _nVertexCount )
{
	// 先初始化_arrPath
	for ( int i = 0; i < _nVertexCount; ++i )
	{
		for ( int j = 0; j < _nVertexCount; ++j )
		{
			_arrPath[i][j] = i;
		}
	}
	//////////////////////////////////////////////////////////////////////////

	for ( int k = 0; k < _nVertexCount; ++k )
	{
		for ( int i = 0; i < _nVertexCount; ++i )
		{
			for ( int j = 0; j < _nVertexCount; ++j )
			{
				if ( _arrDis[i][k] + _arrDis[k][j] < _arrDis[i][j] )
				{
					// 找到更短路径
					_arrDis[i][j] = _arrDis[i][k] + _arrDis[k][j];

					_arrPath[i][j] = _arrPath[k][j];
				}
			}
		}
	}
}

void printResult( int _arrDis[][MAX_VERTEX_COUNT], int _arrPath[][MAX_VERTEX_COUNT], int _nVertexCount )
{
	std::cout << "Origin -> Dest	Distance	Path" << std::endl;

	for ( int i = 0; i < _nVertexCount; ++i )
	{
		for ( int j = 0; j < _nVertexCount; ++j )
		{
			if ( i != j )	// 节点不是自身
			{
				std::cout << i+1 << " -> " << j+1 << "\\t\\t";
				if ( INFINITE == _arrDis[i][j] )	// i -> j 不存在路径
				{
					std::cout << "INFINITE" << "\\t\\t";
				}
				else
				{
					std::cout << _arrDis[i][j] << "\\t\\t";

					// 由于我们查询最短路径是从后往前插，因此我们把查询得到的节点
					// 压入栈中，最后弹出以顺序输出结果。
					std::stack<int> stackVertices;
					int k = j;
					
					do 
					{
						k = _arrPath[i][k];
						stackVertices.push( k );
					} while ( k != i );
					//////////////////////////////////////////////////////////////////////////

					std::cout << stackVertices.top()+1;
					stackVertices.pop();

					unsigned int nLength = stackVertices.size();
					for ( unsigned int nIndex = 0; nIndex < nLength; ++nIndex )
					{
						std::cout << " -> " << stackVertices.top()+1;
						stackVertices.pop();
					}

					std::cout << " -> " << j+1 << std::endl;
				}
			}
		}
	}
}

int main()
{
	Graph myGraph;
	readGraphData( &myGraph );
	//////////////////////////////////////////////////////////////////////////

	int arrDis[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT];
	int arrPath[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT];

	// 先初始化arrDis
	for ( int i = 0; i < myGraph.nVertexCount; ++i )
	{
		for ( int j = 0; j < myGraph.nVertexCount; ++j )
		{
			arrDis[i][j] = myGraph.arrArcs[i][j];
		}
	}

	floyd( arrDis, arrPath, myGraph.nVertexCount );
	//////////////////////////////////////////////////////////////////////////

	printResult( arrDis, arrPath, myGraph.nVertexCount );
	//////////////////////////////////////////////////////////////////////////

	return 0;
}