图的最短路径的Dijkstra算法及Floyd算法

Posted 2021-12-18 薛定谔的猫ovo

文章目录

• • 最短路径的概念
  • 求单源最短路径的Dijkstra算法
  • 求各个顶点之间最短路径的Floyd算法
  • 完整代码

---

最短路径的概念

 在一个无权图中，若从一个顶点到另一个顶点存在着一条路径（仅限于无回路的简单路径），则该路径上的边数即为路径长度，等于该路径上的顶点数减一。
 从一个顶点到另一个顶点所有可能的路径中，路径长度最短（即经过的边数最少）的路径称为最短路径，其路径长度叫做最短路径长度或最短距离。

 在一个带权图中，从一个顶点v到另一个顶点u的路径上所经过各边上的权值之和即为该路径的带权路径长度，从v到u可能不止一条路径，把带权路径长度最短（即其值最小）的那条路径称作是最短路径，其权值之和称作最短路径长度或最短距离。

---

求单源最短路径的Dijkstra算法

Dijstra算法用于求图中一个顶点到其余各顶点的最短路径。
算法设置

• 一个集合$S$，记录已经求的最短路径的顶点；
• 一个辅助数组$dist[]$，$dist[i]$存放集合$S$内顶点到集合$S$外顶点$i$的最短距离，即源点到其他各顶点的当前最短路径长度。
• 一个辅助数组$path[]$，$path[i]$记录集合$S$外顶点$i$距离集合$S$内哪个顶点最近，即源点到顶点$i$之间的最短路径的前驱结点，在算法结束时，可以根据其值追溯得到源点到顶点$v_i$的最短路径。
  
  

算法步骤：

• 假设从选择从顶点0出发，即$u$=0，则S内最初只有一个顶点0， $S[0]$ = 1。
• 再令$path[0]$= -1，其他$path[i]$= 0，表示集合S外各个顶点$i$距离集合$S$内顶点0最近。
• 数组$dist[i]$ = G.Edge$[0][i]$，表示源点0（集合内顶点）到顶点$i$的最短距离。如果$dist[i]$ = $maxweight$，则表示没有到顶点$i$的路径。然后重复以下工作：
  • 在$dist[]$中选择满足$S[i]$ = 0的$dist[i]$最小的顶点$i$，用$v$标记它。则选中的路径长度最短的边为<$path[v],v$>，相应的最短路径为$dist[v]$。
  • 让$S[v]$ = 1，表示它已经加入集合$S$。
  • 取$dist[i]=mindist[i],dist[v]$ + G.Edge$[v][i]$。即检查集合$S$外各顶点$i$，如果绕过顶点v到顶点i的距离$dist[v]$ + G.Edge$[v][i]$比原来集合$S$中顶点到顶点$i$的的最短距离$dist[i]$还要小，则修改到顶点$i$的最短距离为$dist[v]$ + G.Edge$[v][i]$，同时修改$path[i]$ = $v$，表示集合$S$内顶到$v$到集合外顶点$i$的当前距离最近。
    
    

代码实现：

void Dijkatra(MGraph &G, int u, int dist[], int path[])
    int S[maxvertexnum]; //S为已求最短路径的顶点集合
    for(int i=0; i<G.vexnum; i++)S[i]=0; //集合初始化
    S[u] = 1; //起始点进集合
    for(int i=0; i<G.vexnum; i++) //dist与path数组初始化
        dist[i] = G.Edge[u][i]; //表示源点u到顶点i的最短距离
        if(u!=i && dist[i]<maxweight) //源点u到i有路径
            path[i] = u; //i的前驱结点为u
        else
            path[i] = -1; //否则i没有前驱结点
    
    for(int i=0; i<G.vexnum; i++) //对所有的顶点处理一次
        if(i != u) //排除源点
            int min = maxweight; //选不属于S且具有最短路径的顶点v
            int v = u;
            for(int j=0; j<G.vexnum; j++)
                if(!S[j] && dist[j]<min) //找最短路径，就是找dist[i]的最小值
                    v = j; //取最小值的顶点下标
                    min = dist[j]; //最小值
                
            
            S[v] = 1; //将顶点v加入集合
            for(int j=0; j<G.vexnum; j++)
            	//如果源点到顶点j的距离 > 源点经过顶点v再到达j的距离
                if(!S[j] && dist[j] > dist[v]+G.Edge[v][j]) 
                    dist[j] = G.Edge[v][j] + dist[v]; //更新最小距离和前驱结点
                    path[j] = v; //j的前驱结点为v
                
            
        
    

输出最短路径及路径长度

void PrintPath(MGraph &G, int u, int dist[], int path[])
    cout<<"各顶点到顶点"<<u<<"的最短路径为："<<endl;
    for(int i=0; i<G.vexnum; i++)
        int j=i;
        while(j!=u)
            cout<<G.Vertex[j]<<" ";
            if(j!=u) j=path[j];
        
        cout<<G.Vertex[j]<<"   dist="<<dist[i]<<endl;
    

对于下图，运行结果为：

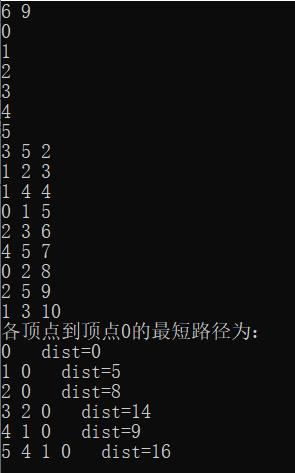
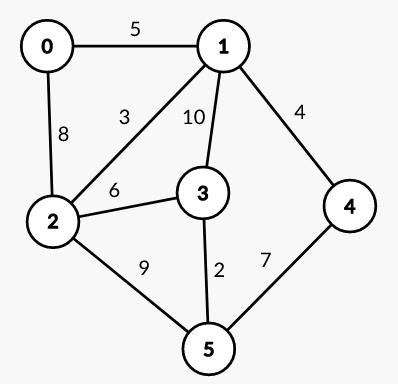
需要注意的是，边上带有负权值时，Dijkstra算法并不适用。

---

求各个顶点之间最短路径的Floyd算法

Floyd算法用于求所有顶点之间的最短路径。
求所有顶点之间的最短路径问题的提法是：已知一个带权有向图，对每一对顶点$v_i\ne v_j$，要求求出$v_i$与$v_j$之间的最短路径和最短路径长度。

Floyd算法的基本思想：
设置一个$n\times n$的方阵$A^{(k)}$，其中除对角线的元素都等于0外，其他元素$a^{(k)}[i][j]（i\ne j）$表示从顶点$v_i$到顶点$v_j$的路径长度，$k$表示绕行第$k$个顶点的运算步骤。

算法步骤：
<1>初始时，对于任意两个顶点$v_i$和$v_j$，若它们之间存在边，则以此边上的权值作为它们之间的最短路径长度；若它们之间不存在有向边，则以maxweight（机器可表示的在问题中不会遇到的最大数，表示∞）作为它们之间的最短路径长度。
<2>以后逐步尝试在原路径上加入顶点$k(k=0,1,\dots$

图的最短路径-----------Dijkstra算法详解（TjuOj2870_The Kth City）

参赛博文 | 求图的最短路径---四种算法优化

最短路径算法整理

Dijkstra算法——计算一个点到其他所有点的最短路径的算法

【数据结构】最短路径之迪杰斯特拉(Dijkstra)算法与弗洛伊德(Floyd)算法