“玲珑杯”ACM比赛 Round #19题解&源码A,规律,B,二分,C,牛顿迭代法,D,平衡树,E,概率dp
Posted Angel_Kitty
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了“玲珑杯”ACM比赛 Round #19题解&源码A,规律,B,二分,C,牛顿迭代法,D,平衡树,E,概率dp相关的知识,希望对你有一定的参考价值。
A -- simple math problem
Time Limit:2s Memory Limit:128MByte
Submissions:1599Solved:270
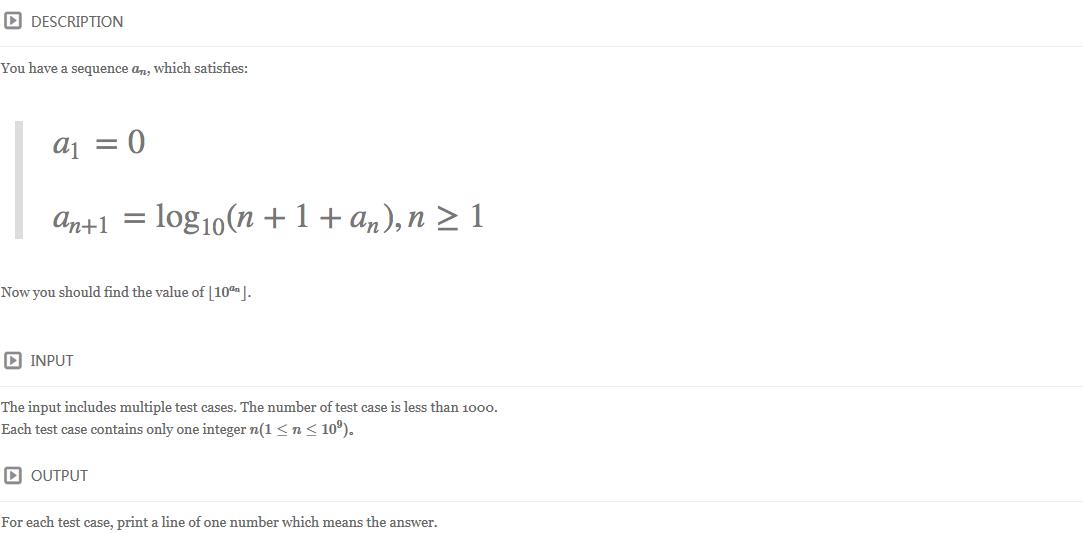

这个题解是官方写法,官方代码如下:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 typedef long long ll; 7 const int mo=1e9+7; 8 int pow(int a,int b,int c){int ret=1;for(;b;b>>=1,a=1LL*a*a%c)if(b&1)ret=1LL*ret*a%c;return ret;} 9 10 int p[10], q[10]; 11 12 int work(int n){ 13 int t = 0; 14 for(int i = 0;i <= 9;i ++) if(n >= q[i]) t = i; 15 return n + t; 16 } 17 18 int gr(){ 19 return (rand() << 16) + rand(); 20 } 21 22 int main(){ 23 p[0] = 1; 24 int t = 1; 25 for(int i = 1;i <= 9;i ++) p[i] = p[i - 1] * 10, q[i] = p[i] + 2 - i; 26 int n; 27 while(scanf("%d", &n) != EOF) printf("%d\\n", work(n)); 28 return 0; 29 }
这题我Wa了八发过了,和官方解法不同,怎么做呢?
一看就觉得肯定是规律题吧,打个表先?于是确实发现了一波规律,结论如下:
输入的这个数如果小于等于10,输出这个数
否则输入这个数加(位数减1)>=pow(10,t),其中t表示这个数的位数,大于输出结果为这个数+位数,否则输出这个数+(位数-1)
下面给出AC代码:(多组输入)
1 #include <bits/stdc++.h> 2 using namespace std; 3 int n; 4 int main() 5 { 6 while(cin>>n) 7 { 8 if(n>=0&&n<=10) 9 cout<<n<<endl; 10 else 11 { 12 int ans=0,t=0; 13 int m=n; 14 while(m) 15 { 16 m/=10; 17 t++; 18 } 19 if((n+t-1)>pow(10,t)) 20 cout<<n+t<<endl; 21 else 22 cout<<n+t-1<<endl; 23 } 24 } 25 return 0; 26 }
B -- Buildings
Time Limit:2s Memory Limit:128MByte
Submissions:682Solved:178
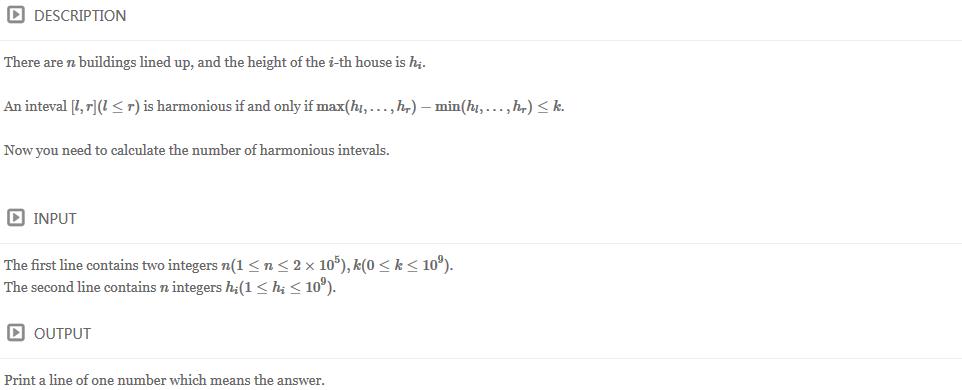
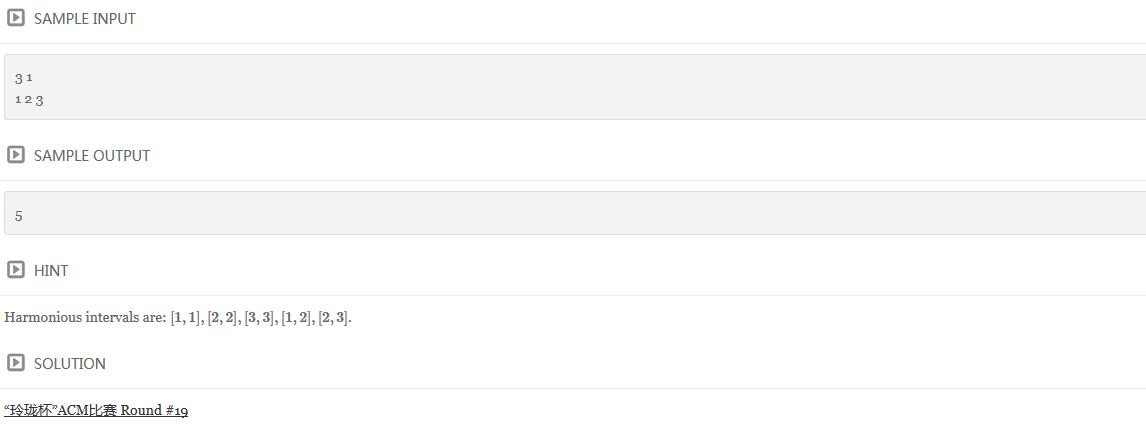
题目链接:http://www.ifrog.cc/acm/problem/1149
分析:

下面给出AC代码:
1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <algorithm> 5 using namespace std; 6 7 #define N 200010 8 9 int n, K, a[N], lg[N], f[20][N], g[20][N]; 10 11 int ask(int l, int r){ 12 int k = lg[r - l + 1]; 13 return max(f[k][l], f[k][r - (1 << k) + 1]) - min(g[k][l], g[k][r - (1 << k) + 1]); 14 } 15 16 int main(){ 17 // freopen("1.in", "r", stdin); 18 scanf("%d%d", &n, &K); 19 for(int i = 2;i <= n;i ++) if(i & (i - 1)) lg[i] = lg[i - 1]; else lg[i] = lg[i - 1] + 1; 20 for(int i = 1;i <= n;i ++) scanf("%d", &a[i]), f[0][i] = g[0][i] = a[i]; 21 for(int i = 1;(1 << i) <= n;i ++){ 22 for(int j = 1;j + (1 << i) - 1 <= n;j ++){ 23 f[i][j] = max(f[i - 1][j], f[i - 1][j + (1 << (i - 1))]); 24 g[i][j] = min(g[i - 1][j], g[i - 1][j + (1 << (i - 1))]); 25 } 26 } 27 long long ans = 0; 28 for(int i = 1;i <= n;i ++){ 29 int l = i, r = n, mid; 30 while(l <= r){ 31 mid = (l + r) >> 1; 32 if(ask(i, mid) <= K) l = mid + 1; else r = mid - 1; 33 } 34 ans += l - i; 35 } 36 cout << ans << endl; 37 return 0; 38 }
C -- Collecting apples
Time Limit:2s Memory Limit:128MByte
Submissions:24Solved:7
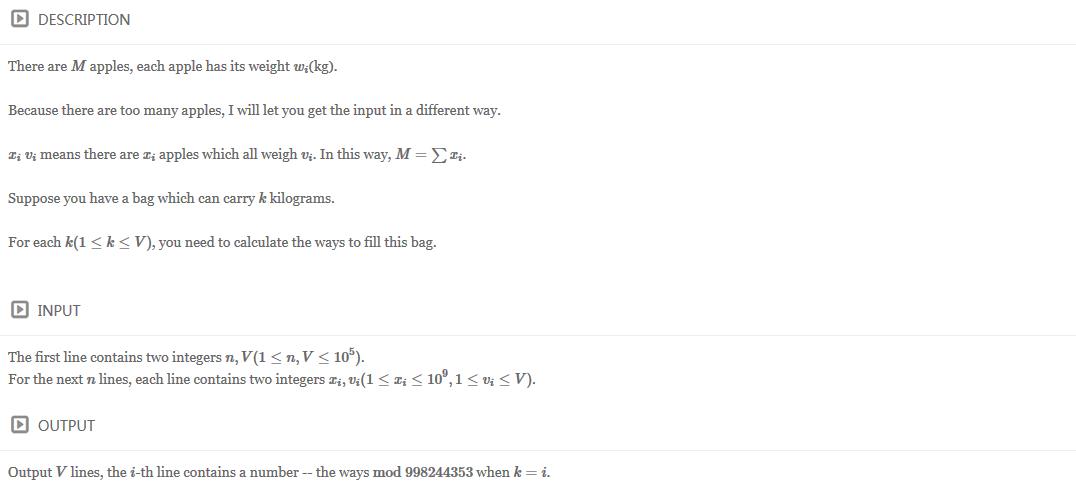
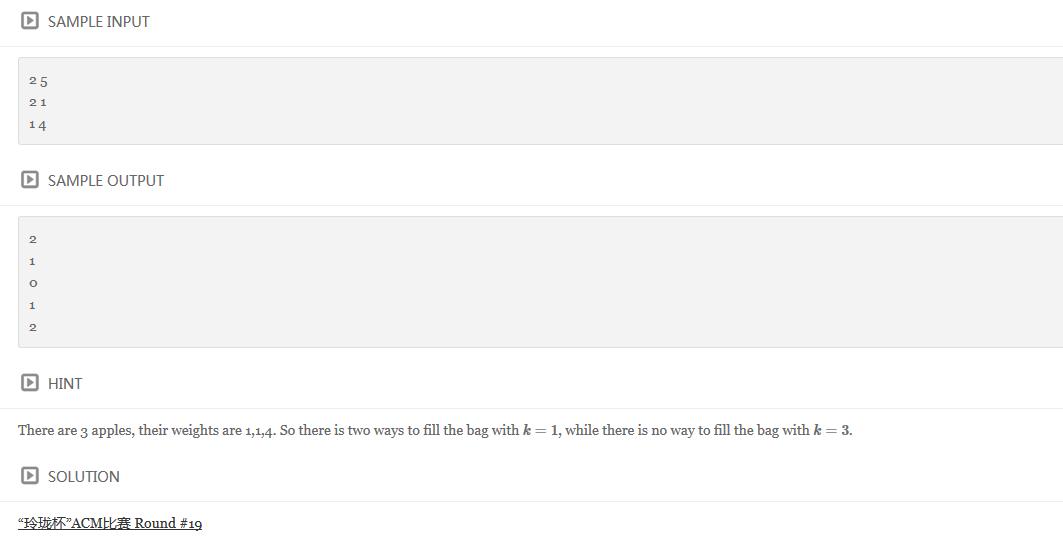
题目链接:http://www.ifrog.cc/acm/problem/1150
分析:

下面给出AC代码:
1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <algorithm> 5 using namespace std; 6 7 typedef int value_t; 8 typedef long long calc_t; 9 const int MaxN = 1 << 19; 10 const value_t mod_base = 119, mod_exp = 23; 11 const value_t mod_v = (mod_base << mod_exp) + 1; 12 const value_t primitive_root = 3; 13 int epsilon_num; 14 value_t eps[MaxN], inv_eps[MaxN], inv2, inv[MaxN]; 15 16 value_t dec(value_t x, value_t v) { x -= v; return x < 0 ? x + mod_v : x; } 17 value_t inc(value_t x, value_t v) { x += v; return x >= mod_v ? x - mod_v : x; } 18 value_t pow(value_t x, value_t p){ 19 value_t v = 1; 20 for(; p; p >>= 1, x = (calc_t)x * x % mod_v) 21 if(p & 1) v = (calc_t)x * v % mod_v; 22 return v; 23 } 24 25 void init_eps(int num){ 26 epsilon_num = num; 27 value_t base = pow(primitive_root, (mod_v - 1) / num); 28 value_t inv_base = pow(base, mod_v - 2); 29 eps[0] = inv_eps[0] = inv[0] = 1; 30 for(int i = 1; i < num; ++i) 31 inv[i] = pow(i, mod_v - 2); 32 for(int i = 1; i < num; ++i){ 33 eps[i] = (calc_t)eps[i - 1] * base % mod_v; 34 inv_eps[i] = (calc_t)inv_eps[i - 1] * inv_base % mod_v; 35 } 36 } 37 38 void transform(int n, value_t *x, value_t *w = eps){ 39 for(int i = 0, j = 0; i != n; ++i){ 40 if(i > j) swap(x[i], x[j]); 41 for(int l = n >> 1; (j ^= l) < l; l >>= 1); 42 } 43 for(int i = 2; i <= n; i <<= 1){ 44 int m = i >> 1, t = epsilon_num / i; 45 for(int j = 0; j < n; j += i){ 46 for(int p = 0, q = 0; p != m; ++p, q += t){ 47 value_t z = (calc_t)x[j + m + p] * w[q] % mod_v; 48 x[j + m + p] = dec(x[j + p], z); 49 x[j + p] = inc(x[j + p], z); 50 } 51 } 52 } 53 } 54 55 void inverse_transform(int n, value_t *x){ 56 transform(n, x, inv_eps); 57 value_t inv = pow(n, mod_v - 2); 58 for(int i = 0; i != n; ++i) 59 x[i] = (calc_t)x[i] * inv % mod_v; 60 } 61 62 void polynomial_inverse(int n, value_t *A, value_t *B){ 63 static value_t T[MaxN]; 64 if(n == 1){ 65 B[0] = pow(A[0], mod_v - 2); 66 return; 67 } 68 int half = (n + 1) >> 1; 69 polynomial_inverse(half, A, B); 70 int p = 1; 71 for(; p < n << 1; p <<= 1); 72 fill(B + half, B + p, 0); 73 transform(p, B); 74 copy(A, A + n, T); 75 fill(T + n, T + p, 0); 76 transform(p, T); 77 for(int i = 0; i != p; ++i) 78 B[i] = (calc_t)B[i] * dec(2, (calc_t)T[i] * B[i] % mod_v) % mod_v; 79 inverse_transform(p, B); 80 } 81 82 void polynomial_logarithm(int n, value_t *A, value_t *B){ 83 static value_t T[MaxN]; 84 int p = 1; 85 for(; p < n << 1; p <<= 1); 86 polynomial_inverse(n, A, T); 87 fill(T + n, T + p, 0); 88 transform(p, T); 89 copy(A, A + n, B); 90 for(int i = 0; i < n - 1; ++i) 91 B[i] = (calc_t)B[i + 1] * (i + 1) % mod_v; 92 fill(B + n - 1, B + p, 0); 93 transform(p, B); 94 for(int i = 0; i != p; ++i) 95 B[i] = (calc_t)B[i] * T[i] % mod_v; 96 inverse_transform(p, B); 97 for(int i = n - 1; i; --i) 98 B[i] = (calc_t)B[i - 1] * inv[i] % mod_v; 99 B[0] = 0; 100 } 101 102 void polynomial_exponent(int n, value_t *A, value_t *B) 103 { 104 static value_t T[MaxN]; 105 if(n == 1){ 106 B[0] = 1; 107 return; 108 } 109 int p = 1; 110 for(; p < n << 1; p <<= 1); 111 int half = (n + 1) >> 1; 112 polynomial_exponent(half, A, B); 113 fill(B + half, B + p, 0); 114 polynomial_logarithm(n, B, T); 115 for(int i = 0; i != n; ++i) 116 T[i] = dec(A[i], T[i]); 117 T[0] = inc(T[0], 1); 118 transform(p, T); 119 transform(p, B); 120 for(int i = 0; i != p; ++i) 121 B[i] = (calc_t)B[i] * T[i] % mod_v; 122 inverse_transform(p, B); 123 } 124 125 value_t tmp[MaxN]; 126 value_t A[MaxN], B[MaxN], C[MaxN], T[MaxN]; 127 128 int main(){ 129 // freopen("1.in", "r", stdin); 130 // freopen("1.out", "w", stdout); 131 int n, m, nn, xx, yy; 132 scanf("%d%d", &nn, &n); 133 for(int i = 1;i <= n;i ++) tmp[i] = 0; 134 for(int i = 1;i <= nn;i ++) scanf("%d%d", &xx, &yy), tmp[yy] += xx; 135 inv2 = mod_v - mod_v / 2; 136 int p = 1; 137 for(; p < (n + 5) << 1; p <<= 1); 138 init_eps(p); 139 for(int j = 1;j <= n;j ++){ 140 for(int i = 1;i * j <= n;i ++) 141 if(j & 1) A[i * j] = (A[i * j] + 1LL * inv[j] * tmp[i]) % mod_v; 142 else A[i * j] = ((A[i * j] - 1LL * inv[j] * tmp[i]) % mod_v + mod_v) % mod_v; 143 } 144 polynomial_exponent(n + 5, A, B); 145 for(int i = 1; i <= n;i ++) printf("%d\\n", (B[i] + mod_v) % mod_v); 146 return 0; 147 }
D -- Delivering parcels
Time Limit:2s Memory Limit:128MByte
Submissions:114Solved:16
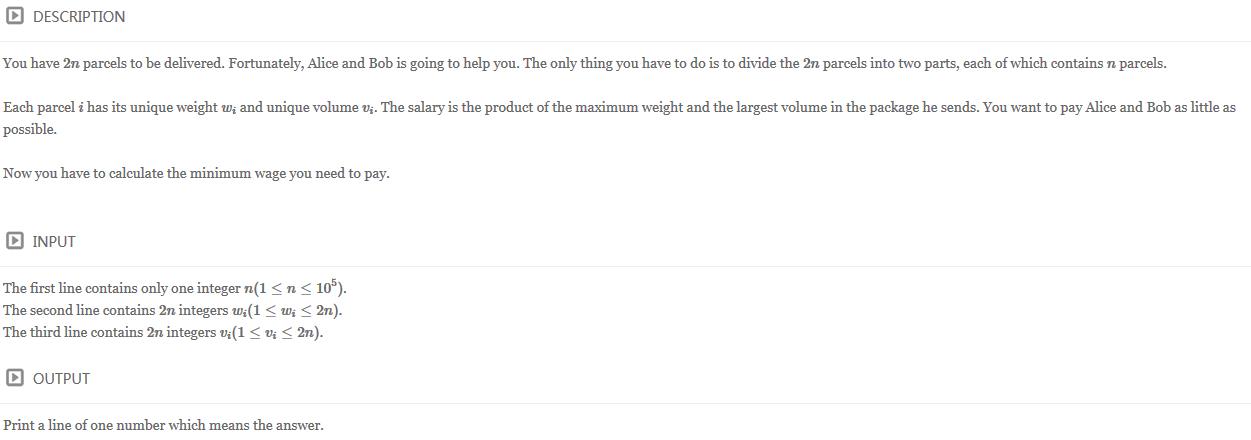
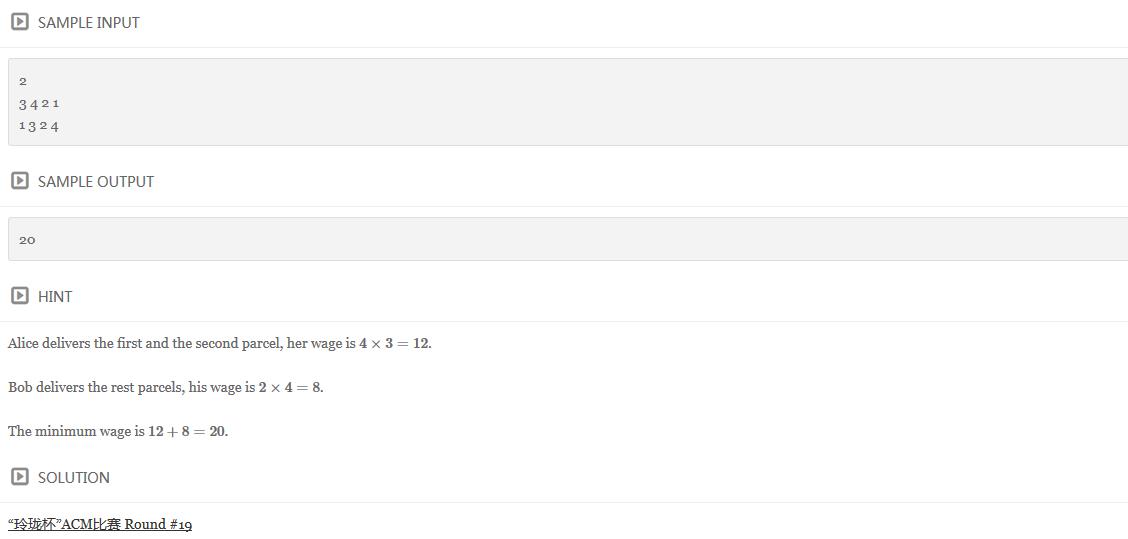
题目链接:http://www.ifrog.cc/acm/problem/1151
分析:

下面给出AC代码:
1 #include <iostream> 2 #include <stdio.h> 3 #include <math.h> 4 #include <string.h> 5 #include <time.h> 6 #include <stdlib.h> 7 #include <string> 8 #include <bitset> 9 #include <vector> 10 #include <set> 11 #include <map> 12 #include <queue> 13 #include <algorithm> 14 #include <sstream> 15 #include <stack> 16 #include <iomanip> 17 using namespace std; 18 #define pb push_back 19 #define mp make_pair 20 typedef pair<int,int> pii; 21 typedef long long ll; 22 typedef double ld; 23 typedef vector<int> vi; 24 #define fi first 25 #define se second 26 #define fe first 27 #define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);} 28 #define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);} 29 #define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);} 30 #define es(x,e) (int e=fst[x];e;e=nxt[e]) 31 #define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e]) 32 #define VIZ {printf("digraph G{\\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\\n",i,vb[e]); puts("}");} 33 #define VIZ2 {printf("graph G{\\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\\n",i,vb[e]); puts("}");} 34 #define SZ 666666 35 int n,w[SZ],v[SZ]; 36 ll ans=1e18; 37 pii ps[SZ]; 38 int hm[SZ]; 39 #include <ext/pb_ds/tree_policy.hpp> 40 #include <ext/pb_ds/assoc_container.hpp> 41 using namespace __gnu_pbds; 42 typedef tree<int,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update> rbtt; 43 rbtt rbt; 44 void case1(int A,int B) 45 { 46 rbt.clear(); 47 int r=n-1,g=0; 48 for(int i=1;i<=n+n;++i) 49 if(i!=A&&i!=B) ps[++g]=pii(w[i],v[i]); 50 sort(ps+1,ps+1+g); hm[g+1]=-1e9; 51 for(int i=g;i>=1;--i) 52 hm[i]=max(hm[i+1],ps[i].se); 53 for(int i=1;i<=g;++i) 54 { 55 rbt.insert(ps[i].se); 56 if(g-i>r) continue; 57 int cur=hm[i+1],rm=r-(g-i); 58 if(rm) cur=max(cur,*rbt.find_by_order(rm-1)); 59 ans=min(ans,(ll)max(w[B],ps[i].fi)*v[B]+(ll)w[A]*max(cur,v[A])); 60 } 61 } 62 void case2(int A,int B) 63 { 64 rbt.clear(); 65 int g=0; 66 for(int i=1;i<=n+n;++i) 67 if(i!=A&&i!=B) ps[++g]=pii(w[i],v[i]); 68 sort(ps+1,ps+1+g); 69 int pp=0,p2=0; 70 for(int i=1;i<=g;++i) 71 { 72 rbt.insert(ps[i].se); 73 if(rbt.size()<n) continue; 74 int cur=*rbt.find_by_order(n-1); 75 ans=min(ans,(ll)w[A]*v[B]+(ll)ps[i].fi*cur); 76 } 77 } 78 int main() 79 { 80 scanf("%d",&n); 81 for(int i=1;i<=n+n;++i) 82 scanf("%d",w+i); 83 for(int i=1;i<=n+n;++i) 84 scanf("%d",v+i); 85 if(n==1) 86 { 87 printf("%lld\\n",w[1]*(ll)v[1]+w[2]*(ll)v[2]); 88 return 0; 89 } 90 pii m1(-1e9,-1e9),m2(-1e9,-1e9); 91 for(int i=1;i<=n+n;++i) 92 m1=max(m1,pii(w[i],i)), 93 m2=max(m2,pii(v[i],i)); 94 int A=m1.se,B=m2.se; 95 if以上是关于“玲珑杯”ACM比赛 Round #19题解&源码A,规律,B,二分,C,牛顿迭代法,D,平衡树,E,概率dp的主要内容,如果未能解决你的问题,请参考以下文章“玲珑杯”ACM比赛 Round #19 B -- Buildings (RMQ + 二分)
“玲珑杯”ACM比赛 Round #19 B -- Buildings
“玲珑杯”ACM比赛 Round #18 图论你先敲完模板(dp)