城市来往最短路线

Posted 2020-09-29 寄蜉蝣于天地，渺沧海之一粟

书里面的一道题，记录一下代码。

原题大概是这么个样子：如下图所示表示的是从城市A到城市H的交通图。从图中可以看出，从城市A到城市H要经过若干个城市。现要找出一条经过城市最少的一条路线。

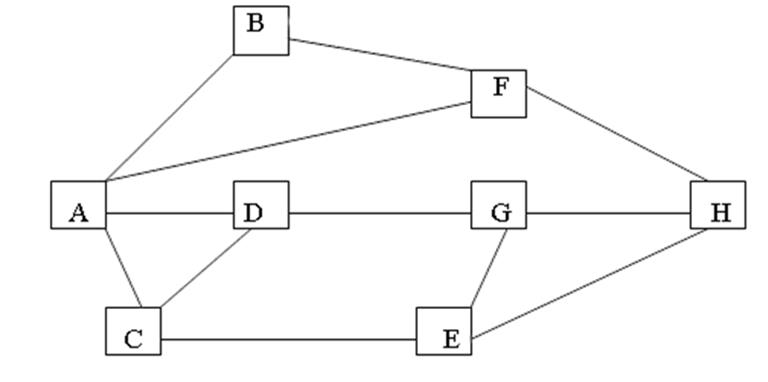
【算法分析】

看到这图很容易想到用邻接距阵来存储图中各节点的边的关系，1表示能走，0表示不能走。

首先想到的是用队列的思想。a数组是存储扩展结点的队列，a[i]记录经过的城市,b[i]记录前趋城市，这样就可以倒推出最短线路。具体过程如下：

（1） 将城市A入队，队首为0、队尾为1。

（2）将队首所指的城市所有可直通的城市入队（如果这个城市在队列中出现过就不入队，可用一布尔数组s[i]来判断），将入队城市的前趋城市保存在b[i]中。然后将队首加1，得到新的队首城市。重复以上步骤，直到搜到城市H时，搜索结束。利用b[i]可倒推出最少城市线路。

下面稍微细化一下题设：

输入n和e表示有n个城市，城市之间的连线有e条。然后输入e行，每行两个整数x和y表示城市x和y之间有边链接。

接着输入s和d表示出发点和目的点。

输出从s到d之间的最短路径（边的数量最少）以及路径长度 。

用于测试的输入数据：

8 12
A B
A F
A D
A C
B F
C D
C E
D G
E G
E H
F H
G H
A H

代码：

 1 #include <stdio.h>
 2 
 3 #define maxN 1005
 4 #define maxE 5005
 5 
 6 struct obj
 7 {
 8     int no,pre;
 9 };
10 
11 int n,e;//无向图的n个顶点，e条边(顶点编号：1~n)
12 int p[maxN][maxN]={0};//邻接矩阵，无向图中各条边的数据   
13 int begin,end;//出发点、终止点
14 struct obj a[maxN];//BFS队列
15 int head,tril;//队列的头、尾
16 int check[maxN]={0};//check[i]==0表示第i个顶点未曾入队
17 int flag=-1;//尚未搜索到终止点
18 
19 void BFS();
20 void print();
21 
22 int main(int argc, char *argv[])
23 {
24     //freopen("data.txt","r",stdin);
25     int i,x,y;
26     char xx,yy;
27     scanf("%d%d",&n,&e);getchar();
28     for(i=0;i<e;i++)
29     {
30         scanf("%c %c",&xx,&yy);getchar();
31         x=xx-\'A\'+1;  y=yy-\'A\'+1;
32         p[x-1][y-1]=1;
33         p[y-1][x-1]=1;
34     }
35     scanf("%c %c",&xx,&yy);
36     begin=xx-\'A\'+1;  end=yy-\'A\'+1;
37     begin--;
38     end--;
39     BFS();
40     if(flag==1) print();
41     else printf("no answer!\\n");
42     return 0;
43 }
44 void BFS()
45 {
46     struct obj temp;
47     int j;
48     head=0;//初始化队列
49     tril=0;//初始化队列
50 
51     a[tril].no=begin;//出发点入队
52     a[tril].pre=-1;//出发点不考虑前驱节点
53     check[begin]=1;//标记出发点已经入队
54 
55     if(begin==end)
56     {
57         flag=1;
58         return ;//出发点和终止点相同，可以直接返回了。
59     }
60 
61     while(tril-head+1>0)//当队列不为空时继续搜过
62     {
63         temp=a[head];
64          for(j=0;j<maxN;j++)//寻找temp节点的相邻节点，把相邻节点入队
65         {
66             if(p[temp.no][j]==1&&check[j]==0)//发现相邻节点j而且相邻节点j尚未入过队
67             {
68                 tril++;
69                 a[tril].no=j;//相邻节点j入队
70                 a[tril].pre=head;//相邻节点j的上一个节点(也就是temp节点)在队列当中的下标
71                 check[j]=1;
72                 if(j==end)
73                 {
74                     flag=1;//已经找到了终点end
75                     break;
76                 }
77             }
78         }
79         head++;//队头出队
80         if(flag==1)
81         {
82             break;
83         }
84     }
85 }
86 void print()
87 {
88     int i;
89     for(i=tril;i>=0;)
90     {
91         //printf("%d ",a[i].no+1);//输出节点编号（编号1~n）
92         printf("%c ",a[i].no+\'A\'); 
93         i=a[i].pre;
94     }
95     printf("\\n");
96 }

样例代码2：

  1 #include<stdio.h>
  2 #include<queue>
  3 #include<iostream>
  4 using namespace std;
  5 
  6 #define maxN 1005
  7 #define maxE 5005
  8 
  9 struct obj
 10 {
 11     int no,pre;
 12 };
 13 
 14 int n,e;//无向图的n个顶点，e条边(顶点编号：1~n)
 15 int p[maxN][maxN]={0};//邻接矩阵，无向图中各条边的数据   
 16 int begin,end;//出发点、终止点
 17 queue<obj> q;//BFS队列
 18 int s[maxN]={0};//用于记录出发点到目的点的路径。s[i]=k表节点i的前驱是节点k。 
 19 int check[maxN]={0};//check[i]==0表示第i个顶点未曾入队
 20 int flag=-1;//尚未搜索到终止点
 21 
 22 void BFS();
 23 void print();
 24 
 25 int main()
 26 {
 27     freopen("data.txt","r",stdin);
 28     int i,x,y;
 29     char xx,yy;
 30     scanf("%d%d",&n,&e);getchar();
 31     for(i=0;i<e;i++)
 32     {
 33         scanf("%c %c",&xx,&yy);getchar();
 34         /*x=xx-\'A\'+1;  y=yy-\'A\'+1;
 35         p[x-1][y-1]=1;
 36         p[y-1][x-1]=1;*/
 37         x=xx-\'A\'; y=yy-\'A\';
 38         p[x][y]=1;
 39         p[y][x]=1;
 40     }
 41     scanf("%c %c",&xx,&yy);
 42     /*begin=xx-\'A\'+1;  end=yy-\'A\'+1;
 43     begin--;
 44     end--;*/
 45     begin=xx-\'A\';  end=yy-\'A\';
 46     
 47     BFS();
 48     if(flag==1) print();
 49     else printf("no answer!\\n");
 50     return 0;
 51 }
 52 void BFS()
 53 {
 54     struct obj temp,temp2;
 55     int j;
 56 
 57     temp.no=begin;//出发点入队
 58     temp.pre=-1;//出发点不考虑前驱节点
 59     q.push(temp);
 60     check[begin]=1;//标记出发点已经入队
 61     s[begin]=-1;
 62     
 63     if(begin==end)
 64     {
 65         flag=1;
 66         return ;//出发点和终止点相同，可以直接返回了。
 67     }
 68 
 69     while(!q.empty())//当队列不为空时继续搜过
 70     {
 71         temp=q.front();
 72          for(j=0;j<maxN;j++)//寻找temp节点的相邻节点，把相邻节点入队
 73         {
 74             if(p[temp.no][j]==1&&check[j]==0)//发现相邻节点j而且相邻节点j尚未入过队
 75             {
 76                 temp2.no=j;
 77                 temp2.pre=temp.no;
 78                 q.push(temp2);
 79                 check[j]=1;
 80                 s[j]=temp.no;
 81                 
 82                 if(j==end)
 83                 {
 84                     flag=1;//已经找到了终点end
 85                     break;
 86                 }
 87             }
 88         }
 89         q.pop();//队头出队
 90         if(flag==1)
 91         {
 92             break;
 93         }
 94     }
 95 }
 96 void print()
 97 {
 98     int i;
 99     printf("%c ",end+\'A\');
100     for(i=end;i!=begin;)
101     {
102         //printf("%d ",a[i].no+1);//输出节点编号（编号1~n）
103         printf("%c ",s[i]+\'A\'); 
104         i=s[i];
105     }
106     printf("\\n");
107 }