基本模型之图论篇

Posted 2020-11-02 miracle-z

最短路径问题

（给定连接若干城市的公路网，寻找从指定城市到各城市去的最短路线。）

涉及算法：

　　1.贪心算法（由局部最优解求全局最优解）

　　　　贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。

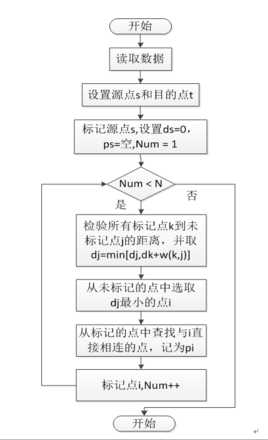
　　2.Kijkstra算法

　　　　迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。

 

最小生成树问题

最小生成树概念：现在假设有一个很实际的问题：我们要在n个城市中建立一个通信网络，则连通这n个城市需要布置n-1一条通信线路，这个时候我们需要考虑如何在成本最低的情况下建立这个通信网？
于是我们就可以引入连通图来解决我们遇到的问题，n个城市就是图上的n个顶点，然后，边表示两个城市的通信线路，每条边上的权重就是我们搭建这条线路所需要的成本，所以现在我们有n个顶点的连通网可以建立不同的生成树，每一颗生成树都可以作为一个通信网，当我们构造这个连通网所花的成本最小时，搭建该连通网的生成树，就称为最小生成树。

　　构成生成树的准则有三条：
　　<1> 必须只使用该网络中的边来构造最小生成树。
　　<2> 必须使用且仅使用n-1条边来连接网络中的n个顶点
　　<3> 不能使用产生回路的边

涉及算法：

　　Kruskal算法：

　　克鲁斯卡尔算法的基本思想是以边为主导地位，始终选择当前可用（所选的边不能构成回路）的最小权植边。所以Kruskal算法的第一步是给所有的边按照从小到大的顺序排序。

　　具体实现过程如下

　　<1>　设一个有n个顶点的连通网络为G（V,E），最初先构造一个只有n个顶点，没有边的非连通图T={V,空}，图中每个顶点自成一格连通分量。

 

　　<2>　在Ｅ中选择一条具有最小权植的边时，若该边的两个顶点落在不同的连通分量上，则将此边加入到Ｔ中；否则，即这条边的两个顶点落到同一连通分量      上，则将此边舍去　　（此后永不选用这条边），重新选择一条权植最小的边。

 

　　<3>　如此重复下去，直到所有顶点在同一连通分量上为止。

 

中国邮路问题

涉及算法：

　　　　Edmons-Johnson算法

人员安排问题

涉及算法：

　　匈牙利算法（二分图分配）　

　　由增广路的性质，增广路中的匹配边总是比未匹配边多一条，所以如果我们放弃一条增广路中的匹配边，选取未匹配边作为匹配边，则匹配的数量就会增加。匈牙利算法就是在不断寻找增广路，如果找不到增广　　路，就说明达到了最大匹配。

　　举个例子 
　　1、起始没有匹配 

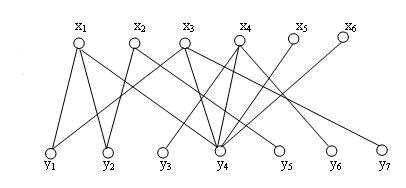
　　2、选中第一个x点找第一跟连线 

 

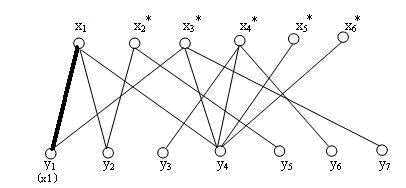
　　3、选中第二个点找第二跟连线 

 

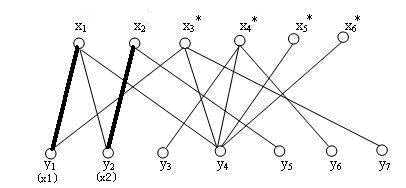
　　4、发现x3的第一条边x3y1已经被人占了，找出x3出发的的交错路径x3-y1-x1-y4，把交错路中已在匹配上的边x1y1从匹配中去掉，剩余的边x3y1 x1y4加到匹配中去 

 

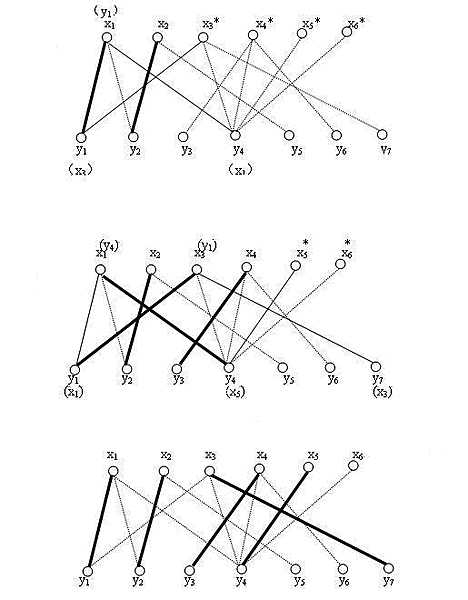
　　5、同理加入x4,x5。 

　　匈牙利算法可以深度有限或者广度优先，刚才的示例是深度优先，即x3找y1,y1已经有匹配，则找交错路。若是广度优先，应为：x3找y1,y1有匹配，x3找y2。

　　　

最大流问题

涉及算法：

　　Ford-Fulkerson算法

　　

　　最大流问题常常出现在物流配送中，可以规约为以下的图问题。最大流问题中，图中两个顶点之间不能同时存在一对相反方向的边。

　　边上的数字为该条边的容量，即在该条边上流过的量的上限值。最大流问题就是在满足容量限制条件下，使从起点s到终点t的流量达到最大。在介绍解决最大流问题的Ford-Fulkerson方法之前，先介绍一些基本　　概念。

　　1.  残存网络与增广路径

　　根据图和各条边上的流可以画出一幅图的残存网络如下所示。左图为流网络，右图为残存网络，其中流网络中边上的数字分别是流量和容量，如10/12，那么10为边上的流量，12为边的容量。残存网络中可能会　　存在一对相反方向的边，与流网络中相同的边代表的是流网络中该边的剩余容量，在流网络中不存在的边代表的则是其在流网络中反向边的已有流量，这部分流量可以通过“回流”减少。例如，右图残存网络中，　　边<s,v1>的剩余容量为4，其反向边<v1.s>的值为12，即左图流网络中的边<s,v1>的流量。在残存网络中，值为0的边不会画出，如边<v1,v2>。

　　残存网络描述了图中各边的剩余容量以及可以通过“回流”删除的流量大小。在Ford-Fulkerson方法中，正是通过在残存网络中寻找一条从s到t的增广路径，并对应这条路径上的各边对流网络中的各边的流进行修　　改。如果路径上的一条边存在于流网络中，那么对该边的流增加，否则对其反向边的流减少。增加或减少的值是确定的，就是该增广路径上值最小的边

　　

旅行推销员问题

涉及算法：

　　遗传算法

　　遗传算法是解决搜索问题的一种通用算法，对于各种通用问题都可以使用。搜索算法的共同特征为：
　　① 首先组成一组候选解
　　② 依据某些适应性条件测算这些候选解的适应度
　　③ 根据适应度保留某些候选解，放弃其他候选解
　　④ 对保留的候选解进行某些操作，生成新的候选解。