归并排序（Merge Sort）

Posted 2020-06-25 |瑾诺学长|

 

基本思想：

归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

归并排序示例：

 

 

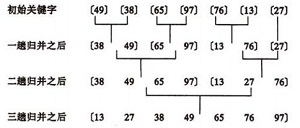
合并方法：

若i>m 或j>n，转⑷ //其中一个子表已合并完，比较选取结束

• //选取r[i]和r[j]较小的存入辅助数组rf
  如果r[i]<r[j]，rf[k]=r[i]； i++； k++； 转⑵
  否则，rf[k]=r[j]； j++； k++； 转⑵
• //将尚未处理完的子表中元素存入rf
  如果i<=m，将r[i…m]存入rf[k…n] //前一子表非空
  如果j<=n ,  将r[j…n] 存入rf[k…n] //后一子表非空
• 合并结束。

 

//将r[i…m]和r[m +1 …n]归并到辅助数组rf[i…n]
void Merge(ElemType *r,ElemType *rf, int i, int m, int n)
{
	int j,k;
	for(j=m+1,k=i; i<=m && j <=n ; ++k){
		if(r[j] < r[i]) rf[k] = r[j++];
		else rf[k] = r[i++];
	}
	while(i <= m)  rf[k++] = r[i++];
	while(j <= n)  rf[k++] = r[j++];
}

 

归并的迭代算法

 

1 个元素的表总是有序的。所以对n 个元素的待排序列，每个元素可看成1 个有序子表。对子表两两合并生成n/2个子表，所得子表除最后一个子表长度可能为1 外，其余子表长度均为2。再进行两两合并，直到生成n 个元素按关键码有序的表。

 

void print(int a[], int n){
	for(int j= 0; j<n; j++){
		cout<<a[j] <<"  ";
	}
	cout<<endl;
}

//将r[i…m]和r[m +1 …n]归并到辅助数组rf[i…n]
void Merge(ElemType *r,ElemType *rf, int i, int m, int n)
{
	int j,k;
	for(j=m+1,k=i; i<=m && j <=n ; ++k){
		if(r[j] < r[i]) rf[k] = r[j++];
		else rf[k] = r[i++];
	}
	while(i <= m)  rf[k++] = r[i++];
	while(j <= n)  rf[k++] = r[j++];
	print(rf,n+1);
}

void MergeSort(ElemType *r, ElemType *rf, int lenght)
{ 
	int len = 1;
	ElemType *q = r ;
	ElemType *tmp ;
	while(len < lenght) {
		int s = len;
		len = 2 * s ;
		int i = 0;
		while(i+ len <lenght){
			Merge(q, rf,  i, i+ s-1, i+ len-1 ); //对等长的两个子表合并
			i = i+ len;
		}
		if(i + s < lenght){
			Merge(q, rf,  i, i+ s -1, lenght -1); //对不等长的两个子表合并
		}
		tmp = q; q = rf; rf = tmp; //交换q,rf，以保证下一趟归并时，仍从q 归并到rf
	}
}


int main(){
	int a[10] = {3,1,5,7,2,4,9,6,10,8};
	int b[10];
	MergeSort(a, b, 10);
	print(b,10);
	cout<<"结果：";
	print(a,10);

}
两路归并的递归算法

void MSort(ElemType *r, ElemType *rf,int s, int t)  
2.{   
3.    ElemType *rf2;  
4.    if(s==t) r[s] = rf[s];  
5.    else  
6.    {   
7.        int m=(s+t)/2;          /*平分*p 表*/  
8.        MSort(r, rf2, s, m);        /*递归地将p[s…m]归并为有序的p2[s…m]*/  
9.        MSort(r, rf2, m+1, t);      /*递归地将p[m+1…t]归并为有序的p2[m+1…t]*/  
10.        Merge(rf2, rf, s, m+1,t);   /*将p2[s…m]和p2[m+1…t]归并到p1[s…t]*/  
11.    }  
12.}  
13.void MergeSort_recursive(ElemType *r, ElemType *rf, int n)  
14.{   /*对顺序表*p 作归并排序*/  
15.    MSort(r, rf,0, n-1);  
16.}