归并排序（Merge Sort）思想，代码实现

Posted 2021-09-22 有裂痕的石头

归并排序是分治算法一个非常典型的例子，归并排序的思想是将待排序序列递归分为左右两个子序列，递归到子序列只有一个数的时候，停下来，这就是分治算法的分的意思，将问题化简，当子序列只有一个元素的时候是不是可以认为这个序列为有序序列了，然后再将左右有序子序列通过递归合并起来，最终让整个序列有序，这是分治算法治的过程，下面我们通过图片来理解这个过程：

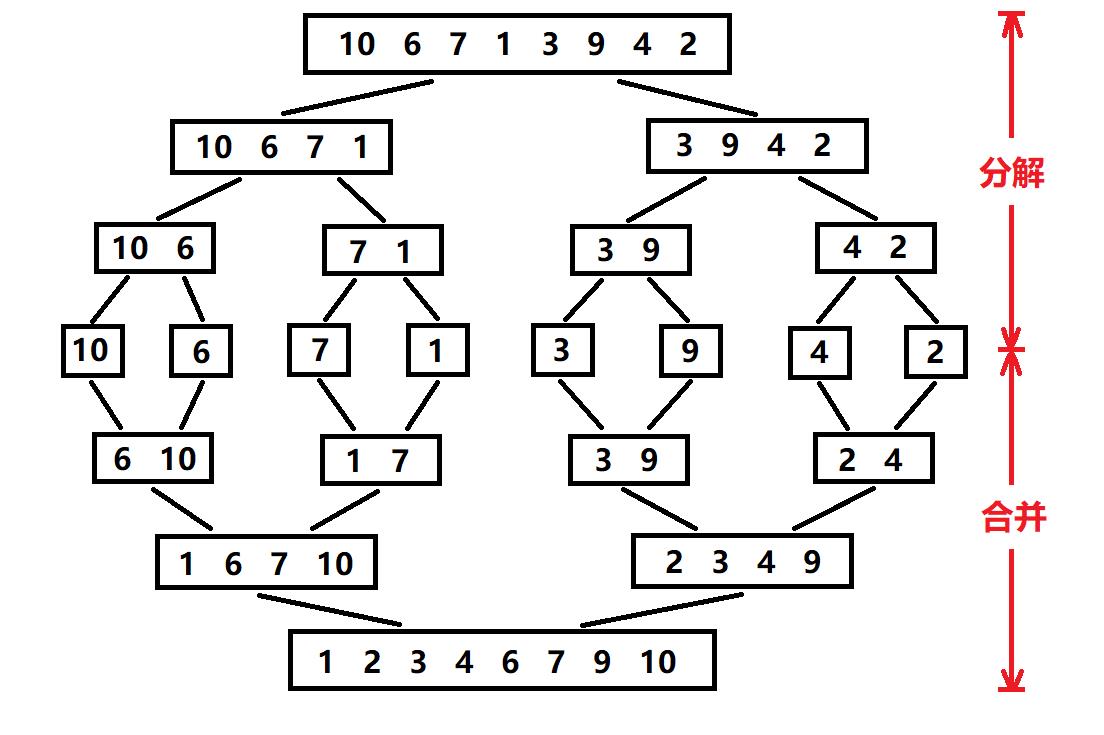
通过动图理解就是：

下面看代码：

public class MergeSort {
    public static void mergeSort(long[] array) {
        mergeSortRange(array, 0, array.length);
    }

    // [from, to)
    private static void mergeSortRange(long[] array, int from, int to) {
        int size = to - from;
        if (size <= 1) {
            return;
        }

        //int mid = (from + to) / 2;
        int mid = from + (to - from) / 2;
        // 左半边: [from, mid)
        // 右半边: [mid, to)

        // 先让左右区间各自有序
        mergeSortRange(array, from, mid);
        mergeSortRange(array, mid, to);

        // 合并两个有序区间 [from, mid) [mid, to)
        merge(array, from, mid, to);
    }

    private static void merge(long[] array, int from, int mid, int to) {
        // 需要额外空间，需要两个区间的大小之和
        int size = to - from;
        long[] array2 = new long[size];

        int k1 = from;  // array
        int k2 = mid;   // array
        int k3 = 0;     // array2

        while (k1 < mid && k2 < to) {
            if (array[k1] <= array[k2]) {   // 加等号是为了保证稳定性
                array2[k3++] = array[k1++];
            } else {
                array2[k3++] = array[k2++];
            }
        }

        // 有一个区间内的元素全部取完了
        if (k1 < mid) {
            // 左边区间还有元素
            while (k1 < mid) {
                array2[k3++] = array[k1++];
            }
        } else {
            // 右边区间还有元素
            while (k2 < to) {
                array2[k3++] = array[k2++];
            }
        }

        // 我们还需要把数据搬回原数组中
        for (int i = 0; i < size; i++) {
            array[from + i] = array2[i];
        }
    }
}

归并排序的说简单也很简单，说难他不好理解的点就是将待排序序列一直分解到只含一个数据的子序列然后在依次合并这个递归操作上。