深度优先算法--判断迷宫的一个起点能否到达一个终点
Posted byerHu
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度优先算法--判断迷宫的一个起点能否到达一个终点相关的知识,希望对你有一定的参考价值。
题目描述:
小老鼠Jerry生活在一个庞大的迷宫里,每天靠吃奶酪填饱自己的肚子。一天,它发现自己辛辛苦苦攒积的奶酪不见了。于是在迷宫里开始它的搜寻计划。迷宫是一个N*M(N,M均不超过20)的棋盘,如下图所示:
########
#.####.#
#..#..C#
#.M#..##
#..#..##
#.##...#
#......#
########
其中,“#”表示为一堵墙,Jerry是不能呆在上面的;“.”表示为空地,Jerry可以在上面任意经过,可以自由的向上下左右四个方向行走; “M”表示Jerry开始所在的位置,“C”表示奶酪所在的位置。
你的任务是:在输入中给你迷宫的描述,请问JERRY是否能找回它的奶酪?(也就是JERRY不穿过墙,只在空地上行走,是否存在一条从开始位置到奶酪所在位置的一条道路)。
输入格式:
每个输入文件有多组数据,以0 0作为结束符。每组数据第一行为N和M表示,迷宫有N行M列。接下来N行,每行M个字符描述着迷宫的形状。
输出格式:
对于每组数据,如果JERRY能找到奶酪,就输出“^_^”,否则输出“-_-”。每组数据的结果占据一行。
示例:
输入
8 8
########
#M####.#
#..#..C#
#..#..##
#..#..##
#.##...#
#......#
########
3 5
#####
#M#C#
#####
0 0
输出
^_^
-_-
代码如下:
#include <stdio.h>
#include <stdlib.h>
int n,m,min=99999999,flag=0;
char a[21][21],book[21][21];
// 起点坐标
int startx = 1;
int starty = 1;
// 终点坐标
int finalx = 1;
int finaly = 1;
void dfs(int x,int y,int step){
// 定义一个方向数组
int next[4][2] = {
{ 0, 1}, // 向右走
{ 1,0 }, // 向下走
{ 0, -1 }, // 向左走
{ -1,0 } // 向上走
};
int tx,ty,k;
// 判断是否到达C
if ( x==finalx && y==finaly) {
if(step<min){
min = step;
flag=1;
}
return ;
}
// 枚举四种走法
for( k=0;k<=3;k++ ){
tx = x+next[k][0];
ty = y+next[k][1];
// 判断是否越界
if (tx<1 || tx > n || ty<1 || ty>m ) {
continue;
}
// 判断是否为障碍物或者已经再路径中
if ( a[tx][ty]==\'.\' && book[tx][ty]==0 ){
book[tx][ty] = 1; // 标记这个点已经走过
dfs(tx,ty,step+1); // 开始尝试下一个点
book[tx][ty] = 0; // 尝试结束,取消这个点的标记
}
}
return ;
}
int main()
{
int i,j;
// 输入n和m,n为行,m为列
scanf("%d%d",&n,&m);
getchar();
while(n!=0&&m!=0){
// 读入迷宫
for(i=1;i<=n;i++) {
for(j=1;j<=m;j++){
scanf("%c",&a[i][j]);
}
getchar();
}
// 读入起点和终点坐标
// scanf("%d %d %d %d",&startx,&starty,&p,&q);
// 找起点坐标
for(i=1;i<=n;i++){
for(j=1;j<=m;j++){
if(a[i][j]==\'M\'){
startx=i;
starty=j;
a[i][j]=\'.\';
}
}
}
// 找终点坐标
for(i=1;i<=n;i++){
for(j=1;j<=m;j++){
if(a[i][j]==\'C\'){
finalx=i;
finaly=j;
a[i][j]=\'.\';
}
}
}
// 从起点开始搜索
book[startx][starty] = 1; // 标记起点再路径中,防止后面重复走
dfs(startx,starty,0);
printf("JERRY的位置为:%d %d\\n",startx,starty);
printf("奶酪的位置为:%d %d\\n",finalx,finaly);
if(flag){
printf("^^ ^^\\n");
printf(" __\\n\\n");
printf("最少可以经过%d步找到奶酪\\n",min);
}else{
printf("不能找到奶酪!\\n");
printf("__ __\\n");
printf("\\n");
printf(" __ \\n\\n");
}
scanf("%d%d",&n,&m);
getchar();
// 起点坐标
startx = 1;
starty = 1;
// 终点坐标
finalx = 1;
finaly = 1;
flag = 0;
}
getchar();getchar();
return 0;
}
运行截图如下:
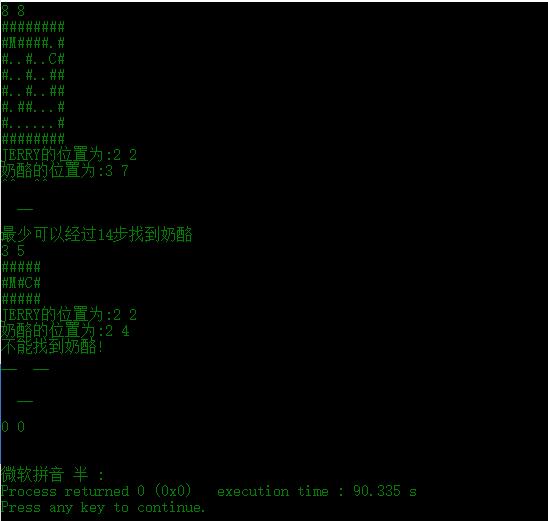
以上是关于深度优先算法--判断迷宫的一个起点能否到达一个终点的主要内容,如果未能解决你的问题,请参考以下文章