hihocoder #1467 : 2-SAT·hihoCoder音乐节 2-SAT
Posted 
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了hihocoder #1467 : 2-SAT·hihoCoder音乐节 2-SAT相关的知识,希望对你有一定的参考价值。
题目链接:
http://hihocoder.com/problemset/problem/1467
题意:
hihoCoder音乐节由hihoCoder赞助商大力主办,邀请了众多嘉宾和知名乐队参与演出。
音乐会分为上午、下午两场进行,主办方指定了n首歌让乐队进行演唱。每首歌只会被演唱一次,要么在上午要么在下午。
参加音乐会的嘉宾们对于歌曲的演唱时间有一些要求。具体来说,每位嘉宾会指定两首歌曲的演唱时间(上午或者下午)。如果最后实际的演出安排中,两首歌都没有达到嘉宾的要求,那么嘉宾就会对音乐节不滿意。如嘉宾A的要求是上午《我的滑板鞋》和下午《忐忑》,而最后的演出中上午没有《我的滑板鞋》只有《忐忑》,下午没有《忐忑》只有《我的滑板鞋》,那么嘉宾A是不满意的。
音乐节主办方自然希望使所有嘉宾满意,但主办方后来发现有可能不存在一种歌曲的安排方案满足所有嘉宾,所以他们希望你判断一下这种情况是否会发生。
输入
输入第一行包含一个数字 K,代表K组数据。(K≤50)
对于每一组数据,第一行包含两个非负整数n和m(n≤100,m≤1000),代表有n首歌和m位嘉宾。
为了方便我们给予歌编号,编号分别从1 到n。接下的m行,每行都代表对应的嘉宾的喜好由一个英文字母(m或h)跟一个数字代表,如m1 代表这个评审喜欢第1首歌上午进行,而h2代表这个评审员喜欢第2首歌下午进行。
输出
对于每一组数据,输出一行,如果能满足所有嘉宾的情况,输出GOOD;否则输出BAD。
- 样例输入
-
2 3 4 m3 h1 m1 m2 h1 h3 h3 m2 2 4 h1 m2 m2 m1 h1 h2 m1 h2
- 样例输出
-
GOOD BAD
思路:
2-SAT问题,每个嘉宾的要求就转化为一个OR,对应两条有向边,用tarjan求出强力通分量,查看每一个信息与它的反是不是在一个强联通分量里面,如果在则矛盾,否则OK,下面把提示抓过来了。
小Hi:今天是一道有关有关“推理”的题目。
小Ho:对。题目最终是要求判断会不会出现不能满足所有嘉宾的情况。我们要通过已知的信息得出矛盾。
小Hi:嗯。那我们先考虑逻辑推理的过程:如果甲喜欢上午x和另一个选项C1,乙喜欢下午x和另一个选项C2。则如果选择上午x,则不能选下午x,为了满足乙,所以不得不选C2。同理,如果做下午x,则必须选C1。
小Ho:是这样没错,那么怎么判断是否矛盾呢?
小Hi:矛盾出现的原因是一首歌不能上午和下午都唱。也就是说,对于某首歌x,如果通过逻辑推理,得出这样的结论:要x上午唱就必须选x下午唱,并且要x下午唱就必须选x上午唱。那么,这时候就矛盾了。
小Ho:说得对,那我们怎么通过编程的方式解决呢?
小Hi:这其实是一个经典的2-SAT问题,是一种特殊的逻辑判定问题。我先给你简单介绍一下,更多内容可以参考一下[wikipedia上的词条]。
小Ho:好!
小Hi:2SAT问题是这样一类问题。假设我们有N个布尔变量x1, x2, ... xN,布尔变量是指每个xi的取值是真(T)或者假(F)。然后我们还有一个表达式
f=(a1 OR b1) AND (a2 OR b2) AND ... AND (am or bm)
小Hi:其中ai, bi是xi或者?xi(非xi)。比如(x1 OR x2) AND (x1 OR ?x3) AND (?x1 OR ?x2)。直观来说就是一堆OR用AND连起来,其中每个OR都只包含两个变量。最后的问题是存不存在xi的一种取值使得f的值是真。
小Ho:2SAT和我们这道音乐节的题目又有什么关系呢?
小Hi:我们可以把n首歌曲看作n个布尔变量x1, x2, ...xn。题目中规定的"一首歌曲只演唱一次,要么要么下午"恰好对应每个xi的取值只能为真或假。假设我们认为上午演唱对应真,下午演唱对应假,那么我们就可以把嘉宾的要求转换成2SAT中的表达式。小Ho你想想"m3 h1"可以转换成哪个表达式?
小Ho:"m3 h1"代表或者上午演唱第3首,或者下午演唱第一首,也就是x3=TRUE OR x1=FALSE。
小Hi:没错。不过我们可以把表达式里的相等判断省略掉,就是(x3 OR ?x1)。
小Ho:原来如此,这样每个嘉宾的要求就转化为一个OR,m个嘉宾的要求就转化为用AND连起来的m和OR。比如样例就变成了
f = (x3 OR ?x1) AND (x1 OR x2) AND (?x1 OR ?x3) AND (?x3 OR x2)
小Ho:最后我们要求的就是这个表达式能不能成立!那么怎么f判断是能成立,还是有矛盾不能成立呢?
小Hi:我们把这个问题转化成一个图论问题来解决。首先我们对第x首歌定义两个顶点x和?x,分别代表x是真(在上午演唱)和假(在下午演唱)。另外我们根据嘉宾的要求在顶点之间连有向边。因为a OR b 等价于 ?a->b AND ?b->a,所以对于一个要求a OR b,我们连?a->b和?b->a两条边。例如"m3 h1"我们知道可以表示为(x3 OR ?x1),会添加两条边?x3->?x1和x1->x3。如果a->b有一条边,意味着如果a成立(某首歌在某个时间演唱)那么必然b成立。
小Hi:于是我们可以得到一个有向图:
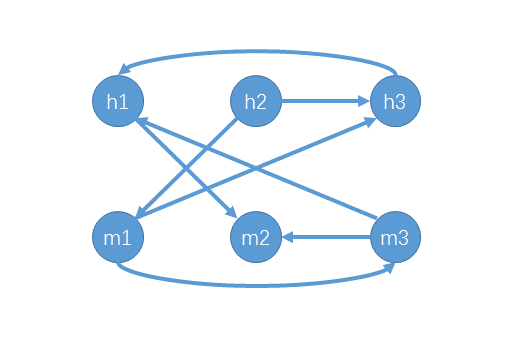
小Hi:如果该图中有同一首歌的两个点在一个环中,则无解,否则一定有解。
小Ho:我想想。因为如果a能通过边走到b,则选a就能推出选b。换到这道题目,所有如果同一首歌两个点能相互到达,而这两个点必选其一,但我们又不得不同时选,所以就矛盾了。
小Hi:没错。
小Ho:那怎么判断两个点是否在同一个环中呢?
小Hi:最暴力的方法就是直接使用广度优先搜索判断一个点是否可以到另一个点反之亦然。当然学过强连通分量的同学,求出强连通分量之后判断两个点是否在一个连通分量里即可。如何求强连通分量可以参考[这里]。
小Ho:确实是这样。那我明白了,我这就去实现一下。
代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define MS(a) memset(a,0,sizeof(a)) 5 #define MP make_pair 6 #define PB push_back 7 const int INF = 0x3f3f3f3f; 8 const ll INFLL = 0x3f3f3f3f3f3f3f3fLL; 9 inline ll read(){ 10 ll x=0,f=1;char ch=getchar(); 11 while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} 12 while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} 13 return x*f; 14 } 15 ////////////////////////////////////////////////////////////////////////// 16 const int maxn = 1e5+10; 17 18 int n,m,tot; 19 int low[maxn],dfn[maxn],vis[maxn],ins[maxn],r[maxn]; 20 stack<int> s; 21 vector<int> g[maxn]; 22 // int ne[maxn],head[maxn],to[maxn]; 23 24 void add(int a,int b){ 25 g[a].push_back(b); 26 } 27 // void addedge(int a,int b) 28 // { 29 // ne[tot]=head[a]; 30 // head[a]=tot; 31 // to[tot++]=b; 32 // } 33 34 void init(){ 35 tot = 0; 36 for(int i=0; i<=2*n; i++) 37 low[i]=dfn[i]=vis[i]=ins[i]=r[maxn] = 0, g[i].clear(); 38 while(!s.empty()) s.pop(); 39 } 40 41 void tarjan(int u){ 42 low[u] = dfn[u] = ++tot; 43 vis[u] = ins[u] = 1; 44 s.push(u); 45 for(int i=0; i<(int)g[u].size(); i++){ 46 int v = g[u][i]; 47 // for(int i=head[u];~i;i=ne[i]){ 48 // int v=to[i]; 49 if(!vis[v]){ 50 tarjan(v); 51 low[u] = min(low[u],low[v]); 52 }else if(ins[v]){ 53 low[u] = min(low[u],dfn[v]); 54 } 55 } 56 57 if(low[u] == dfn[u]){ 58 int t=0; 59 do{ 60 t = s.top(); s.pop(); 61 r[t] = u; 62 ins[t] = 0; 63 }while(t != u); 64 } 65 } 66 67 int main(){ 68 int T; 69 cin >> T; 70 while(T--){ 71 // memset(head,-1,sizeof(head)); 72 init(); 73 scanf("%d%d",&n,&m); 74 for(int i=1; i<=m; i++){ 75 char s1[5],s2[5]; 76 scanf("%s",s1); 77 int a; 78 sscanf(s1+1,"%d",&a); 79 a = a*2-1; 80 if(s1[0] == ‘h‘) a--; 81 scanf("%s",s2); 82 int b; 83 sscanf(s2+1,"%d",&b); 84 b = b*2-1; 85 if(s2[0] == ‘h‘) b--; 86 add(a^1,b); 87 add(b^1,a); 88 // addedge(a^1,b); 89 // addedge(b^1,a); 90 } 91 for(int i=0; i<2*n; i++){ 92 if(!dfn[i]) tarjan(i); 93 } 94 95 bool f = 1; 96 for(int i=0; i<2*n; i+=2){ 97 if(r[i] == r[i+1]){ 98 f = 0; 99 break; 100 } 101 } 102 if(f) puts("GOOD"); 103 else puts("BAD"); 104 } 105 106 return 0; 107 }
以上是关于hihocoder #1467 : 2-SAT·hihoCoder音乐节 2-SAT的主要内容,如果未能解决你的问题,请参考以下文章
hihocoder #1468 : 2-SAT·hihoCoder新春晚会 2-SAT
hiho一下第133周 2-SAT·hihoCoder音乐节(2-SAT)(强连通)
hiho一下第134周 1468 : 2-SAT·hihoCoder新春晚会