机器学习-广义线性模型
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习-广义线性模型相关的知识,希望对你有一定的参考价值。
广义线性模型是把自变量的线性预测函数当作因变量的估计值。在机器学习中,有很多模型都是基于广义线性模型的,比如传统的线性回归模型,最大熵模型,Logistic回归,softmax回归,等等。今天主要来学习如何来针对某类型的分布建立相应的广义线性模型。
Contents
1. 广义线性模型的认识
2. 常见概率分布的认识
1. 广义线性模型的认识
首先,广义线性模型是基于指数分布族的,而指数分布族的原型如下
为自然参数,它可能是一个向量,而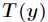 叫做充分统计量,也可能是一个向量,通常来说
叫做充分统计量,也可能是一个向量,通常来说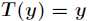 。
。
服从高斯分布,那么
是线性最小二乘回归,当随机变量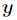 服从伯努利分布,则得到的是Logistic回归。
服从伯努利分布,则得到的是Logistic回归。
那么如何根据指数分布族来构建广义线性模型呢? 首先以如下三个假设为基础
(1)给定特征属性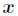 和参数
和参数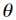 后,
后,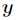 的条件概率
的条件概率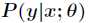 服从指数分布族,即
服从指数分布族,即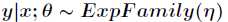 。
。
预测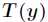 的期望,即计算
的期望,即计算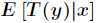 。
。
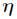 与
与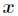 之间是线性的,即
之间是线性的,即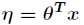 。
。
在讲解利用广义线性模型推导最小二乘和Logistic回归之前,先来认识一些常见的分布,这是后面的基础。
(1)高斯分布
关于高斯分布的内容我就不再多讲了,如果把它看成指数分布族,那么有
对比一下指数分布族,可以发现
所以高斯分布实际上也是属于指数分布族,线性最小二乘就是基于高斯分布的。
(2)伯努利分布
伯努利分布又叫做两点分布或者0-1分布,是一个离散型概率分布,若伯努利实验成功,则伯努利随机变
1,如果失败,则伯努利随机变量取值为0。并记成功的概率为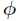 ,那么失败的概率就是
,那么失败的概率就是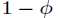 ,
,
所以得到其概率密度函数为
如果把伯努利分布写成指数分布族,形式如下
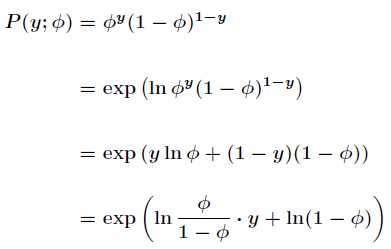
Logistic回归就是基于伯努利分布的,之前的Sigmoid函数,现在我们就可以知道它是如何来的了。如下
如果
叫做正则响应函数,而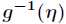 叫做正则关联函数。
叫做正则关联函数。
(3)泊松分布
只能取非负整数值0,1,2,... 且其概率密度函数为
是泊松分布的均值,也是泊松分布的方差,表示单位时间内随机事件的平均发生率。在实际
的实例中,近似服从泊松分布的事件有:某电话交换台收到的呼叫,某个网站的点击量,来到某个公共
汽车站的乘客,某放射性物质发射出的粒子,显微镜下某区域内的白血球等计数问题。
http://zh.wikipedia.org/wiki/%E6%B3%8A%E6%9D%BE%E5%88%86%E4%BD%88
关于概率论中的分布主要介绍这几个,其中还有很多分布都属于指数分布族,比如伽马分布,指数分布,多
元高斯分布,Beta分布,Dirichlet分布,Wishart分布等等。根据这些分布的概率密度函数可以建立相
应的模型,这些都是广义线性模型的一个实例。
以上是关于机器学习-广义线性模型的主要内容,如果未能解决你的问题,请参考以下文章
机器学习 —— 基础整理:线性回归;二项Logistic回归;Softmax回归;广义线性模型