机器学习 —— 基础整理：线性回归；二项Logistic回归；Softmax回归；广义线性模型

Posted 2020-09-12 Determined22

     本文简单整理了以下内容：

（一）线性回归

（二）二分类：二项Logistic回归

（三）多分类：Softmax回归

（四）广义线性模型 

      闲话：二项Logistic回归是我去年入门机器学习时学的第一个模型（忘记了为什么看完《统计学习方法》第一章之后直接就跳去了第六章，好像是对“逻辑斯蒂”这个名字很感兴趣？。。。），对照《机器学习实战》写了几行代码敲了一个toy版本，当时觉得还是挺有意思的。我觉得这个模型很适合用来入门（但是必须注意这个模型有很多很多很多很多可以展开的地方）。更有意思的是那时候还不会矩阵微积分，推导梯度时还是把矩阵全都展开求然后再归纳成矩阵形式的（牛顿法要用的二阶梯度也是）。。。

 

      下面的文字中，“Logistic回归”都表示用于二分类的二项Logistic回归。

      首先约定一下记号。

      样本的特征矩阵 $X=(\\textbf x_1,\\textbf x_2,...,\\textbf x_N)=({\\textbf x^{(1)}}^{\\top};{\\textbf x^{(2)}}^{\\top};...;{\\textbf x^{(d)}}^{\\top})\\in\\mathbb R^{d\\times N}$ ，$X_{ji}=x_i^{(j)}$；

      $N$ 是训练集的样本数，每个样本都表示成 $\\textbf x_i\\in\\mathbb R^d$ 的列向量，真实标签为 $y_i$ ；如果出现了 $\\textbf x$ 这样没有上下标的记号就泛指任一样本，相当于省略下标，真实标签为 $y$ ；特别地，对于二分类问题，$y$ 只可能取0、1两个值。

      $d$ 是特征的维数，每维特征都表示成 $\\textbf x^{(j)}\\in\\mathbb R^N$ 的列向量；如果出现了 $x^{(j)}$ 这样的记号就泛指任一样本的第 $j$ 维特征，相当于省略下标；

      权重向量 $\\textbf w=(w_1,w_2,...,w_d)^{\\top}\\in\\mathbb R^d$ ，偏置 $b\\in\\mathbb R$ 。

      $\\textbf y$ 在本文可能表达两种含义：一种是表示全部训练样本的真实标签组成的列向量 $\\textbf y=(y_1,y_2,...,y_N)^{\\top}\\in\\mathbb R^N$ ；另一种含义则是表示样本 $\\textbf x$ 的one-hot表示 $\\textbf y=(0,0,...,0,1,0,...,0)^{\\top}\\in\\mathbb R^C$（只有真实类别的那一维是1，其他维均是0），相当于 $\\textbf y_i$ 省略了下标。

      可能看起来有点别扭，因为对于样本来说，下标是序号索引、上标是特征索引；而对于权重来说，下标是特征索引。

（一）线性回归

    1. 概述

      线性回归（Linear regression）就是用一个超平面去拟合样本点的标签：

$$f(\\textbf x)=\\textbf w^{\\top}\\textbf x+b$$

      对于一维特征的情况，就是用一条直线去拟合样本点，如下图所示。为了方便起见，将偏置也记到权重向量中并保持记号不变，同时每个样本增加一维特征并保持记号不变：$\\textbf w=(1,w_1,w_3,...,w_d)^{\\top}$ ，$\\textbf x=(1,x^{(1)},x^{(2)},...,x^{(d)})^{\\top}$ ，$f(\\textbf x)=\\textbf w^{\\top}\\textbf x$ 。

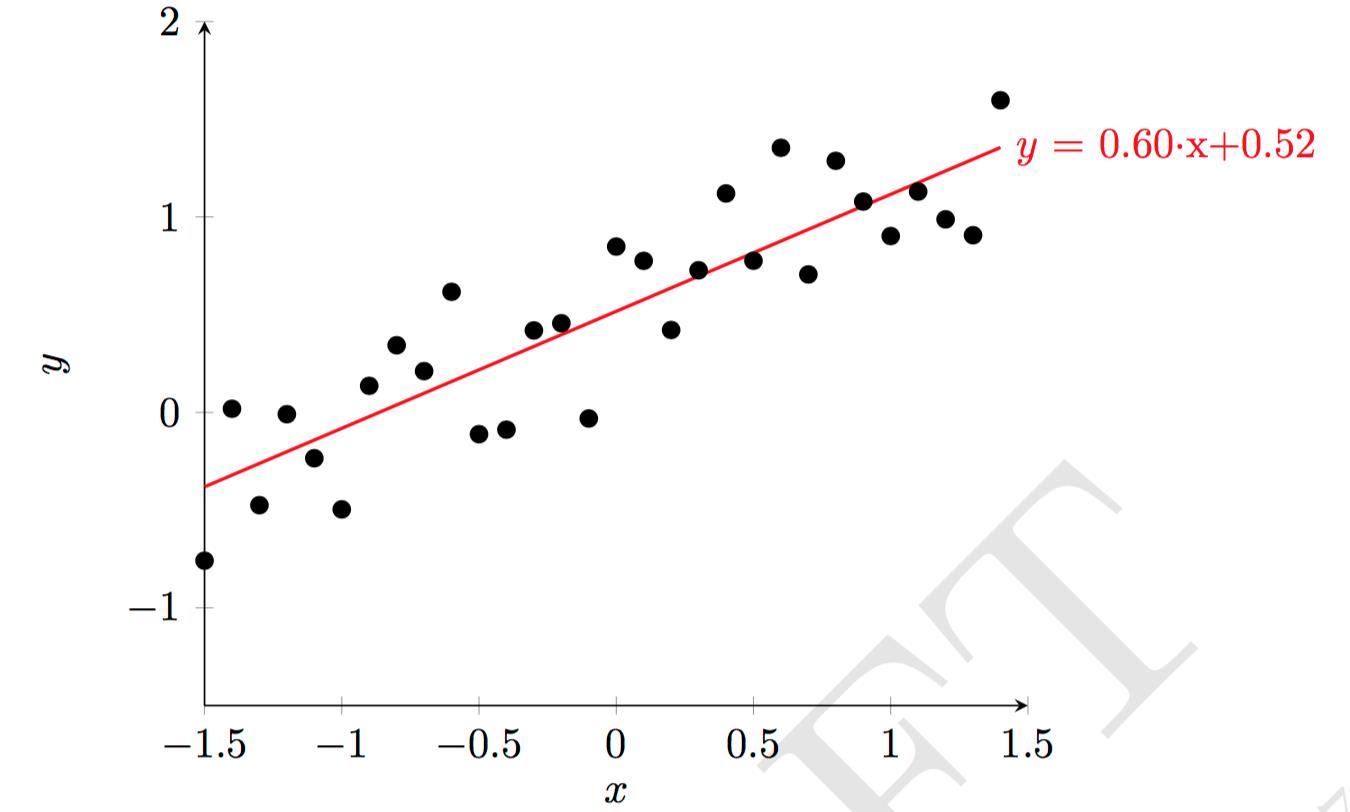
图片来源：[1]

      2. 求解

      对于回归任务，最常使用的损失函数是平方损失函数 $L(y,f(\\textbf x))=(y-f(\\textbf x))^2$ ，对应的经验风险就是均方误差（Mean square error，MSE）：

$$\\mathcal R=\\frac1N\\sum_{i=1}^N(y_i-f(\\textbf x_i))^2=\\frac1N\\|X^{\\top}\\textbf w-\\textbf y\\|^2=\\frac1N(X^{\\top}\\textbf w-\\textbf y)^{\\top}(X^{\\top}\\textbf w-\\textbf y)$$

该式的 $\\textbf y$ 表示全部训练样本的真实标签组成的列向量 $\\textbf y=(y_1,y_2,...,y_N)^{\\top}\\in\\mathbb R^N$ 。

      解一：正规方程组（Normal equations）。可以直接用 $R$ 的一阶导数等于0来求极值点（省略常系数）：

$$\\frac{\\partial \\mathcal R}{\\partial\\textbf w}=2X(X^{\\top}\\textbf w-\\textbf y)=0\\Rightarrow \\textbf w=(XX^{\\top})^{-1}X\\textbf y$$

      可以看出，这个不就是最小二乘法（Ordinary Least Squares，OLS）解方程 $X^{\\top}\\textbf w=\\textbf y$ 嘛。值得注意的是 $(XX^{\\top})^{-1}X$ 其实就是 $X^{\\top}$ 的伪逆，计算伪逆的复杂度很高。

      需要注意一个问题：$XX^{\\top}$ 需要是可逆矩阵，也就是说每维特征之间线性无关，才可以求得唯一解。当其不可逆（特征个数比样本个数还要多）时，解不唯一，需要用梯度下降（Gradient descent）来迭代求解。另外，最小二乘法的结果总是低偏差高方差的。

    （注：部分求导法则，使用分母布局，维度为 $q$ 的列向量对维度为 $p$ 的列向量求导后得到的矩阵维数为 $p\\times q$ 。关于矩阵求导，可以参考 [8] 。

图片来源：[1]

$$\\frac{\\partial A^{\\top}\\textbf x}{\\partial\\textbf x}=\\frac{\\partial \\textbf x^{\\top}A}{\\partial\\textbf x}=A$$

$$\\frac{\\partial \\textbf y^{\\top}\\textbf z}{\\partial\\textbf x}=\\frac{\\partial \\textbf y}{\\partial\\textbf x}\\textbf z+\\frac{\\partial \\textbf z}{\\partial\\textbf x}\\textbf y$$

$$\\frac{\\partial \\textbf y^{\\top}A\\textbf z}{\\partial\\textbf x}=\\frac{\\partial \\textbf y}{\\partial\\textbf x}A\\textbf z+\\frac{\\partial \\textbf z}{\\partial\\textbf x}A^{\\top}\\textbf y$$

$$\\frac{\\partial y\\textbf z}{\\partial\\textbf x}=\\frac{\\partial y}{\\partial\\textbf x}\\textbf z^{\\top}+y\\frac{\\partial \\textbf z}{\\partial\\textbf x}$$

$$\\frac{\\partial \\text{tr}AB}{\\partial A}=B^{\\top}\\quad\\quad\\frac{\\partial \\text{tr}AB}{\\partial A^{\\top}}=B$$

$$\\frac{\\partial f(A)}{\\partial A^{\\top}}=(\\frac{\\partial f(A)}{\\partial A})^{\\top}$$

）

      解二：最小均方误差（least mean squares，LMS）规则，也叫Widrow-Hoff规则，用梯度下降法求解。梯度在上面已经求出来了：

$$\\frac{\\partial \\mathcal R}{\\partial\\textbf w}=2X(X^{\\top}\\textbf w-\\textbf y)=2X(\\hat{\\textbf y}-\\textbf y)$$

该式的 $\\hat{\\textbf y}$ 表示模型对全部训练样本的输出标签组成的列向量 $\\hat{\\textbf y}=(\\hat y_1,\\hat y_2,...,\\hat y_N)^{\\top}\\in\\mathbb R^N$ 。

这样的方式是每更新一次参数就要计算整个训练集上的梯度，是批梯度下降（batch GD）；如果把这个过程拆成 $N$ 次，也就是每次只随机挑选一个样本计算梯度，就是随机梯度下降（Stochastic GD，SGD）。还有一种是mini-batch梯度下降，每次挑选一个小批量样本计算梯度。整个训练集计算完一次梯度称为“一轮”。

      3. 均方误差优化目标的概率解释

      重新考虑以下问题：设样本的特征和标签存在关系 $y_i=\\textbf w^{\\top}\\textbf x_i+\\epsilon_i$ ，并假设每个 $\\epsilon_i$ 都是服从高斯分布的随机变量 $\\epsilon\\sim N(0,\\sigma^2)$ 的iid样本（之所以假设为高斯分布，是认为误差由多个独立的随机因素构成，根据多个独立随机变量之和趋于高斯分布，所以假设 $\\epsilon$ 服从高斯分布）。从而有

$$p(\\epsilon_i)=\\frac1{\\sqrt{2\\pi}\\sigma}\\exp(-\\frac{\\epsilon_i^2}{2\\sigma^2})$$

也就是说

$$p(y_i|\\textbf x_i;\\textbf w)=\\frac1{\\sqrt{2\\pi}\\sigma}\\exp(-\\frac{(y_i-\\textbf w^{\\top}\\textbf x_i)^2}{2\\sigma^2})$$

用分号隔开是因为在频率学派的观点下 $\\textbf w$ 不是随机变量。

      进一步用极大似然估计来求取参数 $\\textbf w$ ：对数似然函数为

$$l(\\textbf w)=\\log\\prod_{i=1}^Np(y_i|\\textbf x_i;\\textbf w)=\\log\\prod_{i=1}^N\\frac1{\\sqrt{2\\pi}\\sigma}\\exp(-\\frac{(y_i-\\textbf w^{\\top}\\textbf x_i)^2}{2\\sigma^2})$$

再往后写一步就可以知道，极大似然估计和最小化均方误差是一致的。

      4. 局部加权回归（Locally weighted regression，LWR）

      相比于普通的线性回归，LWR对于一个点来说使用其附近的点来做回归（而不是全部点）。

      相比于线性回归的优化目标 $\\sum_{i=1}^N(y_i-\\textbf w^{\\top}\\textbf x_i)^2$ ，局部加权线性回归的优化目标为

$$\\sum_{i=1}^N\\omega_i(y_i-\\textbf w^{\\top}\\textbf x_i)^2$$

式中 $\\omega_i$ 就是非负值的权重，一个常用的选择为 $\\omega_i=\\exp(-\\frac{(\\textbf x_i-\\textbf x)^{\\top}(\\textbf x_i-\\textbf x)}{2\\tau^2})$ ，$\\tau$ 是指定的带宽参数（bandwidth）。不难看出，LWR每预测一个点的值都要重新得到一个新的模型。

 

（二）二项Logistic回归

    1. 概述

      对于分类任务，一个可行的思路是把基于样本 $\\textbf x$ 计算出的连续值 $z$（比如，线性加权值 $z=\\textbf w^{\\top}\\textbf x$ ）和离散的类别标签值联系起来。

      二项Logistic回归（Binomial logistic regression）是工业界应用非常广泛的一个经典的二分类模型。一般就叫逻辑回归，这里无意争论到底应该怎么翻译，虽然古人云“名不正则言不顺”，但提起“逻辑回归”大家都知道这是哪个东西，我觉得这就够了。对Logistic回归的历史感兴趣的朋友们可以看一下 [7] 的介绍。首先使用logistic函数 $\\sigma(\\cdot)$ 将 $ z$ 从实数空间 $(-\\infty,+\\infty)$ 映射到概率空间 $(0,1)$ 上，可以将映射之后的值 $\\sigma(z)$ 解释为样本 $\\textbf x$ 属于正类（记类别标记为1）的可能性，也就是后验概率的估计值：

$$\\hat y=P(y=1|\\textbf x)=\\sigma(z)=\\frac{1}{1+\\exp(-z)}$$

      既然解释成后验概率，然后就可以给出分类规则（最大后验概率决策）：当 $P(y=1|\\textbf x)>0.5$ ，认为样本 $\\textbf x$ 属于正类；否则样本 $\\textbf x$ 属于正类属于负类。

      下面两个图是一维特征、二分类的情况。大致说了线性回归为什么不可以用来分类。因为线性回归输出连续值，而类别标签只有0、1两个，所以需要人为设定一个阈值，将输出值与该值比较大小，从而来判断模型将样本分到哪一类，而这个阈值会受到离群点（outlier）的牵制，因为线性回归的拟合曲线会因为离群点而受到较大影响，所以不好确定；相比之下，logistic回归不会受到图示离群点的牵制。

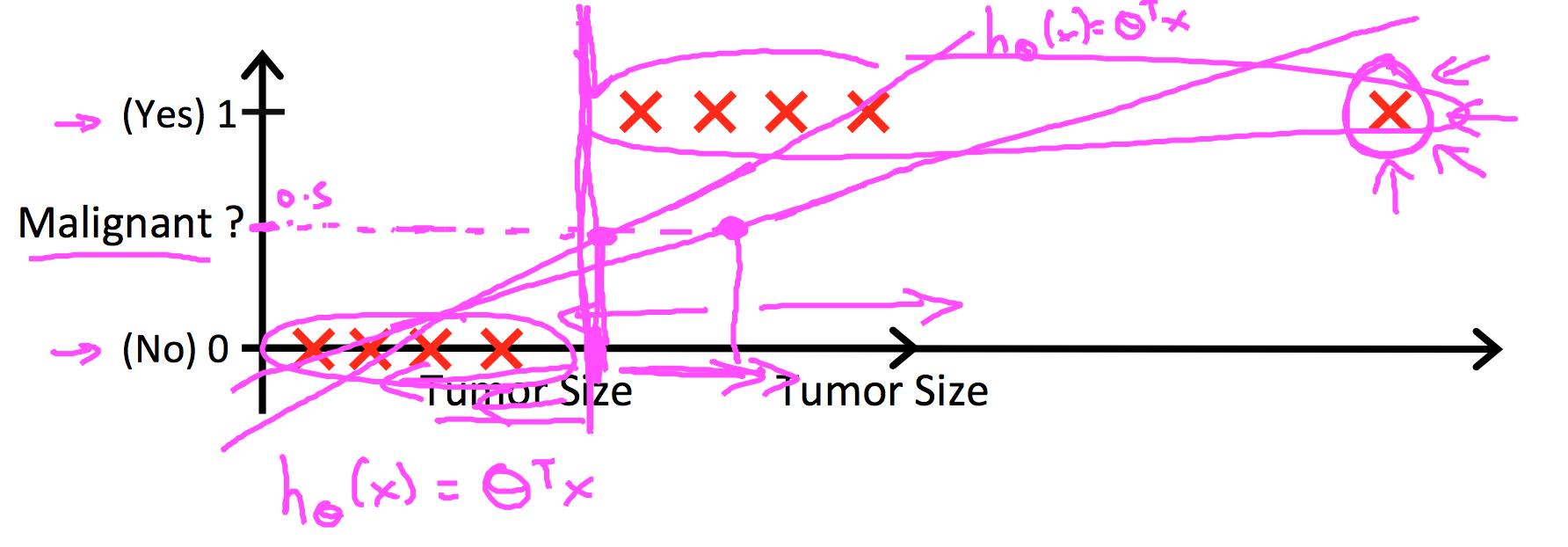
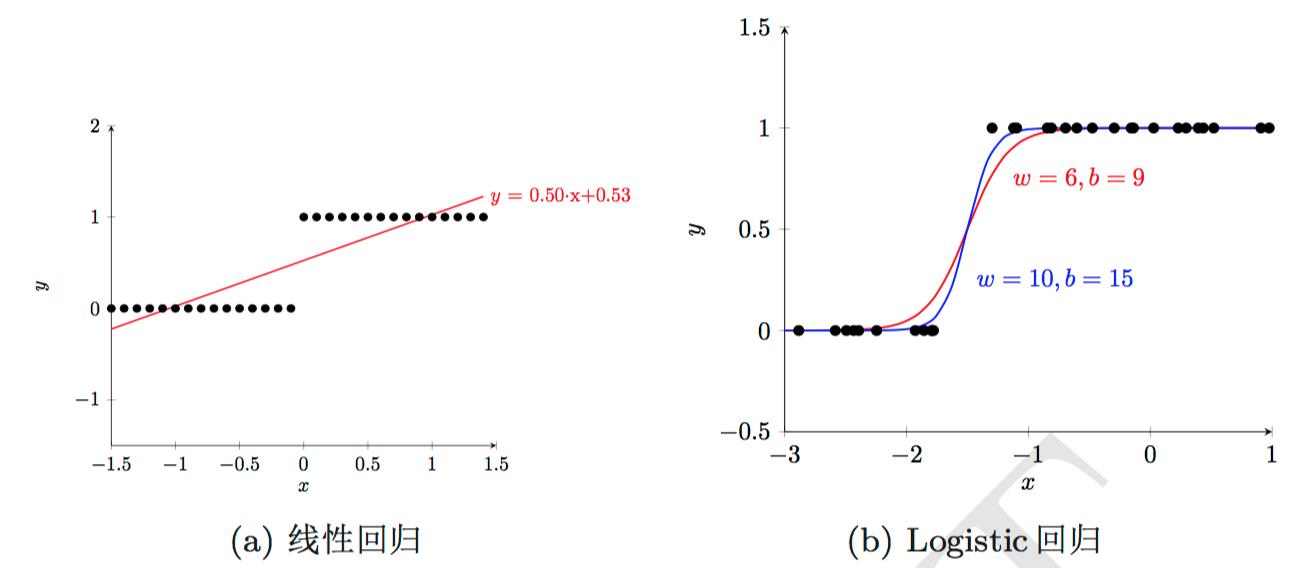
图片来源：[5]、[1]

      待补充：为什么使用logistic函数归到区间 $(0,1)$ 之后就可以解释成概率了。

      2. 决策边界

      下面说一下决策边界。当 $P(y=1|\\textbf x)=0.5$ 时，意味着 $z=0$ ，这就是决策边界的方程。换句话说，$z$ 的形式决定了逻辑回归的决策面是线性的还是非线性的。如果 $z=\\textbf w^{\\top}\\textbf x$ ，那决策面当然是线性的；但是如果 $z$ 的形式并不是特征的线性组合，而是非线性的形式，当然也可以是非常复杂的决策面。

图片来源：[1]

      下面我们只讨论线性决策面的情况。Logistic回归模型为：

$$\\hat y=P(y=1|\\textbf x)=\\sigma(\\textbf w^{\\top}\\textbf x)=\\frac{\\exp(\\textbf w^{\\top}\\textbf x)}{1+\\exp(\\textbf w^{\\top}\\textbf x)}$$

$$P(y=0|\\textbf x)=1-\\sigma(\\textbf w^{\\top}\\textbf x)=\\frac{1}{1+\\exp(\\textbf w^{\\top}\\textbf x)}$$

      稍加变换就可以看出Logistic回归和线性回归的区别：

      线性回归是用 $\\textbf w^{\\top}\\textbf x$ 去拟合 $y$ ；二项Logistic回归则是去拟合 $\\ln \\dfrac{\\hat y}{1-\\hat y}$ ，换句话说就是在拟合对数几率（log-odds，几率是样本属于正类的可能性与属于负类的可能性的比值）。也就是说，二项Logistic回归在对对数几率做回归，进而转化为解决分类问题。

      3. 求解

      （1）经验风险最小化：极大似然估计

      logistic函数 $\\sigma(\\cdot)$ 的导函数为 $\\sigma\'(\\cdot)=\\sigma(\\cdot)\\odot (\\textbf 1-\\sigma(\\cdot))$ 。也就是说当自变量为向量时，函数对逐元素进行计算，输出同维度的向量。

      首先从经验风险最小化的角度推导参数的求解过程。使用交叉熵损失函数（单标签情况下就是对数损失函数），模型对一个样本 $(\\textbf x,y)$ 的对数损失为：

$$\\begin{aligned}\\mathcal L&=-\\biggl(y\\ln P(y=1|\\textbf x)+(1-y)\\ln P(y=0|\\textbf x)\\biggr)\\\\&=-\\biggl(y\\ln\\frac{\\exp(\\textbf w^{\\top}\\textbf x)}{1+\\exp(\\textbf w^{\\top}\\textbf x)}+(1-y)\\ln\\frac{1}{1+\\exp(\\textbf w^{\\top}\\textbf x)}\\biggr)\\\\&=-\\biggl(y\\textbf w^{\\top}\\textbf x-\\ln(1+\\exp(\\textbf w^{\\top}\\textbf x))\\biggr)\\end{aligned}$$

      所以经验风险为：

$$\\mathcal R=\\frac1N\\sum_{i=1}^N\\mathcal L_i=-\\frac1N\\sum_{i=1}^N\\biggl(y_i\\textbf w^{\\top}\\textbf x_i-\\ln(1+\\exp(\\textbf w^{\\top}\\textbf x_i))\\biggr)$$

      如果不加正则的话，优化目标为上式最小化。前面的系数 $\\dfrac1N$ 也就是训练样本数的倒数，是定值，去掉后不影响优化目标。 

      从极大似然估计的角度也可以推出等价的优化目标：对数似然函数为

$$\\begin{aligned}l(\\textbf w)&=\\ln[\\prod_{i=1}^NP(y_i|\\textbf x_i;\\textbf w)]\\\\&=\\ln[\\prod_{i=1}^NP(y_i=1|\\textbf x_i)^{y_i}P(y_i=0|\\textbf x_i)^{1-y_i}]\\\\&=\\sum_{i=1}^N\\biggl(y_i\\ln P(y_i=1|\\textbf x_i)+(1-y_i)\\ln P(y_i=0|\\textbf x_i)\\biggr)\\end{aligned}$$

该式最大化就等价于经验风险最小化。

      由于优化目标求不出解析解，但它是高阶连续可微的凸函数，所以可以用迭代的方法，如梯度下降法（GD）。

      因为SGD每次迭代是随机选择一个样本，所以这里先求取模型对一个样本的损失的梯度（经验风险的梯度无非就是加个求和号再除以训练样本数而已）：

$$\\frac{\\partial \\mathcal L}{\\partial\\textbf w}=-\\biggl(y\\textbf x-\\textbf x\\frac{\\exp(\\textbf w^{\\top}\\textbf x)}{1+\\exp(\\textbf w^{\\top}\\textbf x)}\\biggr)$$

可以发现其实它就是个特别简单的形式：

$$\\frac{\\partial \\mathcal L}{\\partial\\textbf w}=-(y-\\hat y)\\textbf x$$

      经验风险的梯度可以写成矩阵的形式（ $\\textbf y$ 表示训练集样本的真实标签组成的列向量），省略系数 $\\dfrac1N$ ：

$$\\begin{aligned}\\frac{\\partial \\mathcal R}{\\partial\\textbf w}&=-\\sum_{i=1}^N (y_i-\\sigma(\\textbf w^{\\top}\\textbf x_i))\\textbf x_i\\\\&= -X(\\textbf y-\\sigma(X^{\\top}\\textbf w))\\\\&= -X(\\textbf y-\\hat{\\textbf y})\\end{aligned}$$

可以很容易把这种批处理GD的形式改写成mini-batch SGD的形式。

      不难看出，这个梯度形式和线性回归是一样的。（后面会知道，Softmax回归的梯度形式和它们也是一样的。）

      这里顺便把二阶梯度也求一下，可以使用牛顿法或拟牛顿法来迭代求取参数：

$$\\frac{\\partial \\mathcal L}{\\partial\\textbf w}=-(y-\\sigma(\\textbf w^{\\top}\\textbf x))\\textbf x=\\sigma(\\textbf w^{\\top}\\textbf x)\\textbf x -y\\textbf x$$

$$\\begin{aligned}\\frac{\\partial^2\\mathcal L}{\\partial\\textbf w^2}&=\\frac{\\partial(\\sigma(\\textbf w^{\\top}\\textbf x)\\textbf x -y\\textbf x)}{\\partial\\textbf w}\\\\&=\\frac{\\sigma(\\textbf w^{\\top}\\textbf x)}{\\partial\\textbf w}\\textbf x^{\\top}\\\\&=\\sigma(\\textbf w^{\\top}\\textbf x)(1-\\sigma(\\textbf w^{\\top}\\textbf x))\\textbf x\\textbf x^{\\top}\\\\&=\\hat y(1-\\hat y)\\textbf x\\textbf x^{\\top}\\end{aligned}$$

$$\\frac{\\partial^2\\mathcal R}{\\partial\\textbf w^2}=\\sum_{i=1}^N\\hat y_i(1-\\hat y_i)\\textbf x_i\\textbf x_i^{\\top}$$

      （2）结构风险最小化：最大后验概率估计

      如果将正则项加上，那就是用结构风险最小化的准则来学习参数，常用的有参数的 $L_1$ 范数（LASSO）和 $L_2$ 范数（Ridge）：

$$R_{\\text{srm}}=R+\\lambda\\|\\textbf w\\|_1$$

$$R_{\\text{srm}}=R+\\lambda\\|\\textbf w\\|_2^2$$

从梯度的形式来看，相比于不加正则的时候，变化量为

$$\\frac{\\partial \\|\\textbf w\\|_1}{\\partial w_j}=\\frac{\\partial \\sum_{j=1}^d|w_j|}{\\partial w_j}=1\\text{ if }w_j>0\\text{ else if }w_j<0\\,-1$$

$$\\frac{\\partial \\|\\textbf w\\|_2^2}{\\partial w_j}=\\frac{\\partial \\sum_{j=1}^d|w_j|^2}{\\partial w_j}=2w_j$$

如果 $w_j$ 为正，那么新迭代点相比之前会减去一个正数而变小；如果 $w_j$ 为负，那么新迭代点相比之前会减去一个负数而变大。也就是说避免了特别大或者特别小的权重值出现，可以使权重的绝对值变小，从而避免过于依赖某些特征的情况，减轻过拟合。

      加 $L_1$ 正则时会使某些维的参数变成0，这就是所谓的稀疏解，相当于进行了一个特征选择的过程；加 $L_2$ 正则时权重的绝对值会变小，起到平滑化的作用。更详细地可以参考[4]。

      4. 贝叶斯角度

      如果从贝叶斯估计的角度来说，正则项相当于加上了先验知识：加 $L_1$ 正则相当于是认为参数服从Laplace分布，加 $L_2$ 正则相当于是认为参数服从均值为0、协方差为 $\\frac{1}{\\lambda}$ 的高斯分布。此时，结构风险最小化等价于最大后验概率估计。具体可以参考[6][9]。

      5. 与其他模型的关系

      最显然的一个就是全连接的前馈神经网络就是多层Logistic回归模型（不知道为什么被叫成MLP，多层感知机）。其与朴素贝叶斯的联系可以看本系列博客第二篇。更详细地请参考 [7] ，后面有空的话会简单谈一点。

      6. 并行

      这里参考[7]。

      

（三）Softmax回归

      Softmax回归可以用于多类分类问题，而不像Logistic回归等二分类模型那样需要借助One-vs-rest。设样本 $\\textbf x_i$ 的真实类别标签 $y_i\\in\\{1,2,...,C\\}$ ，one-hot向量为 $\\textbf y_i=(0,0,...,0,1,0,...,0)^{\\top}\\in\\mathbb R^C$ （只有真实类别的那一维是1）。

      与Logistic回归类似，Softmax回归输出的是样本 $\\textbf x_i$ 属于各个类别的后验概率的估计值 $P(y_i=c|\\textbf x_i),c\\in\\{1,2,...,C\\}$ ：

$$z_c=\\textbf w_c^{\\top}\\textbf x_i$$

$$\\begin{aligned}P(y_i=c|\\textbf x_i)&=\\text{softmax}(z_c)\\\\&=\\frac{\\exp(z_c)}{\\sum_{j=1}^C\\exp(z_j)}\\\\&=\\frac{\\exp(\\textbf w_c^{\\top}\\textbf x_i)}{\\sum_{j=1}^C\\exp(\\textbf w_j^{\\top}\\textbf x_i)},\\quad c\\in\\{1,2,...,C\\}\\end{aligned}$$

      将模型对一个样本 $(\\textbf x_i,\\textbf y_i)$ 的后验概率估计组成列向量

$$\\hat{\\textbf y}_i=(P(y_i=1|\\textbf x),P(y_i=2|\\textbf x),...,P(y_i=C|\\textbf x))^{\\top}\\in\\mathbb R^C$$

并将各个类别的权重向量 $\\textbf w_c\\in\\mathbb R^d$ 组成权重矩阵 $W=(\\textbf w_1,\\textbf w_2,...,\\textbf w_C)\\in\\mathbb R^{d\\times C}$ ，可以写成如下形式：

$$\\textbf z_i=(z_1,z_2,...,z_C)^{\\top}=W^{\\top}\\textbf x_i$$

$$\\begin{aligned}\\hat{\\textbf y}_i&=\\text{softmax}(\\textbf z_i)=\\frac{\\exp(\\textbf z_i)}{\\sum_{j=1}^C\\exp(z_j)}\\\\&=\\frac{\\exp(W^{\\top}\\textbf x_i)}{\\sum_{j=1}^C\\exp(\\textbf w_j^{\\top}\\textbf x)}=\\frac{\\exp(W^{\\top}\\textbf x_i)}{\\textbf 1^{\\top}\\exp(W^{\\top}\\textbf x_i)}\\\\&=\\frac{\\exp(\\textbf z_i)}{\\textbf 1^{\\top}\\exp(\\textbf z_i)}\\end{aligned}$$

      使用交叉熵损失函数，模型对一个样本 $(\\textbf x_i,\\textbf y_i)$ 的损失为：

$$\\mathcal L_i=-\\textbf y_i^{\\top}\\ln\\hat{\\textbf y}_i=-\\textbf y_i^{\\top}\\ln\\text{softmax}(\\textbf z_i)=-\\textbf y_i^{\\top}\\ln\\frac{\\exp(\\textbf z_i)}{\\textbf 1^{\\top}\\exp(\\textbf z_i)}$$

所以经验风险（省略系数 $\\dfrac1N$ ）为

$$\\mathcal R=\\sum_{i=1}^N\\mathcal L_i=-\\sum_{i=1}^N\\biggl(\\textbf y_i^{\\top}\\ln\\text{softmax}(W^{\\top}\\textbf x_i)\\biggr)$$

      下面求取对一个样本 $(\\textbf x_i,\\textbf y_i)$ 的损失的梯度。先上结论：

$$\\frac{\\partial \\mathcal L_i}{\\partial\\textbf w_c}=-[\\textbf y_i-\\hat{\\textbf y}_i]_c\\textbf x_i,\\quad c\\in\\{1,2,...,C\\}$$

$$\\frac{\\partial \\mathcal L_i}{\\partial W}=-\\textbf x_i(\\textbf y_i-\\hat{\\textbf y}_i)^{\\top}$$

式中 $[\\textbf y_i]_c$ 表示的是向量 $\\textbf y_i$ 的第 $c$ 维元素的值。

      经验风险的梯度依旧可以写成矩阵的形式：

$$\\frac{\\partial \\mathcal R}{\\partial W}=\\sum_{i=1}^N\\frac{\\partial \\mathcal L_i}{\\partial W}=-X(Y-\\hat Y)$$

其中 $Y\\in\\mathbb R^{N\\times C}$ 是one-hot标签构成的矩阵，每一行都是一个样本的one-hot标签；$\\hat Y$ 含义类似。

      Softmax回归的 $\\dfrac{\\partial \\mathcal L_i}{\\partial\\textbf w_c}$ 的形式和Logistic回归的 $\\dfrac{\\partial \\mathcal L_i}{\\partial\\textbf w}$ 是一样的。

      下面给出推导过程。

      $\\dfrac{\\partial \\mathcal L_i}{\\partial\\textbf w_c}$ 的求法有三种：

      （1）普通方法，一步步推，可以参考我很早之前写的一篇讲word2vec的博客，我觉得写的还挺清楚的；

      （2）[1] 中的方法，在第三章；

      （3）[3] 中的方法，而且用这个方法可以直接把 $\\dfrac{\\partial \\mathcal L_i}{\\partial W}$ 求出来。

      $\\dfrac{\\partial \\mathcal L_i}{\\partial W}$ 推导方式可以是用 $\\dfrac{\\partial \\mathcal L_i}{\\partial\\textbf w_c}$ “拼”成对矩阵 $W$ 的梯度。下面使用 [3] 里面介绍的技巧，直接求对矩阵 $W$ 的梯度。

      [3] 介绍的是这样形式的求导：已知矩阵 $X$ ，函数 $f(X)$ 的函数值为标量，求 $\\dfrac{\\partial f}{\\partial X}$ 。一种典型的例子就是求取损失对权重矩阵的导数。

      对于一元微积分，$\\text{d}f=f\'(x)\\text{d}x$ ；多元微积分，$\\text{d}f=\\sum_i\\dfrac{\\partial f}{\\partial x_i}\\text{d}x_i=(\\dfrac{\\partial f}{\\partial \\textbf x})^{\\top}\\text{d}\\textbf x$；由此建立矩阵导数和微分的联系：

$$\\text{d}f=\\sum_{i,j}\\frac{\\partial f}{\\partial X_{ij}}\\text{d}X_{ij}=\\text{tr}((\\frac{\\partial f}{\\partial X})^{\\top}\\text{d}X)$$

      上式第二个等号成立是因为对于两个同阶方阵有 $\\text{tr}(A^{\\top}B)=\\sum_{i,j}A_{ij}B_{ij}$ 。求解的流程就是，先求微分 $\\text{d}f$ 表达式，然后再套上迹（因为标量的迹等于标量本身），然后再把表达式 $\\text{tr}(\\text{d}f)$ 和 $\\text{tr}((\\dfrac{\\partial f}{\\partial X})^{\\top}\\text{d}X)$ 进行比对，进而把 $\\dfrac{\\partial f}{\\partial X}$ 给“挖”出来。

      所以，问题就从求梯度转化成了求微分。求微分当然少不了很多法则和技巧，下面随着讲随着介绍。接下来就来求取Softmax回归中的 $\\dfrac{\\partial \\mathcal L}{\\partial W}$ （样本序号 $i$ 被省略）。

      首先求取 $\\text{d}\\mathcal L$ 。

$$\\begin{aligned}\\mathcal L&=-\\textbf y^{\\top}\\ln\\frac{\\exp(\\textbf z)}{\\textbf 1^{\\top}\\exp(\\textbf z)}\\\\&=-\\textbf y^{\\top}(\\textbf z-\\ln\\begin{pmatrix}\\textbf 1^{\\top}\\exp(\\textbf z) \\\\ \\textbf 1^{\\top}\\exp(\\textbf z) \\\\ \\vdots \\\\ \\textbf 1^{\\top}\\exp(\\textbf z)\\end{pmatrix})\\quad \\textbf 1^{\\top}\\exp(\\textbf z)\\text{是标量}\\\\&=\\ln(\\textbf 1^{\\top}\\exp(\\textbf z))-\\textbf y^{\\top}\\textbf z\\end{aligned}$$

      根据法则 $\\text{d}(g(X))=g\'(X)\\odot\\text{d}X$ 、$\\text{d}(XY)=(\\text{d}X)Y+X(\\text{d}Y)$，可得

$$\\text{d}(\\ln(\\textbf 1^{\\top}\\exp(\\textbf z)))=\\frac{1}{\\textbf 1^{\\top}\\exp(\\textbf z)}\\odot\\text{d}(\\textbf 1^{\\top}\\exp(\\textbf z))$$

$$\\text{d}(\\textbf 1^{\\top}\\exp(\\textbf z))=\\textbf 1^{\\top}\\text{d}(\\exp(\\textbf z))=\\textbf 1^{\\top}(\\exp(\\textbf z)\\odot\\text{d}\\textbf z)$$

      所以

$$\\text{d}\\mathcal L=\\frac{\\textbf 1^{\\top}(\\exp(\\textbf z)\\odot\\text{d}\\textbf z)}{\\textbf 1^{\\top}\\exp(\\textbf z)}-\\textbf y^{\\top}\\text{d}\\textbf z$$

      现在可以套上迹，根据恒等式 $\\text{tr}(A^{\\top}(B\\odot C))=\\text{tr}((A\\odot B)^{\\top}C)=\\sum_{i,j}A_{ij}B_{ij}C_{ij}$ ，可得

$$\\begin{aligned}\\text{d}\\mathcal L&=\\text{tr}(\\frac{(\\textbf 1\\odot \\exp(\\textbf z))^{\\top}\\text{d}\\textbf z}{\\textbf 1^{\\top}\\exp(\\textbf z)})-\\text{tr}(\\textbf y^{\\top}\\text{d}\\textbf z)\\\\&=\\text{tr}(\\biggl(\\frac{(\\exp(\\textbf z))^{\\top}}{\\textbf 1^{\\top}\\exp(\\textbf z)}-\\textbf y^{\\top}\\biggr)\\text{d}\\textbf z)\\\\&=\\text{tr}((\\hat{\\textbf y}-\\textbf y)^{\\top}\\text{d}\\textbf z)\\\\&=\\text{tr}((\\frac{\\partial L}{\\partial\\textbf z})^{\\top}\\text{d}\\textbf z)\\end{aligned}$$

      现在已经成功了一半，因为已经有了 $\\dfrac{\\partial \\mathcal L}{\\partial\\textbf z}$ 。因为

$$\\text{d}\\textbf z=\\text{d}(W^{\\top}\\textbf x)=(\\text{d}W^{\\top})\\textbf x+W^{\\top}\\text{d}\\textbf x=(\\text{d}W^{\\top})\\textbf x$$

并且 $\\text{tr}(ABC)=\\text{tr}(BCA)=\\text{tr}(CAB)$ ，所以有

$$\\begin{aligned}\\text{d}\\mathcal L&=\\text{tr}((\\frac{\\partial L}{\\partial\\textbf z})^{\\top}(\\text{d}W^{\\top})\\textbf x)\\\\&=\\text{tr}(\\textbf x(\\frac{\\partial L}{\\partial\\textbf z})^{\\top}\\text{d}W^{\\top})\\\\&=\\text{tr}((\\frac{\\partial L}{\\partial W^{\\top}})^{\\top}\\text{d}W^{\\top})\\end{aligned}$$

也就是说，$\\dfrac{\\partial \\mathcal L}{\\partial W^{\\top}}=\\dfrac{\\partial \\mathcal L}{\\partial\\textbf z}\\textbf x^{\\top}=(\\hat{\\textbf y}-\\textbf y)\\textbf x^{\\top}$，所以

$$\\frac{\\partial \\mathcal L}{\\partial W}=-\\textbf x(\\textbf y-\\hat{\\textbf y})^{\\top}$$

（四）广义线性模型

      其实上面介绍的三种模型，都属于广义线性模型（Generalized linear model，GLM）。

      1. 指数族分布

      说到GLM，就不得不说指数族分布。设有一随机变量 $Y$ ，观测值为 $y$ ，那么指数族分布（Exponential family distributions）的 PDF／PMF 为如下函数：

$$p(y;\\boldsymbol\\eta)=b(y)\\exp(\\boldsymbol\\eta^{\\top}T(y)-a(\\boldsymbol\\eta))$$

      式中，$\\boldsymbol\\eta$ 被称为nature parameter或canonical parameter，$T(y)$ 是充分统计量（通常设 $T(y)=y$ ），$a(\\boldsymbol\\eta)$ 是log partition function，$\\exp(-a(\\boldsymbol\\eta))$ 用来保证PDF的积分为1（或PMF的加和为1）。把随机变量服从指数族分布记为 $ Y\\sim ExponentialFamily(\\boldsymbol\\eta)$ 。伯努利分布（两点分布）、高斯分布、多项式分布、泊松分布、指数分布、伽马分布、贝塔分布、狄利克雷分布、维希特分布……等等都属于指数族分布。

      通过选取不同的 $\\boldsymbol\\eta$ ，可以得到不同的分布：

      例如，对于参数为 $\\phi$ 两点分布，其PMF为

$$P(y;\\phi)=\\phi^y(1-\\phi)^{1-y}=\\exp(y\\ln(\\frac{\\phi}{1-\\phi})+\\ln(1-\\phi))$$

所以

$$\\phi=\\frac{1}{1+\\exp(-\\eta)}$$

这正是logistic函数。

      再比如参数为均值 $\\mu$ 、方差1的高斯分布，其PDF为

$$p(y;\\mu)=\\frac{1}{\\sqrt{2\\pi}}\\exp(-\\frac12(y-\\mu)^2)=\\frac{1}{\\sqrt{2\\pi}}\\exp(-\\frac12y^2)\\exp(\\mu y-\\frac12\\mu^2)$$

所以

$$\\mu=\\eta$$

      2. 广义线性模型

      通过指数族分布，可以构建广义线性模型。设模型的参数为 $\\boldsymbol\\theta$ ，对于记 $X$ 、$Y$ 分别是代表特征和标签的随机变量，观测值为 $\\textbf x$ 、$y$ 。首先假定如下三点：

      1. 条件分布服从指数族分布，即 $Y|X;\\boldsymbol\\theta\\sim ExponentialFamily(\\boldsymbol\\eta)$ 。例如，

      2. 给定特征 $\\textbf x$ ，目标是预测 $E[T(y)|\\textbf x]$ 。因为通常设  $T(y)=y$ ，所以目标就是预测 $E[y|\\textbf x]$ 。

         实际上，就相当于对模型输出值进行预测。用Logistic回归举例：模型输出值为 $P(y=1|\\textbf x)$ ，随机变量 $Y$ 服从两点分布（只可能取0、1两个值），所以 $E[y|\\textbf x;\\boldsymbol\\theta]=0\\times P(y=0|\\textbf x)+1\\times P(y=1|\\textbf x)=P(y=1|\\textbf x)$

      3. 指数族分布的参数 $\\boldsymbol\\eta$ 和给定特征 $\\textbf x$ 的关系为线性：$\\boldsymbol\\eta=\\boldsymbol\\theta^{\\top}\\textbf x$

      下面可以开始利用不同的 $\\boldsymbol\\eta$ 来构建GLM。

      （1）线性回归

      对于第一个假设，设指数族分布是参数为 $\\mu$ 的高斯分布，即 $\\mu=\\eta$ ；那么对于第二个假设，可知模型输出值为 $\\mu$ ，结合第一个假设可知模型输出值为 $\\eta$ ；根据第三个假设 $\\boldsymbol\\eta=\\boldsymbol\\theta^{\\top}\\textbf x$ ，可知模型输出值为 $\\boldsymbol\\theta^{\\top}\\textbf x$ 。这就推导出了线性回归模型。

      （2）Logistic回归

      对于第一个假设，设指数族分布是参数为 $\\phi$ 的伯努利分布，即 $\\phi=\\frac{1}{1+\\exp(-\\eta)}$ ；那么对于第二个假设，因为伯努利分布的期望为 $\\phi$ ，可知模型输出值为 $\\phi$ ；根据第三个假设 $\\boldsymbol\\eta=\\boldsymbol\\theta^{\\top}\\textbf x$ ，可知模型输出值为 $\\phi=\\frac{1}{1+\\exp(-\\boldsymbol\\theta^{\\top}\\textbf x)}$ 。这就推导出了Logistic回归模型。

      （3）Softmax回归

      相应的指数族分布是多项式分布，代表标签的是一个随机向量 $\\boldsymbol Y$ 。详细的推导这里就不赘述了，可以参考 [5] 的最后一部分。

 

参考资料：

[1] 《神经网络与深度学习讲义》

[2] 《统计学习方法》

[3] 《矩阵求导术（上）》

[4] 机器学习中的范数规则化之（一）L0、L1与L2范数

[5] CS229 Lecture Notes1、Lecture6 slides

[6] Regularized Regression: A Bayesian point of view

[7] 浅析Logistic Regression   （写的比我这篇真的好太多了。。。）   

[8] Matrix_calculus

[9] https://www.evernote.com/shard/s146/sh/bf0d0a08-d5c5-4dc9-b70f-fa6374b9ceae/14e34bc9e8e518b1a5cc17fc585d75fc