线段树区间更新
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线段树区间更新相关的知识,希望对你有一定的参考价值。
区间更新也可以分割成若干个子区间,
每层的结点至多选取 2 个,时间复杂度 O(logn)。
懒惰(Lazy)标记
懒惰标记,也可称为延迟标记。一个区间可以转化为若干个结点,每个结点设一个标记,记录这个结点被进行了某种修改操作(这种修改操作会影响其子结点)。
也就是说,仅修改到这些结点,暂不修改其子结点;而后决定访问其子节点时,再下传懒惰 (Lazy) 标记,并消除原来的标记。
优点在于,不用将区间的所有值暴力更新,大大提高效率。
在区间修改的一类问题中,我们可以设一个 delta 域,表示该节点需要加上数值 delta。
由于该节点表示的是一个区间,向下访问时,子节点的 delta 需要加上该节点的 delta,
同时该节点的 delta 变为 0。访问叶子节点时,再对该元素的数值加上 delta 即可。
同理,在区间更新(赋值)的一类问题,我们可以设一个 color 域,表示该节点(区间)都被数值 color 覆盖。
向下访问时,子节点的 color 更新成该节点的 color,同时该节点的 color 变为 0。访问叶子节点时,再将该元素修改成 color 即可。
下面的代码就是线段树区间更新的一个例子。
void up(int p)
{
if (!p) return;
s[p] = s[p * 2] + s[p * 2 + 1];
}
void down(int p, int l, int r)
{
if (col[p])
{
int mid = (l + r) / 2;
s[p * 2] = col[p] * (mid - l + 1);
s[p * 2 + 1] = col[p] * (r - mid);
col[p * 2] = col[p * 2 + 1] = col[p];
col[p] = 0;
}
}
void modify(int p, int l, int r, int x, int y, int c)
{
if (x <= l && r <= y)
{
s[p] = (r - l + 1) * c; //仅修改该结点
col[p] = c; //增加标记,子结点待修改
return;
}
down(p, l, r); //下传lazy标记
int mid = (l + r) / 2;
if (x <= mid) modify(p * 2, l, mid, x, y, c);
if (y > mid) modify(p * 2 + 1, mid + 1, r, x, y, c);
up(p);
}
注意到,push_down 一般在访问子节点前执行,起到下传懒惰(延迟)标记的作用。
push_up 在访问完子节点后执行,将两个子区间的信息合并起来,得到该区间的信息。

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
int tree[400005];
int col[400005];
void up(int p)
{
if(!p) return;
tree[p]=tree[p*2]+tree[p*2+1];
}
void down(int p,int l,int r)
{
if(l==r) return;
if(col[p])
{
int mid=(l+r)/2;
tree[p*2]=col[p]*(mid-l+1);
tree[p*2+1]=col[p]*(r-mid);
col[p*2]=col[p*2+1]=col[p];
col[p]=0;
}
}
void modify(int p,int l,int r,int x,int y,int c)
{
if(x<=l&&r<=y)
{
tree[p]=(r-l+1)*c;
col[p]=c;
return;
}
down(p,l,r); //下传lazy标记
int mid=(l+r)/2;
if(x<=mid) modify(p*2,l,mid,x,y,c);
if(y>mid) modify(p*2+1,mid+1,r,x,y,c);
up(p);
}
int n,q,x,y,z;
int main()
{
memset(tree,0,sizeof(tree));
memset(col,0,sizeof(col));
scanf("%d",&n);
scanf("%d",&q);
modify(1,1,n,1,n,1);
for(int i=1;i<=q;i++)
{
scanf("%d%d%d",&x,&y,&z);
modify(1,1,n,x,y,z);
}
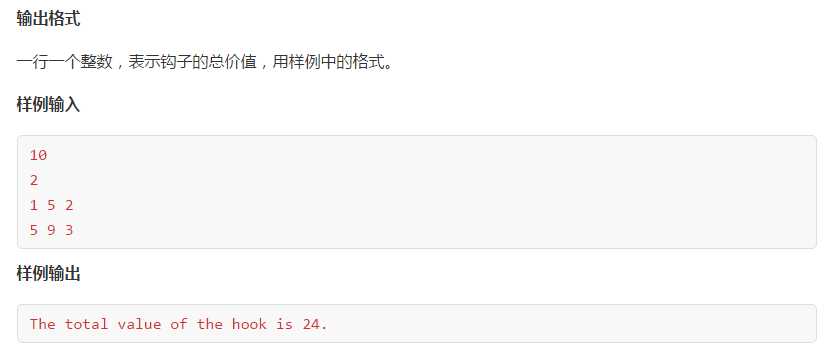
printf("The total value of the hook is %d.\\n",tree[1]);
return 0;
}

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
long long tree[400005];
long long col[400005];
void up(int p)
{
tree[p]=tree[p*2]+tree[p*2+1];
}
void down(int p,int l,int r)
{
if(l==r) return;
if(col[p])
{
int mid=(l+r)/2;
tree[p*2]+=(mid-l+1)*col[p];
tree[p*2+1]+=(r-mid)*col[p];
col[p*2]+=col[p];
col[p*2+1]+=col[p];
col[p]=0;
}
}
void modify(int p,int l,int r,int x,int y,int c)
{
if(x<=l&&r<=y)
{
tree[p]+=(r-l+1)*c;
col[p]+=c;
return;
}
down(p,l,r);
int mid=(l+r)/2;
if(x<=mid)
modify(p*2,l,mid,x,y,c);
if(y>mid)
modify(p*2+1,mid+1,r,x,y,c);
up(p);
}
long long query(int p,int l,int r,int x,int y)
{
down(p,l,r);
if(x<=l&&r<=y)
return tree[p];
int mid=(l+r)/2;
long long ans=0;
if(x<=mid) ans+=query(p*2,l,mid,x,y);
if(y>mid) ans+=query(p*2+1,mid+1,r,x,y);
return ans;
}
int n,q,tmp,a,b,c;
char ch[100];
int main()
{
memset(tree,0,sizeof(tree));
memset(col,0,sizeof(col));
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)
{
scanf("%d",&tmp);
modify(1,1,n,i,i,tmp);
}
for(int i=1;i<=q;i++)
{
scanf("%s",ch);
if(ch[0]==‘C‘)
{
scanf("%d%d%d",&a,&b,&c);
modify(1,1,n,a,b,c);
}
else if(ch[0]==‘Q‘)
{
scanf("%d%d",&a,&b);
printf("%lld\\n",query(1,1,n,a,b));
}
}
return 0;
}

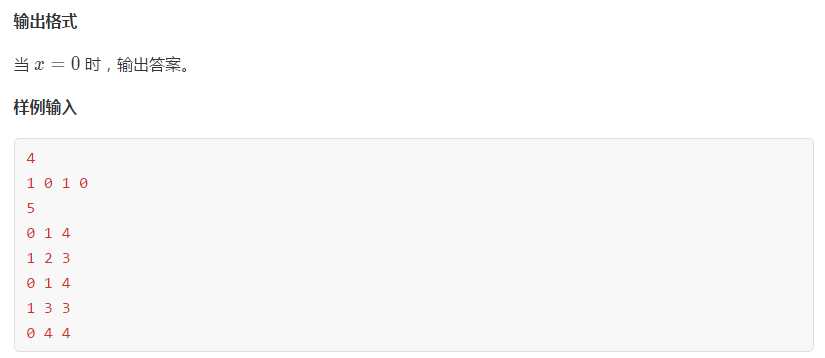


这题不会做,是看了网上的代码
#include<iostream>
#include<stdio.h>
using namespace std;
struct node
{
int lone,lzero;
int rone,rzero;
int tmax0,tmax1;
int flag;//延迟标记,这里要注意下,开始的时候我就是一直错的
int l,r;
int mlen;//节点的区间长度
} p[100001*4];
int a[100001];
int max(int x,int y)
{
return x>y?x:y;
}
int min(int x,int y)
{
return x<y?x:y;
}
void update_info(int n)//向上更新
{
p[n].lone=p[n*2].lone;
if(p[n*2].lone==p[n*2].mlen)//可以合并
p[n].lone+=p[n*2+1].lone;
p[n].lzero=p[n*2].lzero;
if(p[n*2].lzero==p[n*2].mlen)//可以合并
p[n].lzero+=p[n*2+1].lzero;
p[n].rone=p[n*2+1].rone;
if(p[n*2+1].rone==p[n*2+1].mlen)//可以合并
p[n].rone+=p[n*2].rone;
p[n].rzero=p[n*2+1].rzero;
if(p[n*2+1].rzero==p[n*2+1].mlen)//可以合并
p[n].rzero+=p[n*2].rzero;
p[n].tmax0=max(p[n*2].tmax0,p[n*2+1].tmax0);//取左右子树的大者
p[n].tmax0=max(p[n].tmax0,p[n*2].rzero+p[n*2+1].lzero);//和合并之后的比较
p[n].tmax1=max(p[n*2].tmax1,p[n*2+1].tmax1);//同理
p[n].tmax1=max(p[n].tmax1,p[n*2].rone+p[n*2+1].lone);
}
void build(int l,int r,int n)//建树的过程
{
p[n].l=l;
p[n].r=r;
p[n].flag=0;
p[n].mlen=(r-l+1);
if(l==r)
{
if(a[l]==1)
{
p[n].lone=1;
p[n].lzero=0;
p[n].rone=1;
p[n].rzero=0;
p[n].tmax0=0;
p[n].tmax1=1;
}
else
{
p[n].lone=0;
p[n].lzero=1;
p[n].rone=0;
p[n].rzero=1;
p[n].tmax0=1;
p[n].tmax1=0;
}
return ;
}
int mid=(l+r)/2;
build(l,mid,n*2);
build(mid+1,r,n*2+1);
update_info(n);//往上更新
}
void pushdown(int n)//往下更新
{
p[n*2].flag=p[n*2].flag^1;//这里是异或操作注意一下哦
p[n*2+1].flag=p[n*2+1].flag^1;//这里是异或操作注意一下哦
swap(p[n*2].lone,p[n*2].lzero);
swap(p[n*2].rone,p[n*2].rzero);
swap(p[n*2].tmax1,p[n*2].tmax0);
swap(p[n*2+1].lone,p[n*2+1].lzero);
swap(p[n*2+1].rone,p[n*2+1].rzero);
swap(p[n*2+1].tmax1,p[n*2+1].tmax0);
p[n].flag=0;
}
void insert(int x,int y,int n)
{
if(x==p[n].l&&y==p[n].r)
{
swap(p[n].lone,p[n].lzero);
swap(p[n].rzero,p[n].rone);
swap(p[n].tmax1,p[n].tmax0);
p[n].flag=p[n].flag^1;//这里是异或操作注意一下哦
return ;
}
if(p[n].flag==1)
pushdown(n);//往下更新
int mid=(p[n].l+p[n].r)/2;
if(y<=mid)
insert(x,y,n*2);
else if(x>mid)
insert(x,y,n*2+1);
else
{
insert(x,mid,n*2);
insert(mid+1,y,n*2+1);
}
update_info(n);//往上更新
}
int sum(int x,int y,int n)//求连续1的最长的长度
{
if(x==p[n].l&&y==p[n].r)
return p[n].tmax1;
int mid=(p[n].l+p[n].r)/2;
if(p[n].flag==1)
pushdown(n);//往下更新
if(y<=mid)
return sum(x,y,n*2);
else if(x>mid)
return sum(x,y,n*2+1);
else
{
int left=0,right=0,midden=0;
midden=min(mid-x+1,p[n*2].rone)+min(y-mid,p[n*2+1].lone);
left=sum(x,mid,n*2);
right=sum(mid+1,y,n*2+1);
return max(midden,max(left,right));
}
}
int main()
{
int n,m,i,nima,x,y;
while(scanf("%d",&n)!=EOF)
{
for(i=1; i<=n; i++)
scanf("%d",&a[i]);
build(1,n,1);
scanf("%d",&m);
while(m--)
{
scanf("%d%d%d",&nima,&x,&y);
if(nima==1)
insert(x,y,1);
else
printf("%d\\n",sum(x,y,1));
}
}
return 0;
}
以上是关于线段树区间更新的主要内容,如果未能解决你的问题,请参考以下文章
POJ 3468 A Simple Problem with Integers 线段树 区间更新 区间查询
hdoj 1698 Just a Hook 线段树 区间更新
hihoCoder #1078 : 线段树的区间修改(线段树区间更新板子题)