数据结构 ---[实现 线段树(SegmentTree) ]
Posted 小智RE0
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构 ---[实现 线段树(SegmentTree) ]相关的知识,希望对你有一定的参考价值。
1.线段树的概念
首先给你一个数组[1,2,3,4,5];让你把它做成一棵二分搜索树;
做出来大概这样,它是个斜树;高度过高;

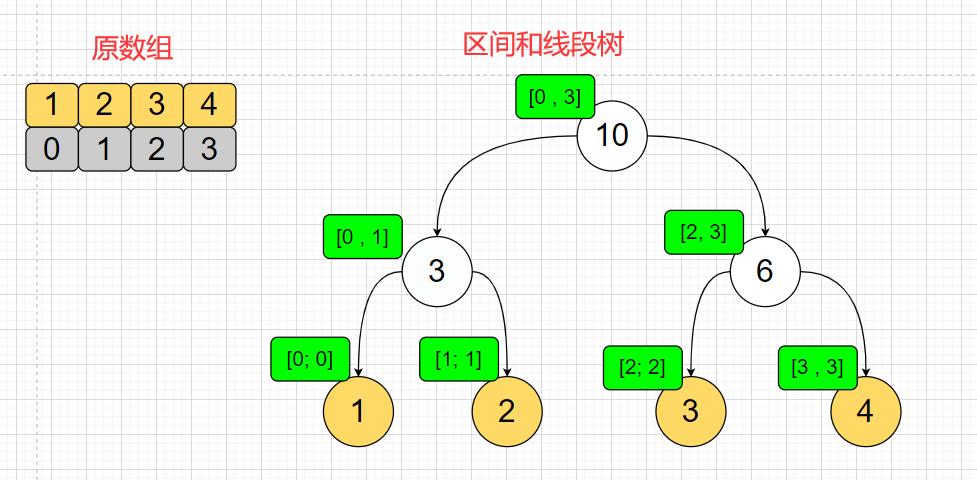
那么,我要是分区间来构建这棵树呢;一个区间一个区间地分化这棵树;然后让区间的和作为树的结点;
并且,注意到数组原来的值都分布在叶子结点上;
左树和右树的高度差不超过1;

可能觉得这个不明显,那用个偶数长度的数组来看看;一样的;原数组的元素分布在叶子结点上;
左树和右树的高度差不超过1;
线段就是一段区间;
线段树不是完全二叉树;它是一棵平衡树;使用线段树可解决区间求和问题,区间求最值问题;
啥是平衡树–>平衡树百度百科
之前也做过关于平衡树的笔记–>平衡二叉搜索树实现
当然这个平衡树也能做区间求和问题;只要定义这个结点的规则即可;
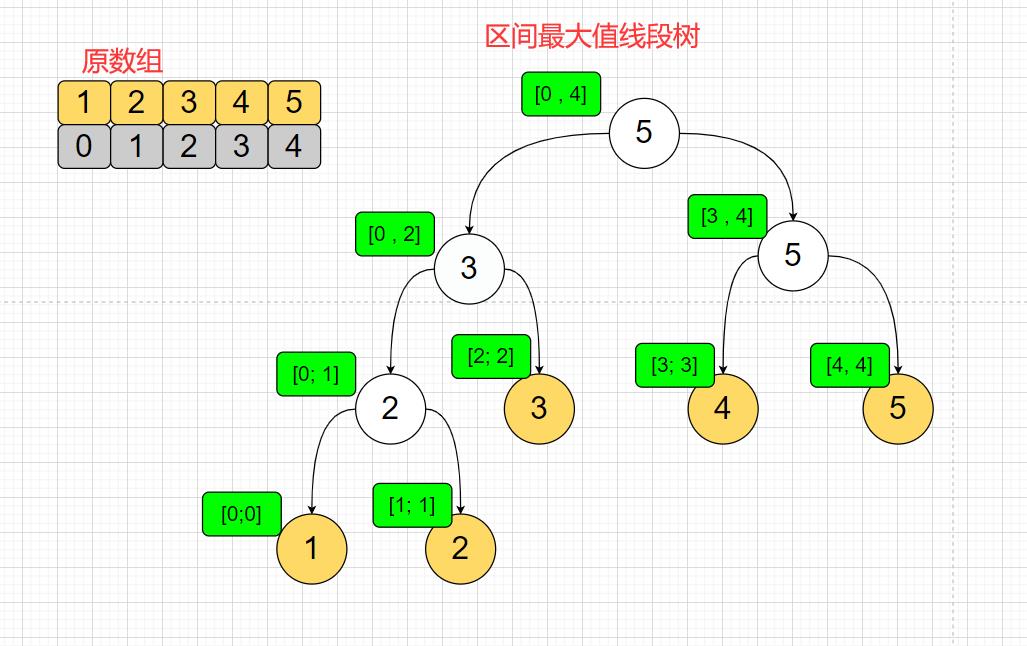
比如我把数组
[1,2,3,4,5]做成区间最大值线段树表示
2.实现线段树,包括 查找指定区间元素 和 更新数组指定位置元素方法
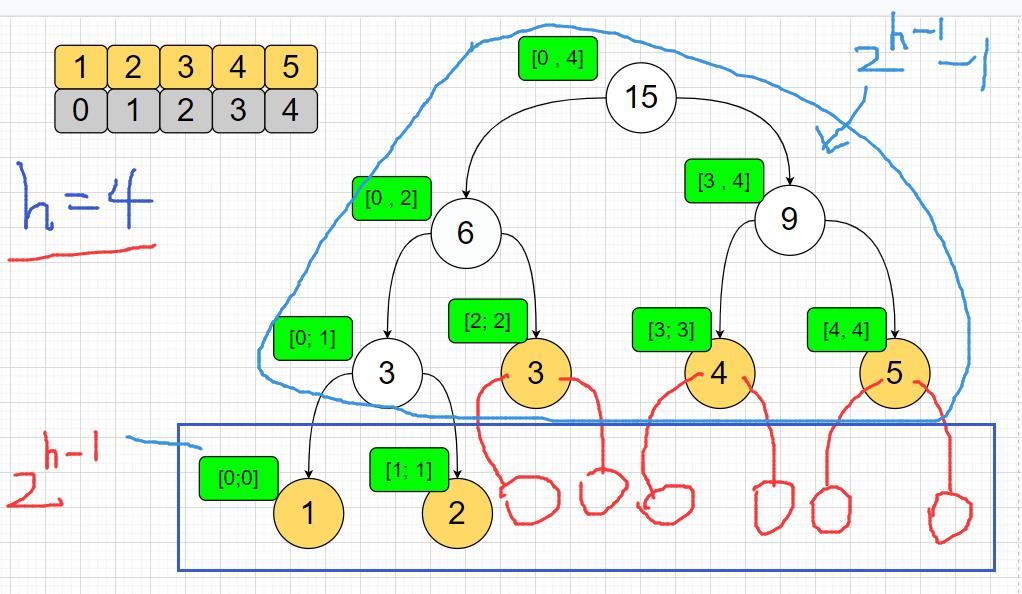
首先,定义线段树的时候,最后是要用数组作为底层存储结构,那么这个数组就得提前确定好长度;
由于左树和右树的高度差不会超过1;
那么假设构建成一棵满二叉树;若树的高度为h,最后一层节点数为2h-1 个节点;
上面的所有结点数量就是2h-1 -1 ;实际这棵树的节点总数就是 2h -1 ;
那么构建线段树的时候,由于底层是数组,宁愿多创建几个空间,也不能少创建空间;
那么数组的长度就是 <= 节点总数;
即 数组长度 = 2h -1
还有,在实现线段树时,这个功能不能写死,要实现动态选择;因为它能解决多种问题,比如区间求和以及区间最值问题;
这时就得考虑使用函数式接口了
什么是函数式接口?有兴趣的可以看看菜鸟教程关于函数式接口的讲解->
该接口有且仅有一个抽象方法;
这里实现之前,我就提前定义好;
/**
* @author by CSDN@小智RE0
* @date 2021-11-28 13:20
*/
//自定义归并接口;作为一个可通用的函数式接口;
public interface Merge<T>
T merge(T a, T b);
由于符合二叉树的规则;实现的话用到递归会多一点;

public class MySegmentTree<T>
//定义的原数组; 线段树数组;
private T[] sourceArr;
private T[] segmentArr;
//通用的函数式接口;
private Merge<T> merge;
//初始化;
public MySegmentTree(T[] arr,Merge<T> merge)
if(arr!=null)
this.merge = merge;
this.sourceArr = Arrays.copyOf(arr,arr.length);
//线段树的高度;
int height = (int) Math.ceil(Math.log(this.sourceArr.length)/Math.log(2)+1);
//线段树的对应数组长度;
int segmentLen = (int) (Math.pow(2,height) -1);
this.segmentArr = (T[]) new Object[segmentLen];
//调用方法构造线段树;
buildSegmentTree(0,this.sourceArr.length-1,0);
/**
* 构造线段树
* @param start 在原数组中的起始索引
* @param end 在原数组中的结束索引
* @param index 在当前线段树的索引 ;[start,end]
*/
private void buildSegmentTree(int start,int end,int index)
//1.确定递归的结束条件,到达最后区间时,比如说[0,0][1,1]...;
if(start == end)
this.segmentArr[index] = this.sourceArr[start];
return;
//进行递归的操作;
//回顾二叉树计算左孩子,右孩子的索引; 当前树的索引由0开始;
int leftIndex = 2*index +1;
int rightIndex = leftIndex+1;
//注意这里计算中值时,需要考虑越界问题,
int middle = start +(end - start)/2;
//这里直接向左向右递归即可;
buildSegmentTree(start,middle,leftIndex);
buildSegmentTree(middle+1,end,rightIndex);
//最后递归调用返回时,按照通用函数式编程的规则进行计算;
this.segmentArr[index] = this.merge.merge(this.segmentArr[leftIndex],this.segmentArr[rightIndex]);
/**
* 打印线段树的方法;
*/
@Override
public String toString()
//首先对数组进行限制判断;
if(this.segmentArr!=null && this.segmentArr.length!=0)
StringBuilder sb = new StringBuilder("[");
Arrays.stream(this.segmentArr).forEach(a->
sb.append(a+",");
);
sb.append("]");
return sb.toString();
else
throw new RuntimeException("the tree is null or error");
测试构建数组区间和线段树;
//测试;
public static void main(String[] args)
Integer[] arr = 1,2,3,4,5;
MySegmentTree<Integer> mst = new MySegmentTree<>(arr,(a,b)->(a+b));
System.out.println(mst);
结果;和分析一致;
[15,6,9,3,3,4,5,1,2,null,null,null,null,null,null,]
测试构建数组区间最大值线段树;只需要更改函数式接口方法的规则即可;
//测试;
public static void main(String[] args)
Integer[] arr = 1,2,3,4,5;
MySegmentTree<Integer> mst = new MySegmentTree<>(arr,(a,b)->(Math.max(a,b)));
System.out.println(mst);
和分析图一致;
[5,3,5,2,3,4,5,1,2,null,null,null,null,null,null,]
(1)在指定区间查找;
比如这里就用在指定区间查找元素和作为案例;
查找的话,可分为三种情况
(1)只往左边方向找值;
比如,这里要查找区间[0, 0]的元素和; 就定为[from:0; to:0]
这里的middle中值,首先计算出是mid=2;发现这个mid已经大于目标区间to:0;
然后肯定向左找啊,再次计算中心点middle,得出mid=1,仍然大于目标区间to:0;
继续向左找;计算得出mid=0,此时等于目标区间to:0;
且此时已经找到指定区间[0,0]的值为1;层层返回调用处即可;

(2)只往右方向查找;
例如需要查找区间[4,4]的元素之和;就定为[from:4; to:4];
先计算得到中点mid=2;小于要查询的区间起点from:4;
那么向右查找,计算此时中点mid=3;小于要查询的区间起点from:4;
此时已找到要查找的区间[4,4]的和为5,层层返回调用处即可;

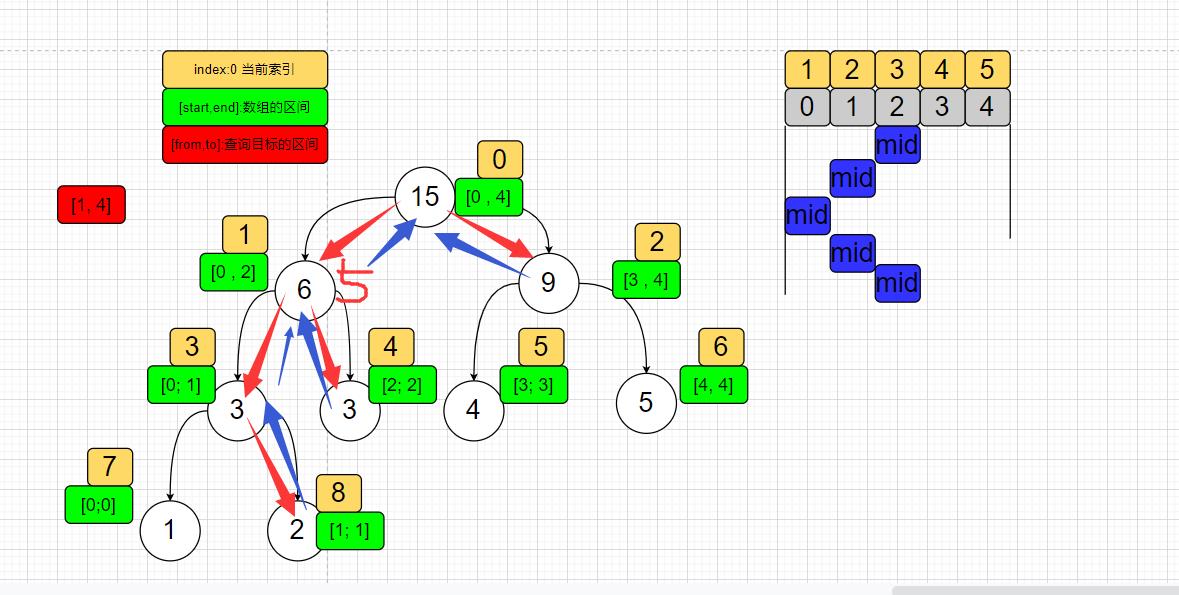
(3)需要向左向右查找;
比如要查询区间[1,4]的元素和;[from:1 ; to:4];
首先计算到的mid值为2,中心点此时在区间之内,就得向左向右找了;
- 先向左找;此时在左边找
区间[1,2];计算mid值为1;此时又得向左向右找;- 先向左找
区间[1,1];计算得出mid值为0,此时from>mid;向右找;
找到区间[1,1],将这个值返回到leftVal左树值为2; - 然后,刚才还要向右找
区间[2,2],正好找到,将这个值返回到rightVal右树值为3;
- 先向左找
- 这一部分的值找完了;返回到调用处,mid为1处,这一块得到的左树值
leftVal为2+3=5; - 然后再向上返回,到之前mid为2处,前面找了左边
区间[1,2], - 在右边区间要找
[3,4],正好找到值为9,那么这块得到的右树值rightVal为9; - 最后再将左右两边的值融合,leftVal与rightVal值融合,得到5+9=14;即
区间[1,4]的元素和为14;
具体实现
/**
* 在指定的区间查找值;
* @param from 目标区间起始索引
* @param to 目标区间结束索引
*/
public T searchSegment(int from,int to)
//这里调用底层的方法实现;
if(this.segmentArr!=null&&this.segmentArr.length!=0)
return searchSegment(0,this.sourceArr.length-1,0,from, to);
else
throw new RuntimeException("the tree is empty or error");
/**
* 找到指定目标区间的值;
* @param start 线段树上节点的起始区间
* @param end 线段树上节点的结束区间
* @param index 线段树上的索引
* @param from 目标区间起始索引
* @param to 目标区间结束索引
* @return 返回指定区间的值;
*/
private T searchSegment(int start, int end,int index, int from, int to)
//首先写出递归结束的条件;
if(start == from && end == to)
return this.segmentArr[index];
//进行递归操作;
//注意分为三个情况,仅向左递归 ;仅向右递归,向左向右都要递归;
int leftIndex = 2*index+1;
int rightIndex = leftIndex+1;
int middle = start+(end-start)/2;
if(to <= middle)
//仅向左;
return searchSegment(start,middle,leftIndex,from,to);
else if(from > middle)
//仅向右;
return searchSegment(middle+1,end,rightIndex,from,to);
else
//向左向右;
T leftVal= searchSegment(start,middle,leftIndex,from,middle);
T rightVal= searchSegment(middle+1,end,rightIndex,middle+1,to);
return this.merge.merge(leftVal,rightVal);
测试使用
//测试;
public static void main(String[] args)
Integer[] arr = 1,2,3,4,5;
MySegmentTree<Integer> mst = new MySegmentTree<>(arr,(a,b)->(a+b));
System.out.println("区间[1,4]的和为"+mst.searchSegment(1,4));
//区间[1,4]的和为14
(2)更新指定位置的值;
比如要将数组索引位置为3的元素4修改为10;

在数组中直接更改即可,主要是在线段树中需要更改时,要先去找这个叶子节点;在找的时候,
其中还要计算中心点;
由于这个中心点当时构建的时候就默认向下取整的,
所以要是中心点的值大于等于目标位置时,向左边找,中心点要是小于目标位置时,向右边查找;
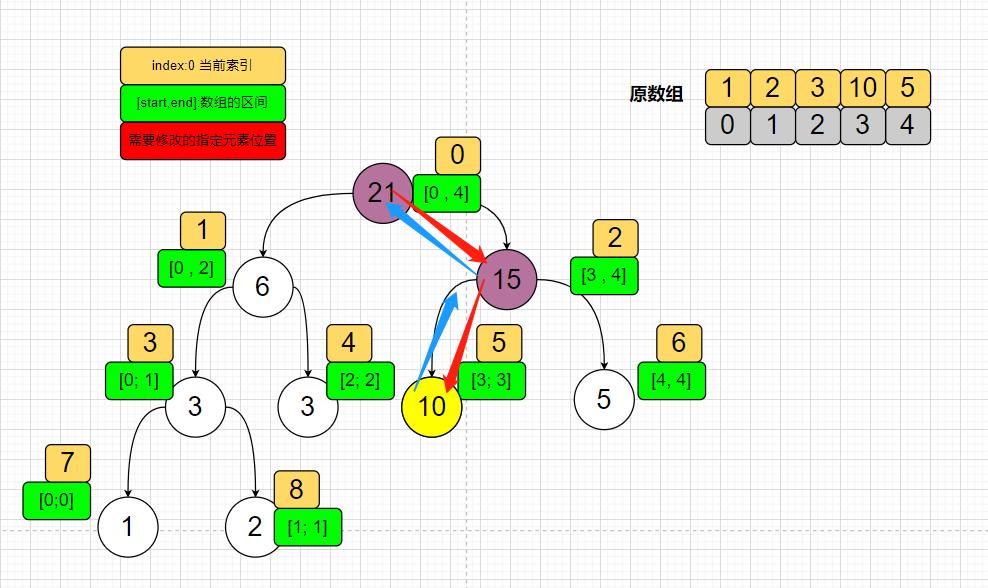
这里实现的话比较简单
/**
* 更改原数组指定位置的元素为指定值;
* @param position 原数组的指定位置
* @param val 指定元素
*/
public void updateItem(int position,T val)
//线段树异常;
if(this.sourceArr==null || this.sourceArr.length==0)
throw new RuntimeException("the tree is null");
//位置参数错误;
if(position<0|| position >= this.sourceArr.length)
throw new RuntimeException("Positional parameter error");
//调用方法;
updateItem(0,this.sourceArr.length-1,0,position,val);
/**
* 修改原数组指定位置的元素为指定值;
* @param start 原数组指定区间起始索引;
* @param end 原数组指定区间结束索引;
* @param index 线段树的索引;
* @param position 要修改的指定位置;
* @param val 要修改的值;
*/
private void updateItem(int start, int end, int index, int position, T val)
//1.递归终止的条件;
if(start == end && start == position)
this.sourceArr[position] = this.segmentArr[index] = val;
return;
//递归操作;
int leftIndex = 2*index+1;
int rightIndex = leftIndex+1;
int middle = start + (end-start)/2;
//这边修改的话,就递归两个方向; 指定位置在大于中心点,则右边; 因为当时中心点是向下取整的;
if(position > middle)
updateItem(middle+1,end,rightIndex,position,val);
else
updateItem(start,middle,leftIndex,position,val);
//最终融合结果;
this.segmentArr[index] = this.merge.merge(this.segmentArr[leftIndex],this.segmentArr[rightIndex]);
测试使用
//测试;
public static void main(String[] args)
Integer[] arr = 1,2,3,4,5;
MySegmentTree<Integer> mst = new MySegmentTree<>(arr,(a,b)->(a+b));
//System.out.println("----更改元素4--");
mst.updateItem(3,10);
System.out.println(mst);
测试结果,和分析的一致
[21,6,15,3,3,10,5,1,2,null,null,null,null,null,null,]
线段树代码总结
/**
* @author by CSDN@小智RE0
* @date 2021-11-28 10:53
*/
public class MySegmentTree<T>
//定义的原数组; 线段树数组;
private T[] sourceArr;
private T[] segmentArr;
//通用的函数式接口;
private Merge<T> merge;
//初始化;
public MySegmentTree(T[] arr,Merge<T> merge)
if(arr!=null)
this.merge = merge;
this.sourceArr = Arrays.copyOf(arr,arr.length);
//线段树的高度;
int height = (int) Math.ceil(Math.log(this.sourceArr.length)/Math.log(2)+1);
//线段树的对应数组长度;
int segmentLen = (int) (Math.pow(2,height) -1);
this.segmentArr = (T[]) new Object[segmentLen];
//调用方法构造线段树;
buildSegmentTree(0,this.sourceArr.length-1,0);
/**
* 构造线段树
* @param start 在原数组中的起始索引
* @param end 在原数组中的结束索引
* @param index 在当前线段树的索引 ;[start,end]
*/
private void buildSegmentTree(int start,int end,int index)
//1.确定递归的结束条件,到达最后区间时,比如说[0,0][1,1]...;
if(start == end)
this.segmentArr[index] = this.sourceArr[start];
return;
//进行递归的操作;
//回顾二叉树计算左孩子,右孩子的索引; 当前树的索引由0开始;
int leftIndex = 2*index +1;
int rightIndex = leftIndex+1;
//注意这里计算中值时,需要考虑越界问题,
int middle = start 以上是关于数据结构 ---[实现 线段树(SegmentTree) ]的主要内容,如果未能解决你的问题,请参考以下文章