线段树单点更新

Posted 2020-09-20

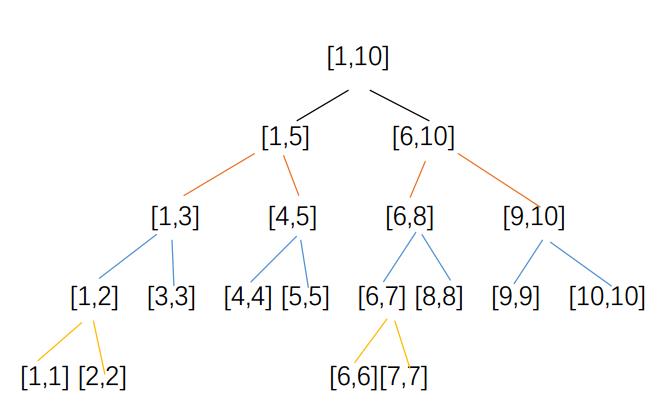
线段树，就是一棵由线段构成的二叉树，每个结点都代表一条线段 [a, b]。

非叶子的结点所对应的线段都有两个子结点，左儿子代表的线段为 [a,?(a+b)/2??]，右儿子代表的线段为 [(a+b)/2+1,b]。

使用线段树这一数据结构，可以查找一个连续区间中节点的信息，也可以修改一个连续区间中结点的信息。换句话说，它将优化区间操作的复杂度。

例

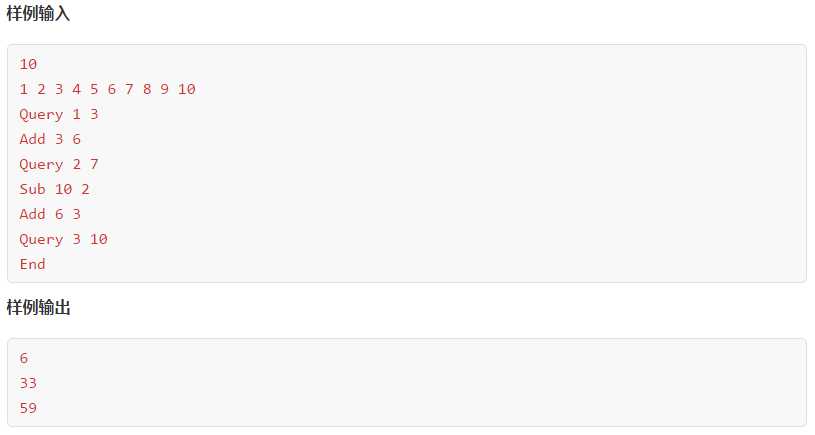
初始数组 A_1,A_2,A_3...A_n?? ，需要支持以下操作：

1 x v 修改操作，对第 x 个元素加上 v，即 A_x = A_x + v。

2 x y 查询操作， 询问区间和，即 .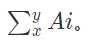

修改

n = 10, x = 3

根结点 [1, 10]，sum(1, 10) += v

左儿子是 [1, 5]，右儿子是 [6, 10]，我们选择左儿子。

当前结点 [1, 5]，sum(1, 5) += v

左儿子是 [1, 3]，右儿子是 [4, 5]，我们选择左儿子。

当前结点 [1, 3]，sum(1, 3) += v

左儿子是 [1, 2]，右儿子是 [3, 3]，我们选择右儿子。

当前结点 [3, 3]，sum(3, 3) += v。

长度范围为 [1, n] 的一棵线段树的深度为 log (n) + 1。

对照图示，我们若修改第 3 个元素，在线段树上，恰好修改 [1,10],[1,5],[1,3],[3,3] 这些区间。

由二叉树的性质可知，单次修改的区间数量是 log 级别的，单次修改的复杂度是 O(logn) 。

void modify(int p, int l, int r, int x, int v)
{
    s[p] += v;
    if (l == r) return; //叶结点则退出
    int mid = (l + r) / 2;
    if (x <= mid) //判断x在左儿子还是右儿子
        modify(p * 2, l, mid, x, v);
    else
        modify(p * 2 + 1, mid + 1, r, x, v);
}

 

也可以 push_up：把儿子结点的信息更新到父亲结点

void up(int p)
{
    s[p] = s[p * 2] + s[p * 2 + 1];
}

void modify(int p, int l, int r, int x, int v)
{
    if (l == r)
    {
        s[p] += v;
        return;
    }
    int mid = (l + r) / 2;
    if (x <= mid)
        modify(p * 2, l, mid, x, v);
    else
        modify(p * 2 + 1, mid + 1, r, x, v);
    up(p);
}

 

查询

查询的区间 [x, y] 划分为线段树上的结点，然后将这些结点代表的区间合并起来得到所需信息。

n=10,x=3,y=6 ，即我们需要求出 A_3+A_4+A_5+A_6。

而区间 [3,6] 的信息，刚好由线段树上区间 [3, 3]，[4, 5]，[6, 6] 合并得到。

线段树上每层的结点最多会被选取 2 个，一共选取的结点数也是 O(logn) 的，因此查询的时间复杂度也是 )O(logn)。

int query(int p, int l, int r, int x, int y)
{
    if (x <= l && r <= y) return s[p];//若该结点被查询区间包含
    int mid = (l + r) / 2, res = 0;
    if (x <= mid) res += query(p * 2, l, mid, x, y);
    if (y > mid) res += query(p * 2 + 1, mid + 1, r, x, y);
    return res;
}

 

#include<iostream>
#include<stdio.h>
#include<vector>
#include<queue>
#include<algorithm>
#include<memory.h>
#include<string.h>
#include<cmath>
#include<map>
#include<set>
#define INF 0x3f3f3f3f
#define PII pair<int,int>
#define MOD 1000000000
#define MAX_N 1000
using namespace std;
int n,m,w,x,y,tmp;
int tree[200005];
int arr[50005];
void modify(int p,int l,int r,int x,int v)
{
    tree[p]+=v;
    if(l==r) return;
    int mid=(l+r)/2;
    if(x<=mid)
        modify(2*p,l,mid,x,v);
    else
        modify(2*p+1,mid+1,r,x,v);
}

int query(int p,int l,int r,int x,int y)
{
    if(x<=l&&r<=y) return tree[p];
    int mid=(l+r)/2,res=0;
    if(x<=mid) res+=query(p*2,l,mid,x,y);
    if(y>mid) res+=query(p*2+1,mid+1,r,x,y);
    return res;
}

void insert(int p,int l,int r,int k,int x)
{
    if(l==k&&r==k)
    {
        tree[p]+=x;
        return;
    }
    int mid=(l+r)/2;
    if(k<=mid)
        insert(p*2,l,mid,k,x);
    else insert(p*2+1,mid+1,r,k,x);
    tree[p]+=x;
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&tmp);
        insert(1,1,n,i,tmp);
    }

    char op[25];
    while(true)
    {
        scanf("%s",&op);
        if(op[0]==‘E‘) break;
        scanf("%d%d",&x,&y);
        if(op[0]==‘A‘)
        {
            modify(1,1,n,x,y);
        }
        else if(op[0]==‘S‘)
        {
            modify(1,1,n,x,-y);
        }
        else if(op[0]==‘Q‘)
        {
            printf("%d\\n",query(1,1,n,x,y));
        }
    }
    return 0;
}

 

#include<iostream>
#include<stdio.h>
using namespace std;
int n,m,tmp,a,b;
int arr[200005];
int tree[800005];
void up(int p)
{
    tree[p]=max(tree[p*2],tree[p*2+1]);
}
void modify(int p,int l,int r,int x,int v)
{
    if(l==r)
    {
        tree[p]=v;
        return;
    }
    tree[p]=max(tree[p],v);
    int mid=(l+r)/2;
    if(x<=mid)
        modify(p*2,l,mid,x,v);
    else
        modify(p*2+1,mid+1,r,x,v);
    up(p);
}
void insert(int p,int l,int r,int x,int v)
{

}
int query(int p,int l,int r,int x,int y)
{
    int maxx=-1;
    if(x<=l&&y>=r) return tree[p];
    int mid=(l+r)/2;
    if(x<=mid)
        maxx=max(maxx,query(p*2,l,mid,x,y));
    if(y>mid)
        maxx=max(maxx,query(p*2+1,mid+1,r,x,y));
    return maxx;
}
int main()
{
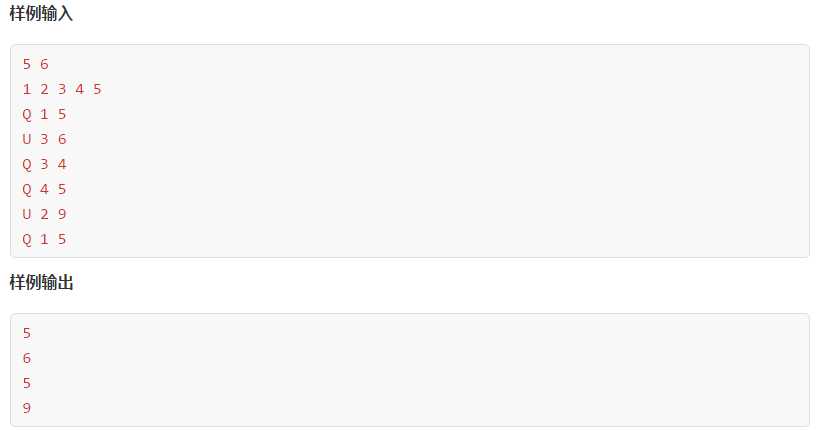
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&tmp);
        modify(1,1,n,i,tmp);
    }
    char c;
    for(int i=1;i<=m;i++)
    {
        scanf(" %c%d%d",&c,&a,&b);
        if(c==‘Q‘)
            printf("%d\\n",query(1,1,n,a,b));
        else
            modify(1,1,n,a,b);
    }

    return 0;
}

 

#include<iostream>
#include<stdio.h>
#include<memory.h>
using namespace std;
int tree[800005];
int h,w,n,tmp;
void up(int p)
{
    tree[p]=min(tree[p*2],tree[p*2+1]);
}
void modify(int p,int l,int r,int x,int v)
{
    if(l==r)
    {
        tree[p]+=v;
        return;
    }
    int mid=(l+r)/2;
    if(x<=mid)
        modify(p*2,l,mid,x,v);
    else
        modify(p*2+1,mid+1,r,x,v);
    up(p);
}
int query(int p,int l,int r,int value)
{
    if(tree[p]>value)
    {
        return -1;
    }
    if(l==r)
    {
        return l;
    }
    int mid=(l+r)/2;
    if(tree[p*2]<=value)
        return query(p*2,l,mid,value);
    else
        return query(p*2+1,mid+1,r,value);
}
int main()
{
    memset(tree,0,sizeof(tree));
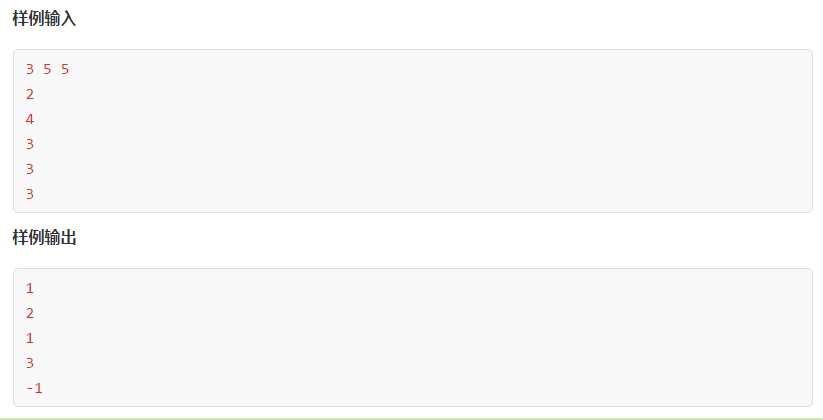
    scanf("%d%d%d",&h,&w,&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&tmp);
        //找到已用长度<=w-tmp的最前行
        int value=w-tmp;
        if(value<0) printf("-1\\n");
        else
        {
            int pos=query(1,1,n,value);
            if(pos>h) printf("-1\\n");
            else printf("%d\\n",pos);
            if(pos!=-1&&pos<=h)
                modify(1,1,n,pos,tmp);
        }
    }
    return 0;
}