对数几率回归法（梯度下降法，随机梯度下降与牛顿法）与线性判别法(LDA)

Posted 2020-09-17 视野

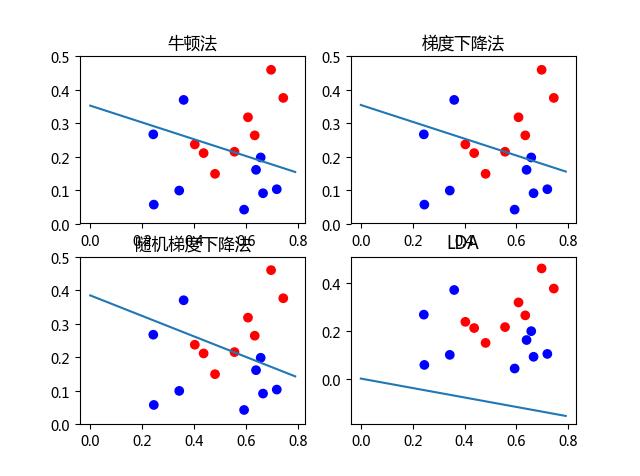
　　本文主要使用了对数几率回归法与线性判别法（ＬＤＡ）对数据集（西瓜３.０）进行分类。其中在对数几率回归法中，求解最优权重Ｗ时，分别使用梯度下降法，随机梯度下降与牛顿法。

代码如下：

  1 #!/usr/bin/env python
  2 # -*- coding: utf-8 -*-
  3 # @Date    : 2017-05-09 15:03:50
  4 # @Author  : whb ([e-mail])
  5 # @Link    : ${link}
  6 # @Version : $Id$
  7 
  8 import numpy as p
  9 import matplotlib.pyplot as plt
 10 import pandas as pd
 11 import random
 12 from scipy.linalg import solve,inv
 13 
 14 def read_data(file_name):
 15     train_data = pd.read_excel(file_name)  # 得到一个数据框（每一列代表一个实例）
 16     return[list(train_data.ix[0]), list(train_data.ix[1]), list(train_data.ix[2]), list(train_data.ix[3])]
 17 ###算法##
 18 # 1 对数几率回归
 19 def func(x, y, w):
 20     #\'x为样本，y为样本类别，w为权重+偏向\'
 21     n = len(x[0])  # 训练集个数
 22     m = len(x)  # 每个实例的属性个数 m-1
 23     result = 0
 24     for i in xrange(n):
 25         s = 0
 26         for j in xrange(m):
 27             s += x[j][i] * w[j]
 28         result += -y[i] * (s) + p.log(1 + p.exp(s))
 29     return result
 30 
 31 
 32 def p1(x, w):
 33     # 后验概率估计
 34     wx = 0
 35     for i in xrange(len(x)):
 36         wx += w[i] * x[i]
 37     return p.exp(wx) / (1 + p.exp(wx))
 38 
 39 
 40 def dfunc(x, y, w):
 41     # 一阶导数
 42     df = p.zeros(len(x))
 43     for i in xrange(len(x[0])):
 44         df += x[:, i] * (y[i] - p1(x[:, i], w))
 45     return -df
 46 
 47 
 48 def d2func(x, y, w):
 49     # 二阶导数
 50     n = len(x[0])
 51     d2f = p.zeros((n, n))
 52     for i in xrange(len(x[0])):
 53         d2f[i][i] = (1 - p1(x[:, i], w)) * p1(x[:, i], w)
 54     return p.mat(x) * p.mat(d2f) * p.mat(x.transpose())
 55 
 56 
 57 # 牛顿法
 58 def newtown(x, y, w, error, n):
 59     i = 1
 60     while i < n:
 61         d1 = dfunc(x, y, w)
 62         if p.dot(d1, d1) < error:
 63             print \'牛顿法： 迭代 \' + str(i) + \'步：w=\', w
 64             return w
 65             break
 66         w = w - solve(d2func(x, y, w), dfunc(x, y, w))
 67         i += 1
 68     
 69 
 70 # 梯度下降法
 71 def gradienet_down(x, y, w, error, n):
 72     i = 1
 73     h = 0.1
 74     while i < n:
 75         start1 = func(x, y, w)
 76         df = dfunc(x, y, w)
 77         w = w - h * df
 78         start2 = func(x, y, w)
 79         if abs(start1 - start2) < error:
 80             print \'梯度下降法：迭代 \' + str(i) + \'步：w=\', w
 81             return w
 82             break
 83         i += 1
 84     
 85 
 86 #随机梯度下降算法
 87 def SGD(x, y, w, error, n):
 88     i = 1
 89     h = 0.1
 90     while i < n:
 91 
 92         start1 = func(x, y, w)
 93         
 94         x_set=range(17)
 95         random.shuffle(x_set) #随机洗牌
 96         for k in  x_set: #只使用一个样本更新权重
 97             df = -x[:, k] * (y[k] - p1(x[:, k], w))
 98             w = w - h * df
 99         start2 = func(x, y, w)
100         if abs(start1 - start2) < error:
101             print \'随机梯度法： 迭代\' + str(i) + \'步：w=\', w
102             return w
103             break
104         i += 1
105     
106 
107 
108 
109 #LDA线性判别法
110 def LDA(x,y):
111     x=p.mat(x[:2])
112     u0=p.zeros((2,1))
113     m0=0
114     u1=p.zeros((2,1))
115     m1=0
116     for  j in xrange(len(y)):
117         if y[j]==1:
118             u1 += x[:,j]
119             m1 +=1
120         else:
121             u0 += x[:,j]
122             m0 +=1
123     u0=u0/m0 #均值
124     u1=u1/m1      
125     sum_=p.zeros((2,2)) #类内方差矩阵。
126     for i in xrange(17):
127         if y[i]==1:
128             sum_ += (x[:,i]-u1)*(p.mat(x[:,i]-u1).T)
129         else:
130             sum_ += (x[:,i]-u0)*(p.mat(x[:,i]-u0).T)
131     return inv(sum_)*p.mat(u0-u1)
132 
133 #可视化
134 def result_plot(x,y,w_min):
135     x1 = p.arange(0, 0.8, 0.01)
136     y1 = [-(w_min[2] + w_min[0] * x1[k]) / w_min[1] for k in xrange(len(x1))]
137     color = [\'r\'] * y.count(1.) + [\'b\'] * y.count(0.)
138     plt.scatter(x[0], x[1], c=color)
139     plt.plot(x1, y1)
140 
141 
142 if __name__ == \'__main__\':
143     file_name = \'xigua.xls\'
144     data = read_data(file_name)
145     x = data[:3]  # 各实例的属性值
146     x = p.array(x)
147     y = data[-1] # 类别标记
148     w = [1, 1, 1]  # 初始值
149     error = 0.0001  # 误差
150     n = 1000  # 迭代步数
151 
152     w_min=newtown(x,y,w,error,n)
153 
154     w_min1= gradienet_down(x, y, w, error, n)
155 
156     w_min11=SGD(x, y, w, error, n)
157   
158     w_min2=LDA(x, y)
159     
160     w_min2=[w_min2[0,0],w_min2[1,0],0]
161     # 可视化
162     plt.figure(1)
163     plt.subplot(221)
164     result_plot(x,y,w_min)
165     plt.title(u\'牛顿法\')
166     plt.subplot(222)
167     result_plot(x,y,w_min1)
168     plt.title(u\'梯度下降法\')
169     plt.subplot(223)
170     result_plot(x,y,w_min11)
171     plt.title(u\'随机梯度下降法\')
172     plt.subplot(224)
173     result_plot(x,y,w_min2)
174     plt.title(u\'LDA\')
175     plt.show()
176     

View Code

结果：

牛顿法： 迭代 5步：w= [ 3.14453235 12.52792035 -4.42024654]
梯度下降法：迭代 838步：w= [ 2.80637226 11.14036869 -3.95330427]
随机梯度法： 迭代182步：w= [ 1.84669379 6.02658819 -2.31718771]