牛顿法梯度下降法与拟牛顿法

Posted 2023-04-08 小何才露尖尖角

牛顿法、梯度下降法与拟牛顿法

• 0 引言
• 1 关于泰勒展开式
• • 1.1 原理
  • 1.2 例子
• 2 牛顿法
• • 2.1 x 为一维
  • 2.2 x 为多维
• 3 梯度下降法
• 4 拟牛顿法
• • 4.1 拟牛顿条件
  • 4.2 DFP 算法
  • 4.3 BFGS 算法
  • 4.4 L-BFGS 算法

0 引言

机器学习中在求解非线性优化问题时，常用的是梯度下降法和拟牛顿法，梯度下降法和拟牛顿法都是牛顿法的一种简化

牛顿法是在一个初始极小值点做二阶泰勒展开，然后对二阶泰勒展开式求极值点，通过迭代的方式逼近原函数极值点

在牛顿法迭代公式中，需要求二阶导数，而梯度下降法将二阶导数简化为一个固定正数方便求解

拟牛顿法也是在求解过程中做了一些简化，不用直接求二阶导数矩阵和它的逆

1 关于泰勒展开式

1.1 原理

如果我们有一个复杂函数 $f(x)$, 对这个复杂函数我们想使用 n 次多项式（多项式具有好计算，易求导，且好积分等一系列的优良性质）去拟合这个函数，这时就可以对 $f(x)$进行泰勒展开，求某一点 $x_0$附近的 n 次多项式：

注意：
n 次多项式只是在 $x_0$ 较小的邻域内能较好拟合 $f(x)$，也就是说，泰勒展开式其实是一种局部近似的方法，只近似 $x=x_0$那一点的函数性

1.2 例子

现在要求 $f(x)=cos(x)$ 在 $x_0=0$ 处的二阶泰勒展开，因为我们去掉了高阶项，所以只是近似

直接套用公式
$f(x_0)=f(0)=cos(0)=1$
$f^{\prime }(x_0)=f^{\prime }(0)=-sin(0)=0$
$f^{\prime \prime }(x_0)=f^{\prime \prime }(0)=-cos(0)=-1$
所以展开后的公式为
$$f(x)\approx f(x_0)+f^{\prime }(x_0)\ast x+f^{\prime \prime }(x_0)\ast x^2/2=1-0.5\ast x^2$$

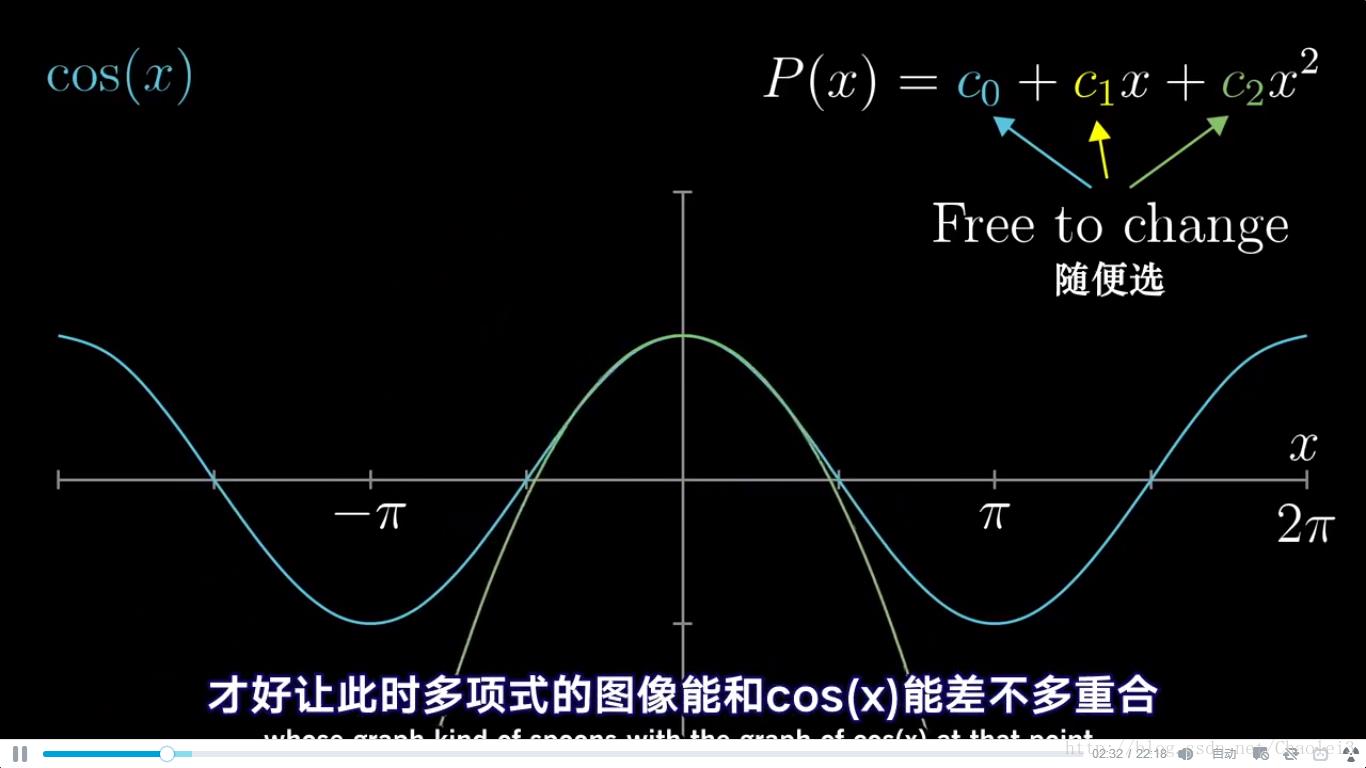
从下方运行程序可以看出，离展开点越近的点，拟合程度越高，越远的点，越离谱

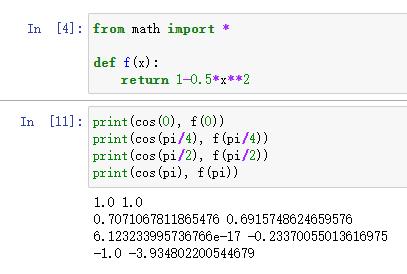
2 牛顿法

2.1 x 为一维

现在假设我们有目标函数 $f(x)$，我们希望求此函数的极小值，牛顿法的基本思想是：随机找到一个点设为当前极值点 $x_k$，在这个点对 $f(x)$ 做二次泰勒展开，进而找到极小点的下一个估计值。在 $x_k$ 附近的二阶泰勒展开为：

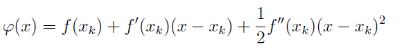
现在想求 $\phi (x)$ 的极值点，由极值的必要条件可知，$\phi (x)$ 应满足导数为 0，即：
$${\phi }^{\prime }(x)=0$$
即
$${\phi }^{\prime }(x)=f^{\prime }(x_k)+f^{\prime \prime }(x_k)(x-x_k)=0$$
这样就可以求得 x 的值
$$x=x_k-\frac{f^{\prime }(x_k)}{f^{\prime \prime }(x_k)}$$
于是给定初始值 $x_0$,就可以通过迭代的方式逼近$f(x)$的极值点：
$$x_{k+1}=x_k-\frac{f^{\prime }(x_k)}{f^{\prime \prime }(x_k)}$$

如下图，首先在 $x_n$ 处泰勒展开，得到$f(x)$ 的近似函数 $g_n(x)$ ，求得 $g_n(x)$ 的极值点 $x_{n+1}$

随后在 $x_{n+1}$ 出泰勒展开，得到$g_{n+1}(x)$ 函数，继续求$g_{n+1}(x)$ 的极值点

一直迭代最后就会逼近 $f(x)$ 的极值点

2.2 x 为多维

上面讨论的是参数 x 为一维的情况，当 x 有多维时，二阶泰勒展开式可以做推广，此时：
$$\phi (x)\&\#$$

无约束优化问题中牛顿法与拟牛顿法四种迭代方法的matlab实现

文章目录

• • • 1. 无约束优化问题的解法
    • 2. Matlab实现
    • • 2.1. Newton’s method(牛顿法)
      • 2.2. Levenberg-Marquardt’s method(LM)
      • 2.3. Broyden-Fletcher-Goldfarb-Shanno’s method(BFGS)
      • 2.4. Davidon-Fletcher-Powell’s method(DFP)

1. 无约束优化问题的解法

在无约束优化问题中，有四种经典的迭代优化方法：Newton’s method(牛顿法)、Levenberg-Marquardt’s method(非线性最小二乘法,LM)、Broyden-Fletcher-Goldfarb-Shanno’s method(BFGS)、Davidon-Fletcher-Powell’s method(DFP)。

2. Matlab实现

假设有如下无约束优化问题：$$f(x_1,x_2)=(x_1-3{)}^4+(x_1-3x_2{)}^2$$为了方便四种算法的比较，我们统一设置初始迭代点为 $x_0=[0,0{]}^T$ ，则初始海森矩阵为：$$H_0=\left(\begin{array}{ccc}110& -6& \\ -6& 18& \end{array}\right)$$

上述优化问题用matlab代码表示为：

syms x1; % 变量x1
syms x2; % 变量x2
f = (x1 - 3).^4 + (x1 - 3*x2).^2; $ 函数表达
x0=[0 0]'; % 初始迭代点
H0=[110 -6;-6 18]; % 初始海森矩阵
m=2; % 变量个数
k=30; % 迭代次数

该函数的最优$X=(x_1,x_2)$以及$f(x_1,x_2)$应该为：$$x_1=3,x_2=1$$$$f(x_1,x_2)=0$$

下面展示一下如何用Matlab实现对函数的优化：

2.1. Newton’s method(牛顿法)

牛顿法的迭代公式为：$$x_{k+1}=x_k-H^{-1}(x_k)\nabla f(x_k)$$matlab实现函数实现为：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%文件名:Newton.m
%
%f表示函数表达式
%H0表示初始的海森矩阵
%x0表示初始的迭代点 为列向量
%m表示变量的个数
%k表示迭代次数
%X存储每次迭代的x,F为函数值，G为每次的梯度，H为海森阵，HN为海森矩阵的逆
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function[X, H, F, G,HN] = Newton(f,H0,x0,m,k)
    x1 = sym('x',[1,m]); % [x1, x2]
    %f = (x1(1) - 3)^4 + (x1(1) - 3*x1(2))^2;
    c = num2cell(x1); % c=变量[x1, x2]
    g = sym('x',[m,1]); % [x1, x2]^T
    
    X = zeros(m, k+1); % x1、x2的迭代值
    H = zeros( m, m, k+1); % hessian的迭代值
    F = zeros(1, k+1); % function的迭代值
    G = zeros(m, k+1); % function‘的迭代值
    HN = zeros( m, m, k+1); % hessian的逆阵的迭代值
    
    H(:,:,1) = H0; % hessian初始化
    HN(:,:,1) = inv(H0); % hessian逆初始化
    X(:,1) = x0; % X(x1, x2)初始化
    F(1,1) = subs(f, c, X(:,1)'); % 初始X值赋予F
    h = hessian(f,x1);%求海森矩阵
    
    for n = 1:m % f对x1、x2分别求偏导
        g(n) = diff(f,x1(n));
    end
     G(:,1) = subs(g,c,X(:,1)'); % 初始X导赋予G
     
     % 迭代
    for n = 1:k
        X(:,n+1) = X(:,n) - (H(:,:,n))\\G(:,n);
        F(1,n+1) = subs(f,c,X(:,n+1)'); 
        G(:,n+1) = subs(g,c,X(:,n+1)');
        H(:,:,n+1) = subs(h,c,X(:,n+1)');
        HN(:,:,n+1) = inv(H(:,:,n+1));
    end
end

执行matlab代码：

[X, H, F, G, HN] = Newton(f,H0,x0,m,k);

即可得到优化结果，下表是迭代次数 k 分别为：0、1、2、3时的输出值：

$k$	$x_k$	$f(x_k)$	$\nabla f(x_k)$	$H(x_k)$
0	$(0,0)$	81	$(-108,0)$	$\left(\begin{array}{ccc}110& -6& \\ -6& 18& \end{array}\right)$
1	$(1,0.3333)$	16	$(-32,0)$	( 50 − 6 − 6 18 ) \\beginpmatrix50 & -6 &\\\\-6 & 18 &\\\\\\endpmatrix (50以上是关于牛顿法梯度下降法与拟牛顿法的主要内容，如果未能解决你的问题，请参考以下文章 牛顿法与拟牛顿法 拟牛顿条件 拟牛顿法之BFGS 牛顿法与拟牛顿法 梯度下降之模拟退火梯度下降之学习计划牛顿法拟牛顿法共轭梯度法 最小二乘法+牛顿法+拟牛顿法+梯度下降法+梯度上升法+共轭梯度法 拟牛顿法的DFP方法