斯坦福大学公开课：监督学习应用，梯度下降

Posted 2020-09-17 橙子牛奶糖

监督学习应用例子：以房屋大小和价格为例，本次采用47个样本。

m: training examples,训练样本集

x: "input",variables/features变量，x为输入变量，在本次例子中，表示房屋大小

y: "output", variable/"target" variable，y为输出变量，在本次例子中，表示房屋价格

（x,y）: training examples 表示训练样本

监督学习的流程如下（以房子为例）：

                                        training set（训练集）

                                                ↓

                                    learning algorithm（学习算法）

                                                ↓

new living area(新的房子大小)   →  h（假设与之相关的函数）→estimate price（根据h函数评估房子价格）

对于函数h(x)=h_θ(x)=θ₀+θ₁x₁+θ₂x₂

其中x₁表示房子大小，x₂表示卧室数量；

h_θ(x)表示特征向量x预测的价格；

因此公式会转为为：

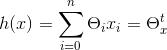
n表示特征向量的个数;

在本例中，特征向量只有2，一个是房子大小，另外一个是卧室数量，因此n为2，如下公式所示，

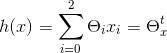
J(θ)表示的是真实值和预测值之间的差距。利用的原理是最小二乘法。

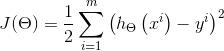
对于J(θ),我们要做的就是使J(θ)最小化，J(θ)越小，说明我们预测的结果越准确。

梯度下降法的原理是通过多次迭代，当J(θ)不再发生很大变化，说明已经收敛了。

随机梯度下降：当样本量很大时，比如几十亿的训练样本量。这个时候采用随机梯度下降法比较合适。可以有效节省时间。但是随机梯度下降法不会精确收敛到全局的最小值。也就是意味着，你在下降过程中，可能在全局最小值附近徘徊，有可能还会往高处走。但是你的参数总体趋向于全局最小值附近徘徊。

随机梯度下降法的公式：

repeat {

 for J: 1 to m {

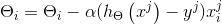
( for all i )

 }

}

表示对参数向量的，所有第i个位置按公式的方式进行更新。这个方法的好处是，修改参数时，仅需要查看第一个训练样本，并且利用第一个训练样本进行更新，之后使用第二个训练样本执行下一次更新。这样调整参数就会快很多。因为你不需要在调整之前，遍历所有的数据。