斯坦福公开课-机器学习2.监督学习应用-梯度下降（吴恩达 Andrew Ng）

Posted 2022-08-13 Wu_Being

文章目录

• 1线性代数（linear algebra）
• • 1-1 符号（Notation）
  • 1-2 例子——房价预测
  • 1-3 假设函数（hypothesis）
  • • 1-3-3 用`线性代数-非齐次方程`解释参数
    • • **1-普通梯度下降算法**
      • **2-批梯度下降算法（batch gradient descent algorithm）**
      • **3-随机梯度下降法（stochastic gradient descent）**
    • 1-4-2 最小二乘法

本系列课程链接

：http://open.163.com/special/opencourse/machinelearning.html

• 线性回归（linear regression）
• 梯度下降（gradient descent）
• 正规方程组（the normal equations）

1线性代数（linear algebra）

1-1 符号（Notation）

m 代表训练样本的数量，number of training examples；
x 代表输入变量或者特征（input variables/features），可以有多个；
y 代表输出变量或目标变量（output variable/target） ；
(x, y) 代表一个训练样本（one training example）；
i^th = (x⁽ⁱ⁾, y⁽ⁱ⁾) 表示第i个训练样本。

1-2 例子——房价预测

m = 47 个样本，每个样本有两个输入变量（**x₁**表示房子面积feet²，x₂表示房子卧室数目bedrooms），输出变量y表示房子价格。

1-3 假设函数（hypothesis）

h称为假设函数（hypothesis），接到输入，并输出结果，即将输入x映射到输出y。

###1-3-1 例子中的假设函数
h(x) = h_θ(x) = θ₀ + θ₁x₁ + θ₂x₂
###1-3-2 例子中的假设函数的参数
x₁表示房子面积size（或feet²），x₂表示房子卧室数目bedrooms。
n 表示学习问题中特征x的数目，这里的n为2。
θ Theta是算法参数（实数）一个三维变量 θ （θ₀, θ₁, θ₂），特征前面的参数（也称作特征权重），利用训练集合选择或学习，得到合适的参数值 θ （θ₀, θ₁, θ₂），是学习算法的任务，下面就讲求 θ值的方法。

1-3-3 用线性代数-非齐次方程解释参数

x₁，x₂：基础解系；
θ₁x₁ + θ₂x₂：通解；
θ₀：特解，为了简洁（conciseness）这里的特解定义为1。

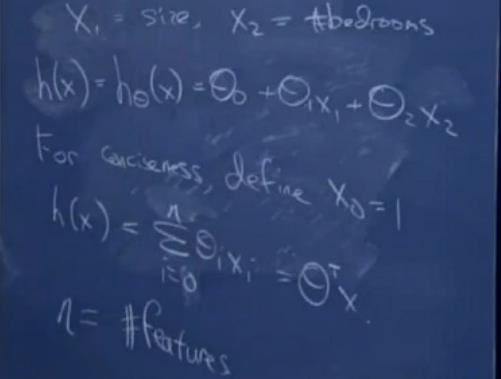
给定一些特征x以及一些正确的价格y，我们希望取使得算法预测和实际价格的平方差尽可能的小。
这里我们训练m样本求平方差的和最小，并为了后面方便导数计算就在前方乘以1/2，最后求值最小化minimize J(θ) 。
注意：这里为简化例子，把值最小化函数写成J(θ)，实际特征x的数目n是2， 原值最小化函数实际是J(θ₀, θ₁, θ₂)。

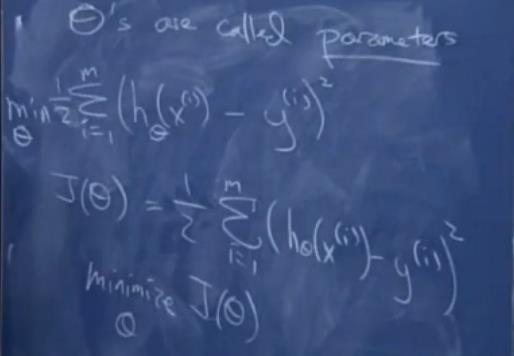
##1-4 求值最小化算法
###1-4-1 梯度下降算法（gradient descent algorithm）
我们先给参数向量初始化为一个0向量，然后不断地改变参数向量使得不断减少，直到取取最小值。我们称为梯度下降算法（gradient descent algorithm），也叫搜索算法（search algorithm）。

1-普通梯度下降算法

我们通过下面这个三维地表图来解释梯度下降算法（这里为方便绘画，我们令θ是二维向量，即(θ₀, θ₁)，函数的值J(θ)最小时，我们求得θ向量的值。）
当你站在某个初始点（即Theta θ可以是三维的0向量，也可以是随机的一个点）环视一周找哪个方向下山最快，就向那个方向走一步的大小（即 α的大小），再重复之前的动作再次梯度下降迭代下去，直到找到一个局部最小值（极小值点，局部最优值）。
当你在不同的初始点开始迭代这样的动作，可能会找到不同的局部最小值（如下图右部分），即梯度下降的结果有时依赖于参数的初始值。

[外链图片转存中…(img-C7kc7jsR-1652893852444)]

我们继续研究梯度下降的数学部分。我们在梯度下降过程每次起最陡的方向，就是把**θ_i**每次减去对应的偏微分值进行迭代更新。

θ_i := θ_i - α ∂(J(θ))/∂θ_i
注意：式子的i是对第i个参数进行迭代更新，即第i次下山，而不是第i个θ参数，因为θ**参数本来就是个三维变量。还有，我们用:=表示赋值，而=**表示逻辑判断相等。

其中α表示学习速率，即下山一步的大小，控制收敛的速度，过小则需要花费太多时间收敛，过大则可能会跳过最小值部分。
当你接近局部最小值的时候，步子会越来越小，最终直到收敛，当达到局部最小值的时候，梯度值也会为0，所以当越来越接近局部最小值的时候，梯度值也是越来越小，梯度下降的步子也会越来越小。

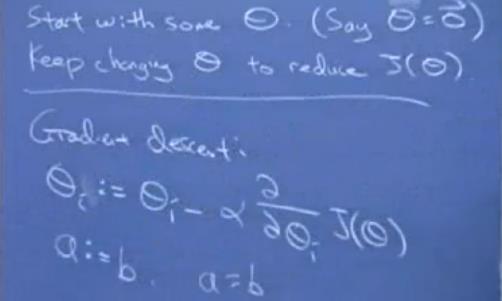
其中式子偏微分部分可以如下推导计算，最后梯度下降法为：
θ_i := θ_i - α （h_θ(x)-y）x_i
注意：式子的i是对第i个参数进行迭代更新，即第i次下山，不是第i个**θ_i**参数。

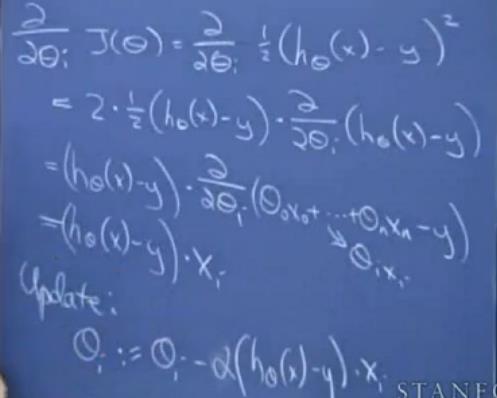
检测收敛的方法：比较两次迭代的结果，看两次结果是否变化很多，最常见的还是检测J(θ)函数的值，如果该值没有很大变化，则认为达到收敛的效果。
梯度下降算法中，计算的梯度(偏导)，事实上已经是梯度变化最大的方向。

2-批梯度下降算法（batch gradient descent algorithm）

对于多个样本，每次迭代都要遍历整个训练集合。

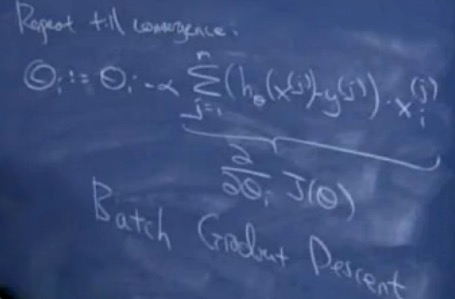
3-随机梯度下降法（stochastic gradient descent）

有时也称为增量梯度下降（incremental gradient descent），对大量数据集合的情况下，这个方法会快很多，但结果不会收敛到一个精确的值，而是向全局最小值徘徊。

1-4-2 最小二乘法

待完善…
#2正规方程组（the normal equations）
待完善…
#更多相关资料
梯度下降算法和正规方程组学习笔记：http://blog.csdn.net/hahajinbu/article/details/49904665
kaggle的比赛：http://www.kaggle.com
正规方程的推导过程：
https://zhuanlan.zhihu.com/p/22474562
AndrewNg - 线性回归【2】正规方程组：
http://blog.csdn.net/victor_gun/article/details/45268785
机器学习-线性回归-正规方程：
http://lib.csdn.net/article/machinelearning/35461
Wu_Being博客声明：本人博客欢迎转载，请标明博客原文和原链接！谢谢！
《【斯坦福公开课-机器学习】2.监督学习应用-梯度下降（吴恩达 Andrew Ng）》： http://blog.csdn.net/u014134180/article/details/76617963