01背包问题-只求背包的最终最大价值，不考虑选哪些物品怎么放---最优解(欢迎讨论)

Posted 2020-09-17 koliverpool

题目来自lintcode

http://www.lintcode.com/zh-cn/problem/backpack/

一个传统01背包问题的推广，假如只考一个背包放物品之后的最终最大价值，不考虑具体选哪些物品放入，该如何实现？

最蠢最笨的办法，那当然就是-老老实实的构造背包容量-物品矩阵，然后取出矩阵最上方最右的值即可：

代码也非常易懂：

class Solution:
    # @param m: An integer m denotes the size of a backpack
    # @param A: Given n items with size A[i]
    # @return: The maximum size
    def backPack(self, m, A):
        res=[[0 for i in range(len(A)+1)] for j in range(m+1)]
        for i in range(1,m+1):
            for j in range(1,len(A)+1):
                if A[j-1]>i:
                    res[i][j]=res[i][j-1]
                else:
                    res[i][j]=max(res[i][j-1],res[i-A[j-1]][j-1]+A[j-1])
        if len(res)>1:
            res=res[-2:]
        return res[-1][-1]

测试一下：

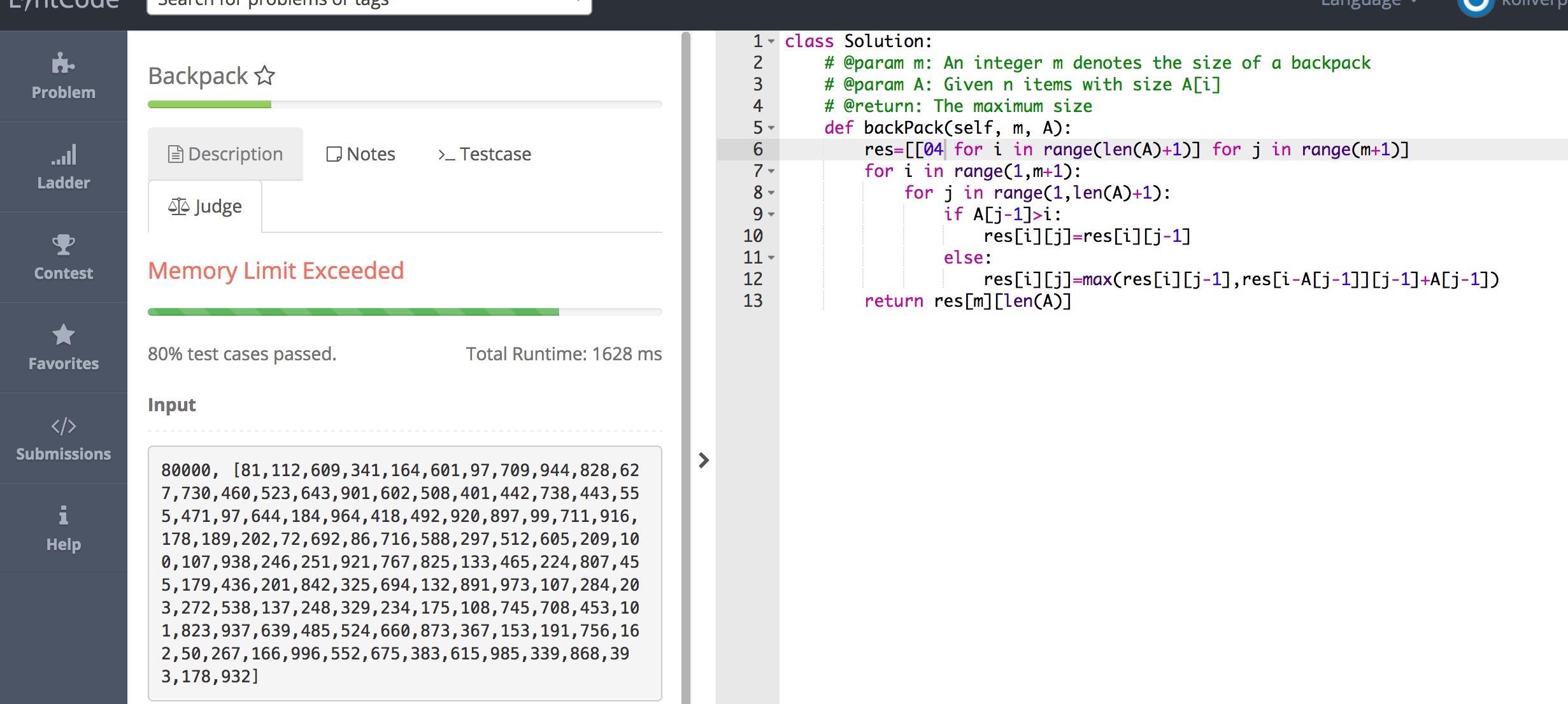
嗯哼，不炸内存才怪，显然这种解法，对于这个问题来说浪费太严重：

人家只要最终的最大值，不care怎么选，所以实际上只有最顶一行最后一个值是有用的，其他的都不需要。

所以我开始的思路是，就初始化两个长度为背包容量的数组，来回迭代，最后输出最后一次迭代的数组的最后一个值

自己改代码发现失败，代码是这么写的：

于是到群里问了七月的许老师，许老师说给你个C++的解法你改成python吧，她给的C++是这样：

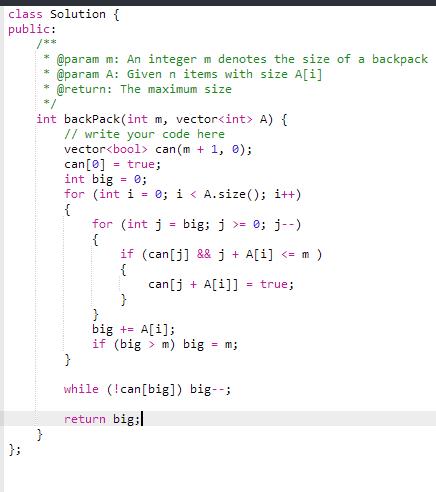
我改成了python，代码如下：

class Solution:
    # @param m: An integer m denotes the size of a backpack
    # @param A: Given n items with size A[i]
    # @return: The maximum size
    def backPack(self,m,A):
        can=[False for i in range(m+1)]
        can[0]=True
        big=0
        for i in range(len(A)):
            j=big
            while j>=0:
                if can[j] and j+A[i]<=m:
                    can[j+A[i]]=True
                j-=1
            big+=A[i]
            if big>m:
                big=m
        while can[big]==False:
            big-=1
        return big

嗯哼，牛逼了，3000ms顺利AC，但说实话这思路真的还没搞懂，写把代码贴在这儿，回头研究，欢迎各位博友给点思路，讨论一下~