cordic算法原理及verilog实现
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了cordic算法原理及verilog实现相关的知识，希望对你有一定的参考价值。
cordic算法原理及verilog实现
-
算法原理
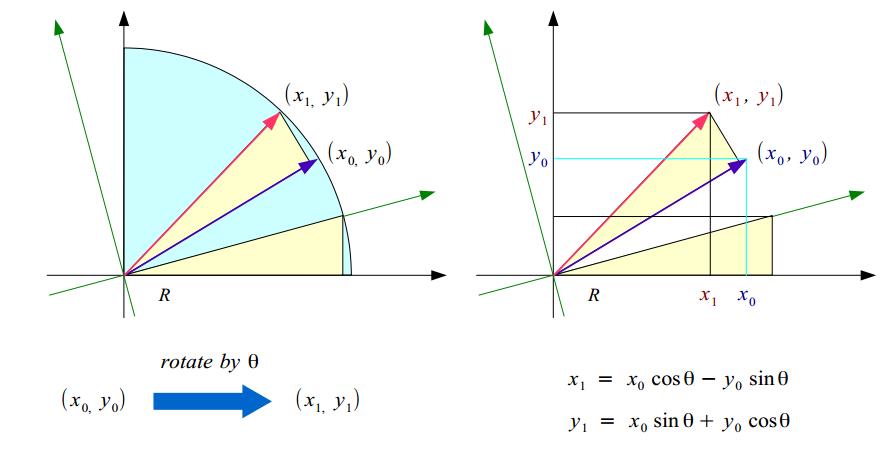
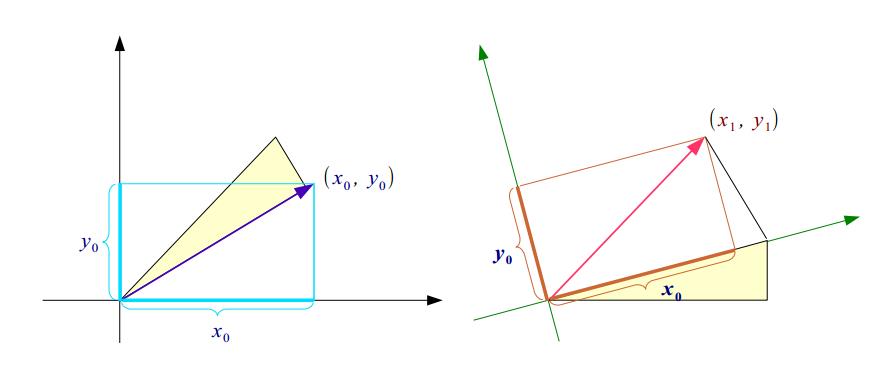
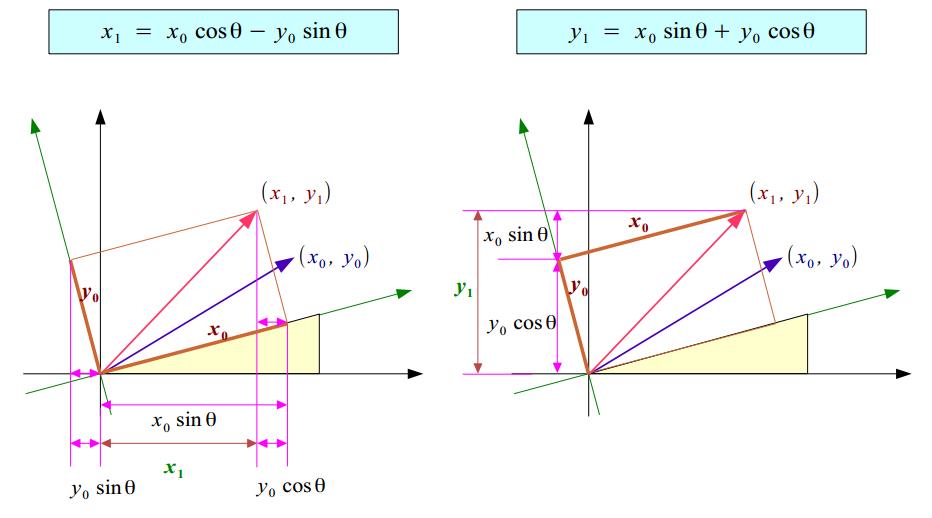
由此我们可以推出，当(x0,y0)与(x1,y1)的夹角为Θ时，满足如下关系：
由此可得，当(x1,y1)长度为1时，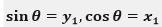
，当根据坐标旋转法旋转Θ角度后，坐标点变为(1,0)。因此，根据cordic算法求
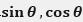就是将初始线段旋转至(1,0)后，所得的(x,y)的值。
下面，我们将这些旋转步骤细化，看看每一步是如何工作的。
假设第n次旋转为顺时针旋转时，会得到如下结果：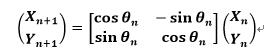
此时提取
会得到如下公式： 
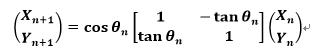
令每次旋转的角度Θ满足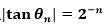
，则每次旋转最终的角度Θ满足：
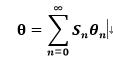，且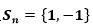
当顺时针旋转时
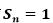，逆时针旋转时
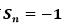。结合以上公式我们可以得到：
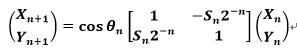因此每次迭代
都能提出来，最后他们的乘积是个常数K：
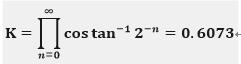
因此我们的计算过程是从点(1,0)开始，每次旋转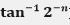
角度，Xn与Yn每次只需做移位运算即可。最终当
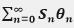等于Θ时，所得到的
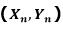即为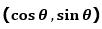
。 -
基于FPGA的算法设计
采用十六位补码的形式来表示输入角度和输出结果。输入角度采用角度制。十六位补码形式为：第一位表示符号位，第二位到第九位共八位表示整数位，第十位到第十六位共七位表示小数位。
采用十六级流水线的形式实现算法。每级流水线实现一次迭代。迭代开始之前需要先计算满足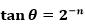
的Θ的值，并将他们转换成角度的表示形式存储起来作为中间变量。
在开始迭代之前，还要先将输入的角度转换为第一象限0-90度之间的角度进行迭代计算，并用一个flag位标识角度的正负。若为输入角度为负，则flag值为1，若角度为正，则flag值为0。此外还有九组临时变量x、y、z分别用来存储对应的横坐标、纵坐标以及剩余角度。
开始迭代之后，每次迭代都要根据cordic算法推出的公式计算x、y、z的值并将它们存储在中间变量中。
迭代完成之后，根据flag以及x8、y8的值计算最终的结果。如果flag值为1说明输入角度为负数，则将sinΘ等于(~y8+1)，否则sinΘ等于y8。无论flag值为多少，cosΘ均等与x8。 -
verilog代码实现
module cordic_2(rst,clk,datain,sin,cos);
input rst,clk;
input[15:0] datain;
output[15:0]sin,cos;
reg[15:0]sin,cos;
parameter[15:0] rot1 = 16‘b0000110101001000,
rot2 = 16‘b0000011100101110,
rot3 = 16‘b0000001110010000,
rot4 = 16‘b0000000111001010,
rot5 = 16‘b0000000011100101,
rot6 = 16‘b0000000001110011,
rot7 = 16‘b0000000000111001,
rot0 = 16‘b0001011010000000;
//parameter[15:0] k = 16‘b0000000001001110;
parameter[15:0] k = 16‘h004d;
reg[15:0] x0,y0,z0;
reg[15:0] x1,y1,z1;
reg[15:0] x2,y2,z2;
reg[15:0] x3,y3,z3;
reg[15:0] x4,y4,z4;
reg[15:0] x5,y5,z5;
reg[15:0] x6,y6,z6;
reg[15:0] x7,y7,z7;
reg[15:0] x8,y8,z8;
reg flag0,flag1,flag2,flag3,flag4,flag5,flag6,flag7,flag8;
//initial
always @(posedge clk or negedge rst)
begin
if(!rst)
begin
x0 <= 0;
y0 <= 0;
z0 <= 0;
flag0 <= 0;
end
else if(datain == 0)
begin
x0 <= 0;
y0 <= 0;
z0 <= 0;
flag0 <= 0;
end
else
begin
x0 <= k;
y0 <= 0;
if(datain[15])
z0 <= ~(datain-1);
else
z0 <= datain;
flag0 <= datain[15];
end
end
//1
always @(posedge clk or negedge rst)
begin
if(!rst)
begin
x1 <= 0;
y1 <= 0;
z1 <= 0;
flag1 <= 0;
end
else
begin
// if(z0[15])
// begin
// x1 <= x0 + y0;
// y1 <= x0 - y0;
// z1 <= z0 + rot0;
// flag1 <= flag0;
// end
// else
// begin
x1 <= x0 - y0;
y1 <= x0 + y0;
z1 <= z0 - rot0;
flag1 <= flag0;
// end
end
end
//2
always @(posedge clk or negedge rst)
begin
if(!rst)
begin
x2 <= 0;
y2 <= 0;
z2 <= 0;
flag2 <= 0;
end
else
begin
if(z1[15])
begin
x2 <= x1 + {y1[15],y1[15:1]};
y2 <= y1 - {x1[15],x1[15:1]};
z2 <= z1 + rot1;
flag2 <= flag1;
end
else
begin
x2 <= x1 - {y1[15],y1[15:1]};
y2 <= y1 + {x1[15],x1[15:1]};
z2 <= z1 - rot1;
flag2 <= flag1;
end
end
end
//3
always @(posedge clk or negedge rst)
begin
if(!rst)
begin
x3 <= 0;
y3 <= 0;
z3 <= 0;
flag3 <= 0;
end
else
begin
if(z2[15])
begin
x3 <= x2 + {{2{y2[15]}},y2[15:2]};
y3 <= y2 - {{2{x2[15]}},x2[15:2]};
z3 <= z2 + rot2;
flag3 <= flag2;
end
else
begin
x3 <= x2 - {{2{y2[15]}},y2[15:2]};
y3 <= y2 + {{2{x2[15]}},x2[15:2]};
z3 <= z2 - rot2;
flag3 <= flag2;
end
end
end
//4
always @(posedge clk or negedge rst)
begin
if(!rst)
begin
x4 <= 0;
y4 <= 0;
z4 <= 0;
flag4 <= 0;
end
else
begin
if(z3[15])
begin
x4 <= x3 + {{3{y3[15]}},y3[15:3]};
y4 <= y3 - {{3{x3[15]}},x3[15:3]};
z4 <= z3 + rot3;
flag4 <= flag3;
end
else
begin
x4 <= x3 - {{3{y3[15]}},y3[15:3]};
y4 <= y3 + {{3{x3[15]}},x3[15:3]};
z4 <= z3 - rot3;
flag4 <= flag3;
end
end
end
//5
always @(posedge clk or negedge rst)
begin
if(!rst)
begin
x5 <= 0;
y5 <= 0;
z5 <= 0;
flag5 <= 0;
end
else
begin
if(z4[15])
begin
x5 <= x4 + {{4{y4[15]}},y4[15:4]};
y5 <= y4 - {{4{x4[15]}},x4[15:4]};
z5 <= z4 + rot4;
flag5 <= flag4;
end
else
begin
x5 <= x4 - {{4{y4[15]}},y4[15:4]};
y5 <= y4 + {{4{x4[15]}},x4[15:4]};
z5 <= z4 - rot4;
flag5 <= flag4;
end
end
end
//6
always @(posedge clk or negedge rst)
begin
if(!rst)
begin
x6 <= 0;
y6 <= 0;
z6 <= 0;
flag6 <= 0;
end
else