Cordic,NCO基于Cordic算法的NCO的FPGA设计实现
Posted fpga&matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Cordic,NCO基于Cordic算法的NCO的FPGA设计实现相关的知识,希望对你有一定的参考价值。
1.软件版本
quartusii12.1
2.本算法理论知识
ROM资源,作为产生离散正弦信号的另一种有效途径,CORDIC(坐标旋转数值计算)算法已越来越受到青睐。其基本思想是通过一系列逐次递减的、与运算基数相关的往复偏摆以逼近最终需要达到的旋转角度。该算法仅利用加法和移位两种运算通过迭代方式进行矢量旋转, CORDIC算法由于只采用加法和移位运算,因此很适合在FPGA中实现,它可以用来实现数字下变频中的NCO、混频器和坐标变换等功能。
实现NCO的另一种方法是采用基于坐标旋转数字式计算机的算法,即CORDIC算法,基本思想是采用逐次逼近的方法实现三角函数的计算。该算法的突出优点是,仅做加减和移位运算,结合流水线,可以实现每一个时钟周期输出一个经过n次迭代的结果。


3.核心代码
module cordic_top(
i_clk,
i_reset,
i_phase_in,
o_sin_out,
o_cos_out
);
input i_clk; //?????
input i_reset; //???????
input [7:0]i_phase_in; //??????????
output[7:0]o_sin_out; //??
output[7:0]o_cos_out; //??
reg[7:0]reg_phase = 8'd0;
reg[7:0]o_sin_out = 8'd0;
reg[7:0]o_cos_out = 8'd0;
reg[7:0]x0 = 8'd0;
reg[7:0]y0 = 8'd0;
reg[7:0]z0 = 8'd0;
reg[7:0]x1 = 8'd0;
reg[7:0]y1 = 8'd0;
reg[7:0]z1 = 8'd0;
reg[7:0]x2 = 8'd0;
reg[7:0]y2 = 8'd0;
reg[7:0]z2 = 8'd0;
reg[7:0]x3 = 8'd0;
reg[7:0]y3 = 8'd0;
reg[7:0]z3 = 8'd0;
reg[7:0]x4 = 8'd0;
reg[7:0]y4 = 8'd0;
reg[7:0]z4 = 8'd0;
reg[7:0]x5 = 8'd0;
reg[7:0]y5 = 8'd0;
reg[7:0]z5 = 8'd0;
reg[7:0]x6 = 8'd0;
reg[7:0]y6 = 8'd0;
reg[7:0]z6 = 8'd0;
reg[7:0]x7 = 8'd0;
reg[7:0]y7 = 8'd0;
reg[7:0]z7 = 8'd0;
integer i;
reg[1:0]quadrant[8:0];
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
reg_phase <= 8'h00;
end
else begin
case(i_phase_in[7:8-2])
2'b00: reg_phase <= i_phase_in;
2'b01: reg_phase <= i_phase_in - 8'h40; //-pi/2
2'b10: reg_phase <= i_phase_in - 8'h80; //-pi
2'b11: reg_phase <= i_phase_in - 8'hc0; //-3pi/2
default:reg_phase <= 8'h00;
endcase
end
end
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
x0 <= 8'h00;
y0 <= 8'h00;
z0 <= 8'h00;
end
else begin
x0 <= 8'h4d;
y0 <= 8'h00;
z0 <= reg_phase;
end
end
//?????1?
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
x1<=8'b0000_0000;
y1<=8'b0000_0000;
z1<=8'b0000_0000;
end
else begin
if(z0[7]==1'b0)
begin
x1 <= x0 - y0;
y1 <= y0 + x0;
z1 <= z0 - 8'h20; //45deg
end
else begin
x1 <= x0 + y0;
y1 <= y0 - x0;
z1 <= z0 + 8'h20; //45deg
end
end
end
//?????2?
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
x2<=8'b0000_0000;
y2<=8'b0000_0000;
z2<=8'b0000_0000;
end
else begin
if(z1[7]==1'b0)
begin
x2 <= x1 - y1[7],y1[7:1];
y2 <= y1 + x1[7],x1[7:1];
z2 <= z1 - 8'h12; //26deg
end
else begin
x2 <= x1 + y1[7],y1[7:1];
y2 <= y1 - x1[7],x1[7:1];
z2 <= z1 + 8'h12; //26deg
end
end
end
//?????3?
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
x3<=8'b0000_0000;
y3<=8'b0000_0000;
z3<=8'b0000_0000;
end
else begin
if(z2[7]==1'b0)
begin
x3 <= x2 - 2y2[7],y2[7:2];
y3 <= y2 + 2x2[7],x2[7:2];
z3 <= z2 - 8'h09; //14deg
end
else begin
x3 <= x2 + 2y2[7],y2[7:2];
y3 <= y2 - 2x2[7],x2[7:2];
z3 <= z2 + 8'h09; //14deg
end
end
end
//?????4?
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
x4<=8'b0000_0000;
y4<=8'b0000_0000;
z4<=8'b0000_0000;
end
else begin
if(z3[7]==1'b0)
begin
x4 <= x3 - 3y3[7],y3[7:3];
y4 <= y3 + 3x3[7],x3[7:3];
z4 <= z3 - 8'h04; //7deg
end
else begin
x4 <= x3 + 3y3[7],y3[7:3];
y4 <= y3 - 3x3[7],x3[7:3];
z4 <= z3 + 8'h04; //7deg
end
end
end
//?????5?
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
x5<=8'b0000_0000;
y5<=8'b0000_0000;
z5<=8'b0000_0000;
end
else begin
if(z4[7]==1'b0)
begin
x5 <= x4 - 4y4[7],y4[7:4];
y5 <= y4 + 4x4[7],x4[7:4];
z5 <= z4 - 8'h02; //4deg
end
else begin
x5 <= x4 + 4y4[7],y4[7:4];
y5 <= y4 - 4x4[7],x4[7:4];
z5 <= z4 + 8'h02; //4deg
end
end
end
//?????6?
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
x6<=8'b0000_0000;
y6<=8'b0000_0000;
z6<=8'b0000_0000;
end
else begin
if(z5[7]==1'b0)
begin
x6 <= x5 - 5y5[7],y5[7:5];
y6 <= y5 + 5x5[7],x5[7:5];
z6 <= z5 - 8'h01; //2deg
end
else begin
x6 <= x5 + 5y5[7],y5[7:5];
y6 <= y5 - 5x5[7],x5[7:5];
z6 <= z5 + 8'h01; //2deg
end
end
end
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
for(i=0; i<=8; i=i+1)
begin
quadrant[i]<=2'b00;
end
end
else begin
for(i=0; i<8; i=i+1)
begin
quadrant[i+1] <= quadrant[i];
quadrant[0] <= i_phase_in[7:6];
end
end
end
always @(posedge i_clk or posedge i_reset)
begin
if(i_reset)
begin
o_sin_out <= 8'b0000_0000;
o_cos_out <= 8'b0000_0000;
end
else begin
case(quadrant[7])
2'b00:begin
o_sin_out <= y6;
o_cos_out <= x6;
end
2'b01:begin
o_sin_out <= x6;
o_cos_out <= ~(y6) + 1'b1;
end
2'b10:begin
o_sin_out <= ~(y6) + 1'b1;
o_cos_out <= ~(x6) + 1'b1;
end
2'b11:begin
o_sin_out <= ~(x6) + 1'b1;
o_cos_out <= y6;
end
default:begin
o_sin_out <= 8'b0000_0000;
o_cos_out <= 8'b0000_0000;
end
endcase
end
end
endmodule
4.操作步骤与仿真结论
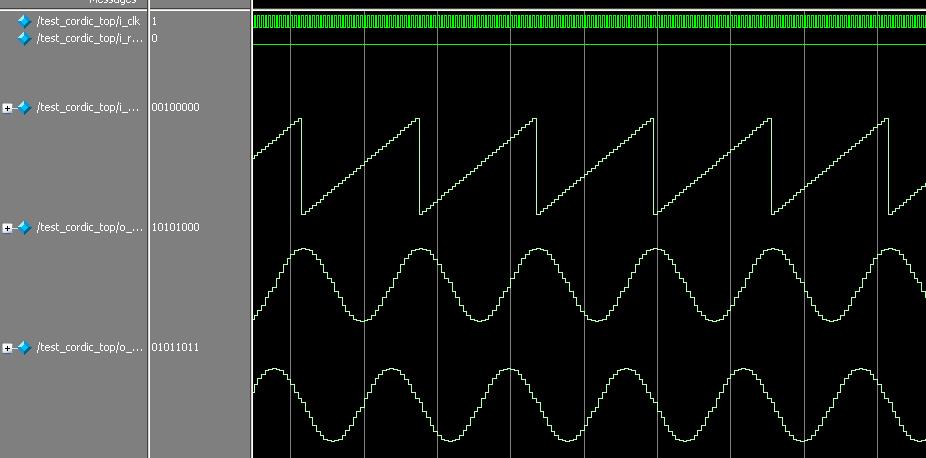
其RTL级的电路图如下所示:

从上面的仿真介绍可知,基于查找表的NCO,这种方式的固有特点决定了不仅需要大量的FPGA资源,而且混频器在实现过程中需要占用一定的乘法器资源,这对乘法器资源有限的FPGA而言很不利。
基于CORDIC算法的NCO,通过一系列固定的与运算基数相关的角度不断偏摆来逼近所需的旋转角度,其硬件结构简单,易于并行化处理。
5.参考文献
[1]朱涛玉,余志勇. 高效实现FPGA数字下变频的多类滤波器分组级联技术[J]. 现代电子技术, 2008, 31(23):4.
A01-115
6.完整源码获得方式
方式1:微信或者QQ联系博主
方式2:订阅MATLAB/FPGA教程,免费获得教程案例以及任意2份完整源码
以上是关于Cordic,NCO基于Cordic算法的NCO的FPGA设计实现的主要内容,如果未能解决你的问题,请参考以下文章