Exponential Distribution指数分布

Posted 2020-09-13

医药统计项目合作请联系

QQ：231469242

 

http://baike.baidu.com/item/%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83?sefr=cr

 

 

 

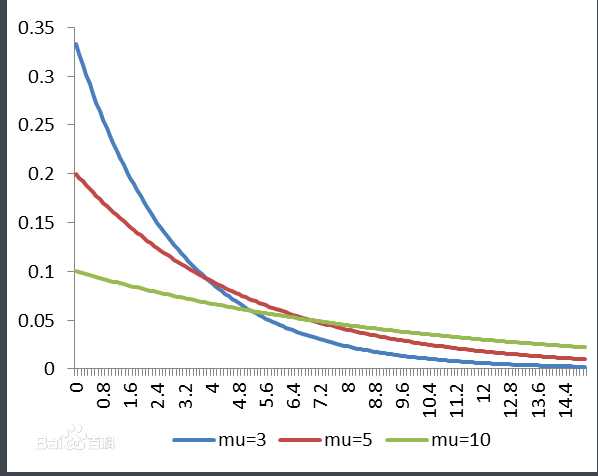
指数函数的一个重要特征是无记忆性（Memoryless Property，又称遗失记忆性）。这表示如果一个随机变量呈指数分布，当s,t>0时有P(T>t+s|T>t)=P(T>s)。即，如果T是某一元件的寿命，已知元件使用了t小时，它总共使用至少s+t小时的条件概率，与从开始使用时算起它使用至少s小时的概率相等。

记号

编辑

若随机变量x服从参数为λ的指数分布，则记为 X~ E(λ).

特性

编辑

无记忆性

指数函数的一个重要特征是无记忆性（Memoryless Property，又称遗失记忆性）。这表示如果一个随机变量呈指数分布

当s,t≥0时有P(T>s+t|T>t)=P(T>s)

即，如果T是某一元件的寿命，已知元件使用了t小时，它总共使用至少s+t小时的条件概率，与从开始使用时算起它使用至少s小时的概率相等。

分位数

率参数λ的四分位数函数（Quartile function）是：

F^-1(P;λ)= -LN(1-P)\\λ

第一四分位数：ln(4/3)\\λ

中位数： ln(2)\\λ

第三四分位数：ln(4)/λ

分布

编辑

在概率论和统计学中，指数分布（Exponential distribution）是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。

许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。指数分布是伽玛分布和威布尔分布的特殊情况，产品的失效是偶然失效时，其寿命服从指数分布。

指数分布可以看作当威布尔分布中的形状系数等于1的特殊分布，指数分布的失效率是与时间t无关的常数，所以分布函数简单。

应用

编辑

在电子元器件的可靠性研究中，通常用于描述对发生的缺陷数或系统故障数的测量结果。这种分布表现为均值越小，分布偏斜的越厉害。

指数分布应用广泛，在日本的工业标准和美国军用标准中，半导体器件的抽验方案都是采用指数分布。此外，指数分布还用来描述大型复杂系统（如计算机）的平均故障间隔时间MTBF 的失效分布。但是，由于指数分布具有缺乏“记忆”的特性．因而限制了它在机械可靠性研究中的应用，所谓缺乏“记忆”，是指某种产品或零件经过一段时间t0 的工作后,仍然如同新的产品一样,不影响以后的工作寿命值，或者说，经过一段时间t0的工作之后，该产品的寿命分布与原来还未工作时的寿命分布相同，显 然，指数分布的这种特性，与机械零件的疲劳、磨损、腐蚀、蠕变等损伤过程的实际情况是完全矛盾的，它违背了产品损伤累积和老化这一过程。所以，指数分布不 能作为机械零件功能参数的分布形式。

指数分布虽然不能作为机械零件功能参数的分布规律，但是，它可以近似地作为高可靠性的复杂部件、机器或系统的失效分布模型，特别是在部件或机器的整机试验中得到广泛的应用。

指数分布的图形表面上看与幂律分布很相似，实际两者有极大不同，指数分布的收敛速度远快过幂律分布。

指数分布的参数为λ，则指数分布的期望为1/λ，方差为(1/λ)的平方。