最小生成树——繁忙的都市

Posted 2020-09-10

题目描述

城市C是一个非常繁忙的大都市，城市中的道路十分的拥挤，于是市长决定对其中的道路进行改造。城市C的道路是这样分布的：城市中有n个交叉路口，有些交叉路口之间有道路相连，两个交叉路口之间最多有一条道路相连接。这些道路是双向的，且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值，分值越小表示这个道路越繁忙，越需要进行改造。但是市政府的资金有限，市长希望进行改造的道路越少越好，于是他提出下面的要求：

1．改造的那些道路能够把所有的交叉路口直接或间接的连通起来。

2．在满足要求1的情况下，改造的道路尽量少。

3．在满足要求1、2的情况下，改造的那些道路中分值最大的道路分值尽量小。

任务：作为市规划局的你，应当作出最佳的决策，选择那些道路应当被修建。

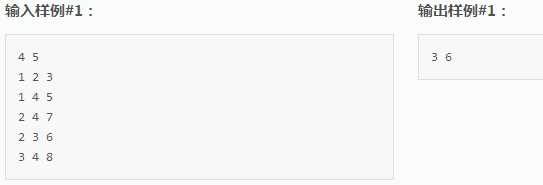
输入格式：

第一行有两个整数n,m表示城市有n个交叉路口，m条道路。接下来m行是对每条道路的描述，u, v, c表示交叉路口u和v之间有道路相连，分值为c。(1≤n≤300，1≤c≤10000)

输出格式： 

两个整数s, max，表示你选出了几条道路，分值最大的那条道路的分值是多少。

一道非常裸的最小生成树的题，然而交了四遍N/A才发现 memset 的函数库忘打了 TAT

输出的时候 s 直接输出路口数-1就可以了，因为n个点的连通图最少需要n-1条边，并且这道题只要输出最大的那个值，所以省去了累加求和，直接找出最大值就好了

prim代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m,map1[1000][1000],dis[1000];
bool pf[1000];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;
        map1[u][v]=w;
        map1[v][u]=w;
    }
    memset(dis,0x7f,sizeof(dis));    
    dis[1]=0;
     memset(pf,1,sizeof(pf));
    for(int i=1;i<=n;i++)
    {
        int k=0;
        for(int j=1;j<=n;j++)
        if(pf[j]&&dis[j]<dis[k]) k=j;
        pf[k]=0;
        for(int j=1;j<=n;j++)
        if(pf[j]&&map1[k][j]!=0&&map1[k][j]<dis[j]) 
        dis[j]=map1[k][j];
    }
    int o=-1;
    for(int i=1;i<=n;i++)
    if(dis[i]>o)
    o=dis[i];
    cout<<n-1<<" "<<o;
    return 0;
}

对了，郑某说我老是喜欢用prim，所以这道题我特意加了一种克鲁斯卡尔:

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int m,n,u,v,c,maxn,k;
int fa[301];
int find(int x) 
{
    if(fa[x]!=x) 
    fa[x]=find(fa[x]);
    return fa[x];
}
void unionn(int x,int y)
 {
    int fx=find(x);
    int fy=find(y);
    if(fx!=fy)fa[fx]=fy;
}
struct Node 
{
    int x, y, v;
    bool operator<(const Node &b)
    const
    {
        return v<b.v;
    }
}a[51000];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>u>>v>>c;
        a[i]=(Node){u, v, c};
    }
    for(int i=1;i<=n;i++) 
    fa[i]=i;
    sort(a+1,a+m+1);
    for(int i=1;i<=m;i++)
    {
        if(find(fa[a[i].x])!=find(fa[a[i].y])) 
        {
            unionn(a[i].x,a[i].y);
            maxn=a[i].v;
            k++;
        }
        if(k==n-1)break;
    }
    cout<<n-1<<" "<<maxn; 
    return 0;
}

以上代码基本上是模板，就懒得加注释了，各位看客自行脑补吧 (??ω??)