反应扩散方程与图灵图（世间万物神秘的斑图）

Posted 2020-08-17 尤是尤非

1952年，被后人称为计算机科学之父的著名英国数学家图灵(A．M．Turing)把他的目光转向生物学领域。他在著名论文“形态形成的化学基础”中nl，用一个反应扩散模型成功地说明了某些生物体表面所显示的图纹(如斑马身上的斑图)是怎样产生的 。 　　你或许会疑惑，斑马的条纹、猎豹的斑纹是怎样形成的等等，计算机之父图灵已经给我们明确的解释，或许我们可以从化学反应中得到一些启示，最经典的莫过于b-z反应了，这种反应扩散系统的随机性是其对称性遭到突破，也就是这种系统存在着失去稳定的情况。系统往往伴随着能量、物质的的反应与扩散。

　　1952年，被后人称为计算机科学之父的著名英国数学家图灵(A．M．Turing)把他的目光转向生物学领域。他在著名论文“形态形成的化学基础”中nl，用一个反应扩散模型成功地说明了某些生物体表面所显示的图纹(如斑马身上的斑图)是怎样产生的 。

　　你或许会疑惑，斑马的条纹、猎豹的斑纹是怎样形成的等等，计算机之父图灵已经给我们明确的解释，或许我们可以从化学反应中得到一些启示，最经典的莫过于b-z反应了，这种反应扩散系统的随机性是其对称性遭到突破，也就是这种系统存在着失去稳定的情况。系统往往伴随着能量、物质的的反应与扩散。

　　现在我试图使用计算机进行模拟，或许可以解决豹纹的形成过程。首先我使用的是gray-scott模型，

1. 反应扩散方程的一般形式:    
2. 

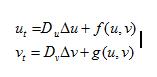
2.反应扩散方程式Gray-Scott 模型：

 3.对应的化学反应：

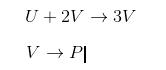
 4.好了，以上只是理论，哪里不懂的，上知网查文献，不在赘述。下面来讲计算机模拟的部分，，干货上了！！！注意了！！！

　　设计思想：反应物在U在两个V的作用下产生一个V，即U+2V->3V，会有中间产物P，当是P不参与反应过程。过程中U、V的浓度产生了不同的变化（扩散）。猎豹的体纹理就是在反应扩散过程中形成的 ，不同的大小其体纹理也随之不同。而gray-scott模型的扩散是在3X3的拉普拉斯方程列阵（不懂的自己查资料 ）中扩散的 。

　　编程：使用到OpenGL（不懂的看相关的书），纹理数组中的r、g、b像素扩散，每一次扩散都是在上一次扩散的基础上。每一个像素都有对应的U、V，UV就可以反映出这个像素的扩散情况。

1. 1. 1. 　　算法的核心：

         float A = a +
                  ((GS_Param.GS_DA*GS_Laplacian(x, y, GS_U)) -
                   (a*b*b) +
                   (GS_Param.GS_FEED*(1 - a)))*GS_DT;
         float B = b +
                 ((GS_Param.GS_DB*GS_Laplacian(x, y, GS_V)) +
                 (a*b*b) -
                  ((GS_Param.GS_KILL + GS_Param.GS_FEED)*b))*GS_DT;

         　　GS_Grid[x][y].a = fmin(fmax(A, 0), 1);
         　　GS_Grid[x][y].b = fmin(fmax(B, 0), 1);

         A：此时这个像素的U扩散情况；a：上一次U扩散值；GS_Laplacian（）拉普拉斯算子（网上查资料），B：此时这个像素的V扩散情况；b:上一次V扩散值；GS_Grid：各个像素点的数组（包含U、V）。

      2. 算法运用：

         float t = fmin(1, fmax(GS_Grid[i][j].a - GS_Grid[i][j].b, 0));
                     c = floor(t * 255);
         
         GS_Pix[i][j][0] = (GLubyte)c;
         GS_Pix[i][j][1] = (GLubyte)c;// floor(GS_Grid[i][j].a * 255);
          GS_Pix[i][j][2] = (GLubyte)c;// floor(GS_Grid[i][j].b * 255);
          GS_Pix[i][j][3] = (GLubyte)255;

         GS_Pix：像素数组，rgba（r,g,b,a）,表纹理如何设置纹理数组，请具体看计算机图形学的书籍。

      3. 实现效果：

                              

                              

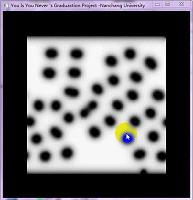
　　　　　　　　　　以上是还不同的供给量与扩散率的情况。

　　注意：

1、文章只是针对有OpenGL、c/c++编程和反应扩散系统基础的人，其他人可能比较难看懂。

2、其次，本文不提供完整的代码，代码归本博主所有。有问题请留言谢谢！

3、已发现有的网站盗用本文章却不标明为引用，欢迎举报到邮箱：[e-mail]；

4、文章原创地址：http://www.cnblogs.com/youyonggui/p/6703270.html