曲面曲率驱动的斑图传播

Posted 2022-12-07 陆嵩

曲面曲率驱动的斑图传播

前几天 PRL 杂志发布了一篇文章，是关于图灵斑图的。大概意思是说，对于在曲面的上斑图演化，受到曲面的形状的影响。这个 Letter 首次报告了在平面上的静态图灵斑图在曲面上是会传播的，而我们以往的研究里，都是假设图灵斑图在曲面上也是静态的。这篇文章研究了反对称曲面上的反应扩散系统。结果表明，曲面的对称性和斑图的样子都会影响斑图的传播。作者研究了曲面的曲率对斑图传播影响的一个机制。

一些研究已经表明了，当图灵斑图放到曲面上时，不稳定性条件是如何变化的，并且图案的位置如何受到曲面曲率的不均匀性的影响，这被称为 “pinning”。在这些研究中，总有一个前提假设，就是这些在平面上保持静止的图灵斑图在曲面上依然是保持静止的。但是这个假设条件的正确性并没有经过验证。

作者对图灵斑图模型 Brusselator 和 Lengyel-Epstein 做了一些数值验证。他们观察到，在平面上静止的斑图在一些曲面上发生了运动，他们给出了一些补充材料，包括两个视频说明这个问题，我把视频都转为了 gif，黏贴在下面。

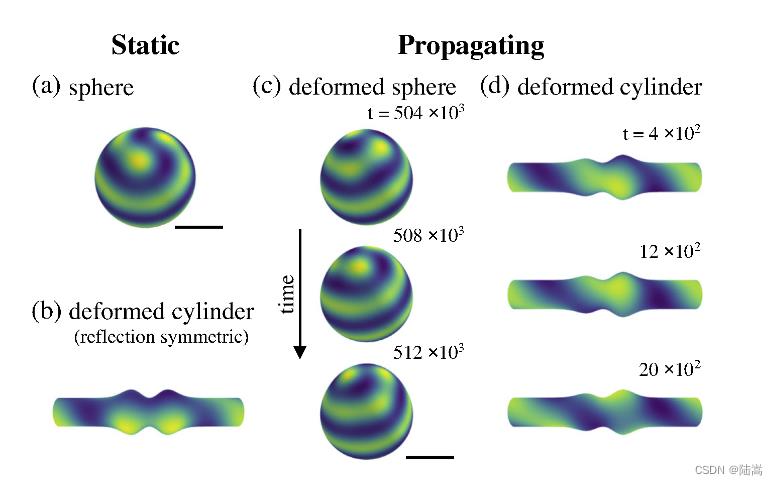
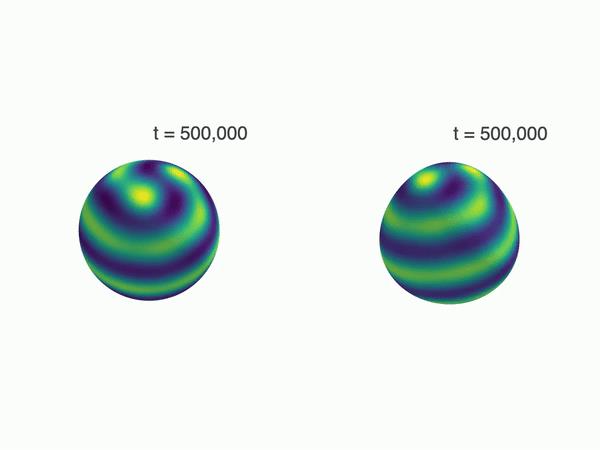
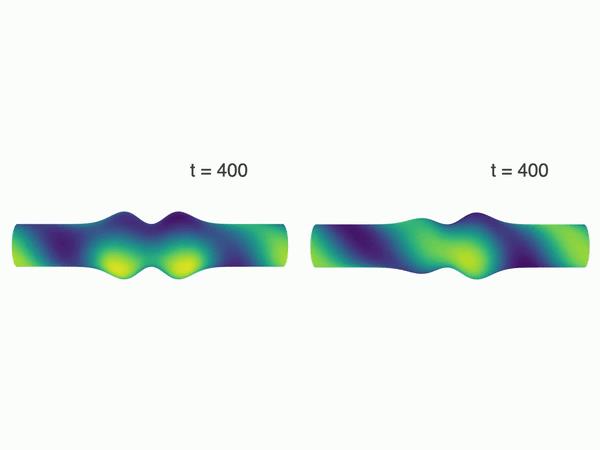
实验表明，曲率会导致图案的动态运动。研究结果表明曲面的对称性有助于图案的传播。比如说，图案在反射柱面上保持静止，在非反射的柱面上就开始运动。另外，在 Brusselator 和 LE 模型中都观察到了这种现象，说明这是一种通用的机制。

他们模拟了这样一个曲面，$r=[x,r(x)\cos \theta ,r(x)\sin \theta ]$，其中，$r(x)=d+k_1\cos (x)+k_2\cos (2x-\gamma \pi /2)$ ，$d=1.7,k_1=0.3$，$k_2=0.05$。这个模型中，如果$\gamma =0$就是轴对称的否则就不是轴对称的，如下图所示，

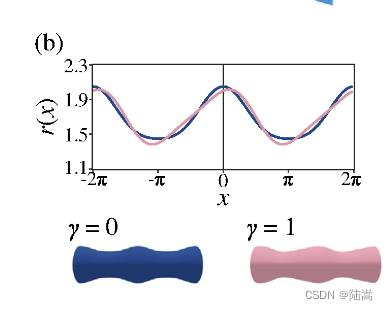
在一般的平面上，色散关系 $\mu (\lambda )$ 由线性不稳定分析得到，它表示了斑图的变化快慢，这里的 $\lambda$ 是曲面上拉普拉斯算子的特征值。事实上，这种色散关系在任何曲面上都是成立的。

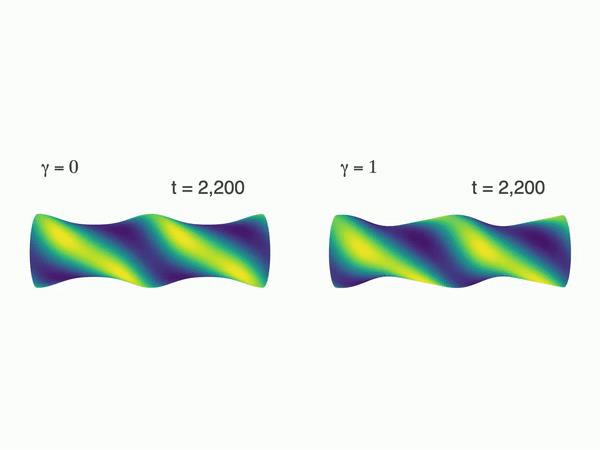
在上述的模型中，作者取不同的 $\gamma$ 参数，使得曲面的轴对称情况发生情况。结果表明，对称的曲面上 pattern 不会发生移动，非对称的曲面上会。如图：

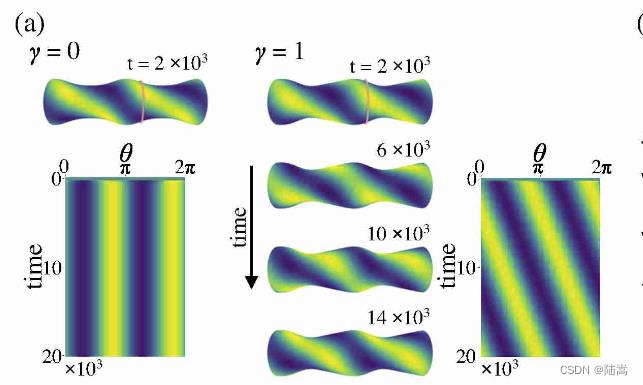
当然，作者的两个补充材料的两个视频也说明了这个问题。结果表明，轻微的反对称就能触发传播，反对称越明显，传播速度越快。调整参数和初始条件，可能还会出现平行于柱体的条纹，如图：

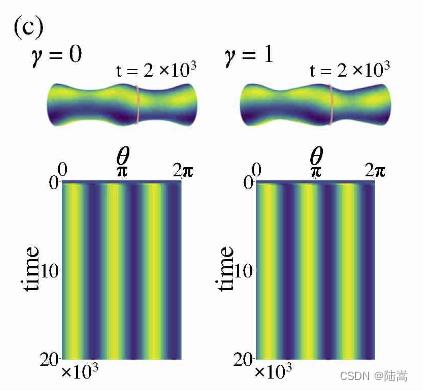
这种 pattern 形状下，我们就观察不到它的传播。点状的斑图，呈现出螺旋排列：

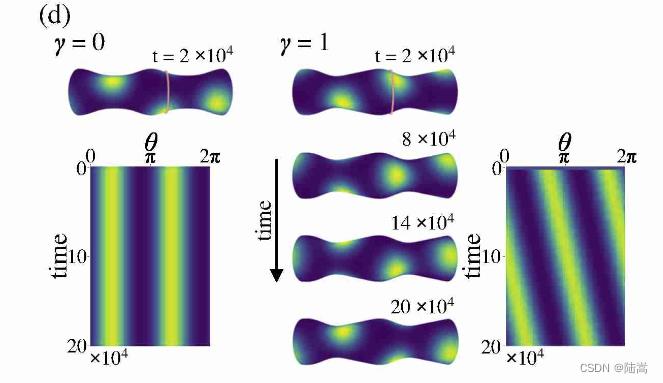
同样地，也可以平行于 x 轴，

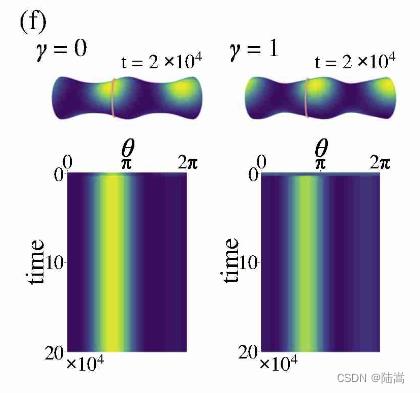
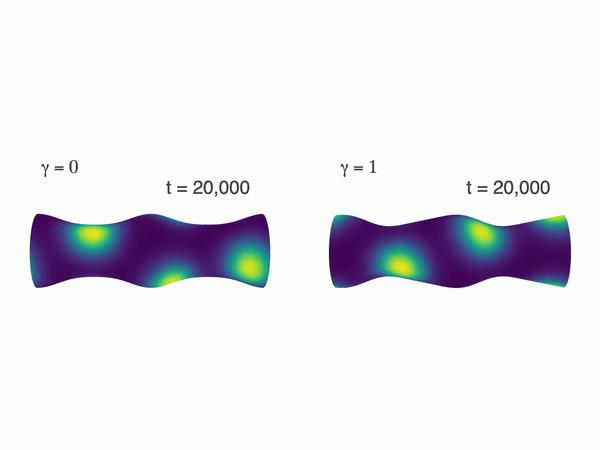
换不同的模型，不同的 pattern，都能得到相同的结论。即曲面是否对称以及初始班图的样子同时影响了 pattern 的传播。

作者还做了一些别的实验表明了了解的反对称性，是传播发生的关键。

根据上面得到的现象，作者从理论上进行了分析，表明了传播只能在非平衡态系统中发生。主要考虑的是如下的一个表达，
$$\omega =-\frac{\int dS{\partial }_{\rho }{\mathbf{U}}^T\mathbf{R}}{\int dS{\left({\partial }_{\rho }U\right)}^2}$$
这个表达式把曲面上 pattern 的传播速度和曲面的对称性以及pattern的初始形状联系起来了。反射对称时，这里的 $\omega =0$，pattern 也就不传播了。

为了搞清楚为什么对称性被打破了，pattern 就开始传播，作者做了所谓的扰动分析。这些分析刚好吻合了最前面的数值使用。

当然，上述的分析并没有排除高度对称的曲面上图案不对称带来的移动的问题。

总之，他们发现了真正由表面曲率驱动传播的化学波。这种传播不会发生在一维系统中，因为一维的情况下不存在实际意义的曲率，这与典型的传播波（例如在可激发介质中的传播波）形成对比，典型波的传播与表面几何形状无关。通过进行数值模拟和微扰分析，他们确定了 pattern 传播的一般条件，而与轴对称表面的模型方程无关，沿 x 轴的表面反射对称性丧失导致 pattern 的反
转对称性没了，故而 pattern 沿 θ 轴传播。表面和图案的（反）对称性都很重要，这表明在一般表面中，pattern 动力学由表面和 pattern 轮廓的几何特征决定。本文中发现的 pattern 传播以前被忽视了， 可能是因为以前的大多数研究主要集中在高度对称的表面上。此外，传播速度一般比早期pattern 形成要慢得多，所以很难直接观察到。

他们的研究结果暗示了表面几何对 pattern 动力学的新作用，这对工程和自然是有指导意义的。例如，在生长的器官中，表面的变形会导致波传播的启动（或抑制），这随后会导致器官生长的一个反馈调节。pattern 和表面几何形状之间的类似规律在细胞膜上的分子定位中也是可能发生的，无论是在表面内部还是外部。

本文只研究了稳定的曲面，在变化的曲面上可能也有类似的 pattern 移动的现象，那就更复杂了。
从视频中可以看得出来，虽然 pattern 在动，但是相对位置似乎是不变的，表现出来就是曲面一直在旋转。

参考文献：
Nishide R, Ishihara S. Pattern Propagation Driven by Surface Curvature[J]. Physical Review Letters, 2022, 128(22): 224101.